Свободная и несвободная точки
Материальная точка, движение которой в пространстве не ограничено какими-нибудь связями, называется свободной. Задачи решаются с помощью основного закона динамики.
Материальные точки, движение которых ограничено связями, называются несвободными.
Для несвободных точек необходимо определять реакции связей.
Эти точки движутся под действием активных сил и ограничивающих движение реакций связей (пассивных сил).
Несвободные материальные точки освобождаются от связей: связи заменяются их реакциями. Далее несвободные точки можно рассматривать как свободные (принцип освобождаемости от связей).
Сила инерции
Инертность - способность сохранять свое состояние неизменным, это внутреннее свойство всех материальных тел.
Сила инерции - сила, возникающая при разгоне или торможении тела (материальной точки) и направленная в обратную сторону от ускорения. Силу инерции можно измерить, она приложена к «связям» - телам, связанным с разгоняющимся или тормозящимся телом.
Рассчитано, что сила инерции равна

Таким образом, силы, действующие на материальные точки m1 и m 2
(рис. 14.1), при разгоне платформы соответственно равны

Разгоняющееся тело (платформа с массой m (рис. 2.1)) силу инерции не воспринимает, иначе разгон платформы вообще был бы невозможен.
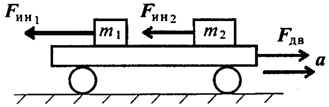
Рисунок 2.1
При вращательном движении (криволинейном) возникающее ускорение принято представлять в виде двух составляющих: нормального аn и касательного at (рис. 2.2)
Поэтому при рассмотрении криволинейного движения могут возникнуть две составляющие силы инерции: нормальная и касательная а = at + аn;
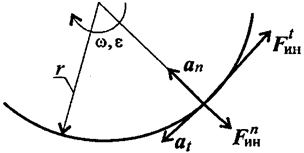
Рисунок 2.2
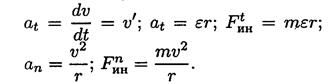
При равномерном движении по дуге всегда возникает нормальное ускорение, касательное ускорение равно нулю, поэтому действует только нормальная составляющая силы инерции, направленная по радиусу из центра дуги (рис. 2.3). ω = const;

Рисунок 2.3

Принцип кинетостатики (принцип Даламбера).
Принцип кинетостатики используют для упрощения решения ряда технических задач.
Реально силы инерции приложены к тепам, связанным с разгоняющимся телом (к связям).
Даламбер предложил Условно прикладывать силу инерции к активно разгоняющемуся телу. Тогда система сил, приложенных к материальной точке, становится уравновешенной, и можно при решении задач динамики использовать уравнения статики.
Принцип Даламбера:
Материальная точка под действием активных сил, реакций связей и условно приложенной силы инерции находится в равновесии:

Порядок решения задач с использованием принципа Даламбера:
1. составить расчетную схему;
2. выбрать систему координат;
3. выяснить направление и величину ускорения;
4. условно приложить силу инерции;
5. составить систему уравнений равновесия;
6. определить неизвестные величины.
Работа и мощность
Работа
Для характеристики действия силы на некотором перемещении точки ее приложения вводят понятие «работа силы».
Работа служит мерой действия силы, работа - скалярная величина.
Работа постоянной силы на прямолинейном пути
Работа силы в общем случае численно равна произведению модуля силы на длину пройденного пути и на косинус угла между направлением силы и направлением перемещения (рис. 3.1):

Рисунок 3.1

Единицы измерения работы:
1 Дж (джоуль)= 1 Н·м; 1 кДж (килоджоуль) = 103 Дж.
Рассмотрим частные случаи.
1. Силы, совпадающие с направлением перемещения, называются движущими силами. Направление вектора силы совпадает с направлением перемещения (рис. 3.2).
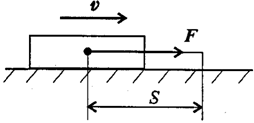
Рисунок 3.2
В этом случае 
2. Силы, пepпeндикуляpныe направлению перемещения, работы не производят (рис. 3.3).

Рисунок 3.3
Сила F перпендикулярна направлению перемещения. α = 90 º (cosα = 0); W = 0.
3. Силы, направленные в обратную от направления перемещения сторону, называются силами сопротивления (рис. 3.4).

Рисунок 3.4
Сила F направлена в обратную от перемещения S сторону.
В этом случае, α = 180º (cosα = = -1), следовательно, W = -FS < 0.
Движущие силы увеличивают модуль скорости,
силы сопротивления уменьшают скорость.
Таким образом, работа может быть положительной и отрицательной в зависимости от направления силы и скорости.
Работа постоянной силы на криволинейном пути.
Пусть точка М движется по дуге окружности и сила F составляет некоторый угол, а с касательной к окружности (рис. 3.5).

Рисунок 3.5
Вектор силы можно разложить на две составляющие:

Используя принцип независимости действия сил, определим работу, каждой из составляющих силы отдельно:

где 

Нормальная составляющая силы Fn всегда направлена перпендикулярно перемещению и, следовательно, работы не производит:

При перемещении по дуге обе составляющие силы разворачиваются вместе с точкой М. Таким образом, касательная составляющая силы всегда совпадает по направлению с перемещением.
Будем иметь: W(Ft) = Ftφr.
Касательную силу Ft обычно называют окружной силой. Работа при криволинейном пути - это работа окружной силы:

Произведение окружной силы на радиус называют вращающим моментом:

Работа силы, приложенной к вращающемуся телу, равна произведению вращающего момента на угол поворота:

Работа силы тяжести
Работа силы тяжести зависит только от изменения высоты и равна произведению модуля силы тяжести на вертикальное перемещение точки (рис. 3.6):
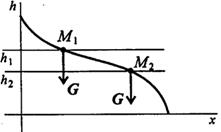
Рисунок 3.6
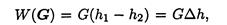
где Δh - изменение высоты.
При опускании работа положительна, при подъеме отрицательна.
Работа равнодействующей силы
Под действием системы сил точка массой G перемещается из положения М1 в положение М2 (рис. 3.7).
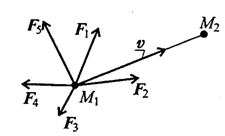
Рисунок 3.7
В случае движения под действием системы сил пользуются теоремой о работе равнодействующей.
Работа равнодействующей на некотором перемещении равна алгебраической сумме работ системы сил на том же перемещении.
FΣ = F1 + F2 + F3 + ... + Fn.
Работа равнодействующей силы

Работа и мощность.
Коэффициент полезного действия, мощность
Для характеристики работоспособности и быстроты совершения работы введено понятие мощности.
Мощность - работа, выполненная в единицу времени:
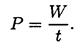
Единицы измерения мощности ватты и киловатты

Мощность при поступательном движении (рис. 16.1)
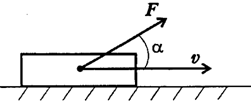
Рисунок 4.1

Учитывая, что

получим

где F - модуль силы, действующей на тело; Vcp - средняя скорость движения тела.
Средняя мощность при поступательном движении равна произведению модуля силы на среднюю скорость перемещения и на косинус угла между направлениями силы и скорости.
Мощность при вращении (рис.4.2)

Рисунок 4.2
Тело движется по дуге радиуса r из точки М1 В точку М2.
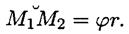
Работа силы 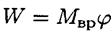
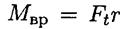
Где Mвр - вращающий момент

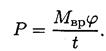
Учитывая, что получим 
где ωср - средняя угловая скорость
Мощность силы при вращении равна произведению вращающего момента на среднюю угловую скорость.
Если при выполнении работы усилие машины и скорость движения меняются, можно определить мощность в любой момент времени, зная значения усилия и скорости в данный момент.
Коэффициент полезного действия
Каждая машина и механизм, совершая работу, тратит часть энергии на преодоление вредных сопротивлений.
Таким образом, машина (механизм) кроме полезной работы совершает еще и дополнительную работу.
Отношение полезной работы к полной работе или полезной мощности ко всей затраченной мощности называется коэффициентом полезного действия (КПД):
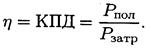
Полезная работа (мощность) расходуется на движение с заданной скоростью и определяется по формулам:

Затраченная мощность больше полезной на величину мощности, идущей на преодоление трения в звеньях машины, на утечки и тому подобные потери.
Чем выше КПД, тем совершеннее машина.
1.3 Примеры решения задач
Задача №3 Определить координаты центра тяжести составного сечения. Сечение состоит из листа и прокатных профилей (рис. 8.5)
Примечание.Часто рамы сваривают из разных профилей создавая необходимую конструкцию. Таким образом, уменьшается расход металла и образуется конструкция высокой прочности.
Для стандартных прокатных профилей собственные геометрические характеристики известны. Они приводятся в соответствующих стандартах.

Решение
1. Обозначим фигуры номерами и выпишем из таблиц необходимые данные:
1- швеллер N210 (ГОСТ 8240-89); высота h = 100мм; ширина полки Ь = 46мм; площадь сечения А1 = 10,9см2;
2 - двутавр № 16 (ГОСТ 8239-89); высота 160 мм; ширина полки 81 мм; площадь сечения А2 = 20,2см2;
3 - лист 5×100; толщина 5мм; ширина 100мм; площадь сечения А3 = 0,5 ·10 = 5см2
2. Координаты центров тяжести каждой фигуры можно определить по чертежу.
Составное сечение симметрично, поэтому центр тяжести находится на оси симметрии и координата Xс = 0.
Швеллер 1: Уl = а + h2 + ZO; Уl = 0,5 + 16 + 1,44 = 17,54см.
Двутавр 2: У2 = а + h2/2; У2 = 0,5 + 16/2 = 8,5 см. 2
Лист 3: У3 = а/2 = 0,25 см.
3. Определение центра тяжести составного сечения:

Дата добавления: 2019-01-14; просмотров: 1227; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
