Точка приложения силы тяжести
Для определения точки приложения силы тяжести (равнодействующей параллельных сил) используем теорему Вариньона о моменте равнодействующей:
Момент равнодействующей относительно оси равен алгебраической сумме моментов сил системы относительно этой оси.
 Изображаем тело, составленное из некоторых частей, в пространственной системе координат (рис. 8.2).
Изображаем тело, составленное из некоторых частей, в пространственной системе координат (рис. 8.2).
Тело состоит из частей, силы тяжести которых приложены в центрах тяжести (ЦТ) этих частей.
Пусть равнодействующая (сила тяжести всего тела) приложена в неизвестном пока центре С.
хс, УС и zс - координаты центра тяжести С.,
xk, Yk и zk - координаты центров тяжести частей тела.
 Из теоремы Вариньона следует:
Из теоремы Вариньона следует:

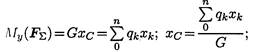
Аналогично для оси Oz:
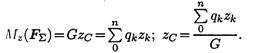
В однородном теле сила тяжести пропорциональна объему V:
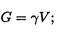
Где γ - вес единицы объема.
Следовательно, в формулах для однородных тел:

Где Vk - объем элемента тела; V - объем всего тела.
Центр тяжести однородных плоских тел (плоских фигур)
Очень часто приходится определять центр тяжести различных плоских тел и геометрических плоских фигур сложной формы. Для плоских тел можно записать:
V = Ah, где А - площадь фигуры, h - ее высота.
Тогда после подстановки в записанные выше формулы получим:
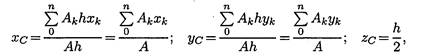
Где Ak - площадь части сечения; Xk, Yk - координаты ЦТ частей сечения.

Выражение называют статическим моментом площади (Sу)
Координаты центра тяжести сечения можно выразить через статический момент:
|
|
|

Оси, проходящие 'Через центр тяжести, называются центральными осями. Статический момент относительно центральной оси равен нулю.
Определение координат центра тяжести плоских фигур
Примечание. Центр тяжести симметричной фигуры находится на оси симметрии.
Центр тяжести стержня находится на середине высоты. Положения центров тяжести простых геометрических фигур могут быть рассчитаны по известным формулам (рис. 8.3: а) - круг; б) - квадрат, прямоугольник; в) - треугольник; г) - полукруг).

При решении задач используются следующие методы:
1) метод симметрии: центр тяжести симметричных фигур находится на оси симметрии;
2) метод разделения: сложные сечения разделяем на несколько простых частей, положение центров тяжести которых легко определить;
3) метод отрицательных площадей: полости (отверстия) рассматриваются как часть сечения с отрицательной площадью.
Кинематика
Кинематика точки
Анализ видов и кинетических параметров движений
Равномерное движение
Равномерное движение - это движение с постоянной скоростью:

Для прямолинейного равномерного движения (рис. 1.1а)

Рисунок 1.1


Полное ускорение движения точки равно нулю: а = 0.
|
|
|
При криволинейном равномерном движении (рис. 1.2)

Рисунок 1.2

Полное ускорение равно нормальному ускорению:
а = аn.
Уравнение (закон) движения точки при равномерном движении можно получить, проделав ряд несложных операций·
Так как v = const, закон равномерного движения в общем виде является уравнением прямой:
S = S0+vt,
где S0 - путь, пройденный до начала отсчета.
Равнопеременное движение
Равнопеременное движение - это движение с постоянным касательным ускорением:

Для прямолинейного равнопеременного движения

Полное ускорение равно касательному ускорению.
Криволинейное равнопеременное движение (рис. 10.2):


Учитывая, что и сделав ряд преобразований:

После интегрирования будем иметь закон равнопеременного движения в общем виде, представляющий уравнение параболы:

где Vo - начальная скорость движения;
S0 - путь, пройденный до начала отсчета; at - постоянное касательное ускорение.
Неравномерное движение
При неравномерном движении численные значения скорости и ускорения меняются.
Уравнение неравномерного движения в общем виде представляет собой уравнение третьей S = f ( t ³) и выше степени.
Кинематические графики
|
|
|
Кинематические графики - это графики изменения пути, скорости и ускорений в зависимости от времени.
Равномерное движение (рис. 1.3)

Рисунок 1.3
Равномерное движение (рис. 1.4)

Рисунок 1.4
Простейшие движения твердого тела
Поступательное движение
Поступательным называют такое движение твердого тела, при котором всякая прямая линия на теле при движении остается параллельной своему начальному положению (рис. 2.1, 2.2).
При поступательном движении все точки тела движутся одинаково: скорости и ускорения в каждый момент одинаковы. Поэтому для описания движения тела можно рассматривать движение одной его точки, обычно центра масс.
Поступательное движение может быть прямолинейным и криволинейным.

Рисунок 2.1
Вращательное движение
При вращательном движении все точки тела описывают окружности вокруг общей неподвижной оси.
Неподвижная ось, вокруг которой вращаются все точки тела, называется осью вращения.
При этом каждая точка движется по окружности, радиус которой равен расстоянию точки до оси вращения. Точки на оси вращения не перемещаются.
Для описания вращательного движения тела вокруг неподвижной оси можно использовать только угловые параметры (рис. 2.2):
|
|
|

Рисунок 2.2
φ- угол поворота тела, [φ] = рад;
ω - угловая скорость, определяет изменение угла поворота в единицу времени, [ω] = рад/с.
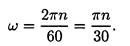
Изменение угловой скорости во времени определяется угловым ускорением ε, [ε] = рад/с²;
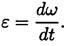
Частные случаи вращательного движения
Равномерное вращение (угловая скорость постоянна):

Уравнение (закон) равномерного вращения в данном случае имеет вид:

Где φ0 - угол поворота до начала отсчета.
Кинематические графики для этого вида движения изображены на рис. 2.3.

Рисунок 2.3
Равнопеременное вращение (угловое ускорение постоянно):
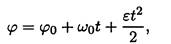
где ω0 - начальная угловая скорость.
Угловое ускорение при ускоренном движении - величина положительная угловая скорость будет все время возрастать.
Угловое ускорение при замедленном движении - величина отрицательная угловая скорость убывает.
Для данного движения кинематические графики представлены на рис. 2.4.

Рисунок 2.4
Скорости и ускорения точек вращающегося тела. Тело вращается вокруг точки о. Определим параметры движения точки А, расположенной на расстоянии rА от оси вращения (рис. 2.5, 2.6).

Рисунок 2.5

Рисунок 2.5
Путь точки А:

Линейная скopocть точки А:

Ускорения точки А:
 -касательное;
-касательное;
 -нормальное,
-нормальное,
где rА - радиус окружности, траектории точки А.
2. 4.3. Динамика
3. 4.3.1. Основные понятия и аксиомы динамики. Понятие о трении
Содержание и задачи динамики
Динамика- раздел теоретической механики, в котором устанавливается связь между движением тел и действующими на них силами.
В динамике решают два типа задач:
¾ определяют параметры движения по заданным силам;
¾ определяют силы, действующие на тело, по заданным кинематическим параметрам движения.
При поступательном движении все точки тела движутся одинаково, поэтому тело можно принять за материальную точку.
Если размеры тела малы по сравнению с траекторией, его тоже можно рассматривать как материальную точку, при этом точка совпадает с центром тяжести тела.
При вращательном движении тела точки могут двигаться не одинаково, в этом случае некоторые положения динамики можно применять только к отдельным точкам, а материальный объект рассматривать как совокупность материальных точек.
Поэтому динамику делят на динамику точки и динамику материальной системы.
Аксиомы динамики
Законы динамики обобщают результаты многочисленных опытов и наблюдений. Законы динамики, которые принято рассматривать как аксиомы, были сформулированы Ньютоном, но первый и четвертый законы были известны Галилею. Механику, основанную на этих законах, называют классической механикой.
Первая аксиома (принцип инерции)
Всякая изолированная материальная точка находится в состоянии покоя или равномерного и прямолинейного движения, пока приложенные силы не выведут ее из этого состояния.
Это состояние называют состоянием инерции. Вывести точку из этого состояния, т. е. сообщить ей некоторое ускорение, может внешняя сила.
Всякое тело (точка) обладает инертностью. Мерой инертности является масса тела.
Массой называют количество вещества в объеме тела, в классической механике ее считают величиной постоянной. Единица измерения массы - килограмм (кг).
Дата добавления: 2019-01-14; просмотров: 1966; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
