Задачи теоретической механики
Теоретическая механика - наука о механическом движении материальных твердых тел и их взаимодействии. Механическое движение понимается как перемещение тела в пространстве и во времени по отношению к другим телам, в частности к Земле.
Для удобства изучения теоретическую механику подразделяют на статику, кинематику и динамику.
Статика изучает условия равновесия тел под действием сил. Кинематикарассматривает движение тел как перемещение в пространстве; характеристики тел и причины, вызывающие движение, не рассматриваются. Динамика изучает движение тел под действием сил.
В отличие от физики теоретическая механика изучает законы движения некоторых абстрактных абсолютно твердых тел: здесь материалы, форма тел существенного значения не имеют. При движении абсолютно твердое тело не деформируется и не разрушается. 13 случае, когда размерами тела можно пренебречь, тело заменяют материальной точкой. Это упрощение, принятое в теоретической механике, значительно облегчает решение задач о движении.
Понятие о силе и системе сил.
Сила - это мера механического взаимодействия материальных тел между собой.
Взаимодействие характеризуется величиной и направлением, т. е. сила есть величина векторная, характеризующая точкой приложения (А), направлением (линией действия), величиной (модулем) (рис. 1.1).
Силу измеряют в ньютонах,
Рисунок 1.1
1Н=1кг 
м/c2
|
|
|
Силы, действующие на теле (или систему тел), делятся на внешние и внутренние. Внешние сил бывают активные, и реактивные. Активные силы вызывают перемещение тела, реактивные стремятся противодействовать перемещению тела под действием внешних сил.
Внутренние силы возникают в теле под действием внешних сил.
Совокупность сил, действующих на какое-либо тело, называют системой сил.
Эквивалентная система сил - система сил, действующая так же, как заданная.
Уравновешенной (эквивалентной нулю) системой сил называется такая система, которая, будучи приложенной, к телу, не изменяет его состояния.
- Систему сил, действующих на тело, можно заменить одной равнодействующей, действующей так, как система сил.
Аксиомы статики
В результате обобщения человеческого опыта были установлены общие закономерности механического движения, выраженные в виде законов и теорем. Все теоремы и уравнения статики выводятся из нескольких исходных положений. Эти положения называют аксиомами статики.
Первая аксиома
Под действием уравновешенной системы сил абсолютно твердое тело или материальная точка находятся в равновесии или движутся равномерно и прямолинейно (закон инерции).
|
|
|
Вторая аксиома
Две силы, равные по модулю и направленные по одной прямой в разные стороны, уравновешиваются (рис. 1.2).
Рисунок 1.2
Третья аксиома
Не нарушая механического состояния тела, можно добавить или убрать уравновешенную систему сил (принцип отбрасывания системы сил, эквивалентной нулю) (рис. 1.3).
Рисунок 1.3
Четвертая аксиома (правило параллелограмма сил)
Равнодействующая двух сил, приложенных в одной точке, приложена в той же точке и является диагональю параллелограмма, построенного на этих силах как на сторонах (рис. 1.4).
Вместо параллелограмма можно построить треугольник сил: силы вычерчивают одну за другой в любом порядке; равнодействующая двух сил соединяет начало первой силы с концом второй.
Рисунок 1.4
Пятая аксиома
При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие (рис. 1.5).
Рисунок 1.5
Силы, действующие и противодействующие всегда приложены к разным телам, поэтому они не уравновешиваются.
Силы, с которыми два тела действуют друг на друга, всегда равны по модулю и направлены вдоль одной прямой в разные стороны.
Следствие из второй и третьей аксиом силу, действующую на твердое тело, можно перемещать вдоль линии ее действия (рис. 1.6).
|
|
|
Рисунок 1.6
Сила F приложена в точке А. Требуется перенести ее B точку В. Используя третью аксиому, добавим в точке В уравновешенную систему сил (F'; F"). Образуется уравновешенная по второй аксиоме система сил (F; F"). Убираем ее и получим в точке В силу F", равную заданной F.
Связи и реакции связей
Все законы и теоремы статики справедливы для свободного твердого тела.
Все тела делятся на свободные и связанные.
Свободные тела - тела, перемещение которых не ограничено.
Связанные тела - тела, перемещение которых ограничено другими телами.
Тела, ограничивающие перемещение других тел, называют связями.
Силы, действующие от связей и препятствующие перемещению, называют реакциями связей. Реакция связи всегда направлена с той стороны, куда нельзя перемещаться
Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).
Все связи можно разделить на несколько типов.
Связь - гладкая опора (без трения)
Рисунок 1.7
Реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре (рис. 1.7).
Гибкая связь (нить, веревка, трос, цепь) Груз подвешен на двух нитях
|
|
|
(рис. 1.8).
Рисунок 1.8
Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.
Жесткий стержень
На схемах стержни изображают толстой сплошной линией (рис. 1.9).
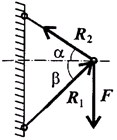
Рисунок 1.9
Стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи. Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допускается в данный момент наложенными на него связями. Убираем стержень 1, в этом случае стержень 2 падает вниз. Следовательно, сила от стержня 1 (реакция) направлена вверх. Убираем стержень 2. В этом случае точка А опускается вниз, отодвигаясь от стены. Следовательно, реакция стержня 2 направлена к стене.
Шарнирная опора
Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.
Подвижный шарнир
Стержень, закрепленный на шарнире, может поворачиваться вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки) (рис. 1.10).
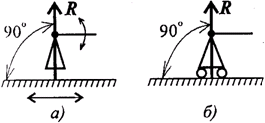
Рисунок 1.10
Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, т. к. не допускается только перемещение поперек опорной поверхности.
Неподвижный шарнир Точка крепления перемещаться не может. Стержень может свободно поворачиваться вокруг оси шарнира. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Ее принято изображать в виде двух составляющих: горизонтальной и вертикальной (Rx; Ry) (рис. 1.11).
Рисунок 1.11
Защемление или «заделка»
Любые перемещения точки крепления невозможны.
Под действием внешних сил в опоре возникают реактивная сила и реактивный момент MR, препятствующий повороту (рис.1.12).
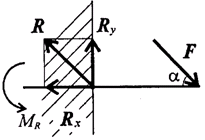
Рисунок 1.12
Реактивную силу принято представлять в виде двух составляющих вдоль осей координат
1. 4.1.2. Плоская система сходящихся сил.
Определение равнодействующей геометрическим способом
Плоская система сходящихся сил
Система сил, линии, действия которых пересекаются в одной точке, называется сходящейся (рис. 2.1).
Рисунок 2.1
Необходимо определить равнодействующую системы сходящихся сил
(F1; F2; Fз; Fn), n - число сил, входящих в систему.
По следствию из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными в одной точке.
Равнодействующая сходящихся сил.
Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма или треугольника сил (4-я аксиома) (рис. 2.2).
Рисунок 2.2
Используя свойства векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил (рис. 2.3). Вектор равнодействующей силы соединит начало первого вектора с концом последнего.
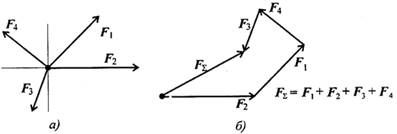
Рисунок 2.3
При графическом способе определения равнодействующей век торы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил - слагаемых. Такой способ получения равнодействующей называют геометрическим.
Замечание. При вычерчивании многоугольника обращать внимание на параллельность сторон многоугольника соответствующим векторам сил.
Порядок построения многоугольника сил:
1. вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпадал с началом последующего;
2. вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу;
3. при изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.
Условие равновесия плоской системы сходящихся сил.
При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.
Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.
Если в системе три силы, образуется треугольник сил. Сравните два треугольника сил (рис. 2.4) и сделайте вывод о количестве сил, входящих в каждую систему.
Рекомендация. Обратить внимание на направление векторов.
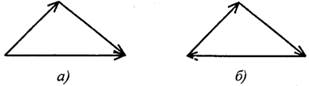
Рисунок 2.4
Определение равнодействующей аналитическим способом
Проекция силы на ось
Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца вектора (рис.3.1).
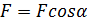
Рисунок 3.1
Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси. Таким образом, проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси (рис. 3.2).
Рисунок 3.2
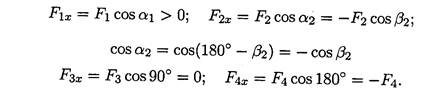
Проекция силы на две взаимноперпендикулярные оси (рис. 3.3).
Рисунок 3.3
Определение равнодействующей системы сил аналитическим способом
Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определяем равнодействующую геометрическим способом. Выберем систему координат, определим проекции всех заданных векторов на эти оси (рис. 3.4а). Складываем проекции всех векторов на оси X и Y (рис. 3.4б).
Рисунок 3.4
Модуль (величину) равнодействующей можно найти по известным проекциям:
Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующей с осями координат (рис. 3.5).
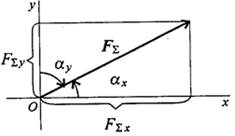
Рисунок 3.5
Условия равновесия плоской системы сходящихся сил в аналитической форме. Исходя из того, что равнодействующая равна нулю, получим:
Условия равновесия в аналитической форме можно сформулировать следующим образом:
плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы па любую ось равна нулю.
Система уравнений равновесия плоской сходящейся системы сил:
Пара сил и момент силы относительно точки
Пара сил, момент пары сил
Рисунок 4.1
Парой сил называется система двух сил, равных по модулю, параллельных и направленных в разные стороны.
Рассмотрим систему сил (F; F'), образующих пару.
Пара сил вызывает вращение тела, и ее действие на тело оценивается моментом. Силы, входящие в пару, не уравновешиваются, т. к. они приложены к двум точкам (рис. 4.1). Их действие на тело не может быть заменено одной силой (равнодействующей).
Момент пары сил численно равен произведению модуля силы на расстояние между линиями действия сил (плечо пары).
Момент считают положительным, если пара вращает тело по часовой стрелке (рис. 4.1б):
Плоскость, проходящая через линии действия сил пары, называется плоскостью действия пары.
Свойства пар (без доказательств):
1. Пару сил можно перемещать в плоскости ее действия.
2.Эквивалентность пар. Две пары, моменты которых равны, (рис. 4.2) эквивалентны (действие их на тело аналогично).
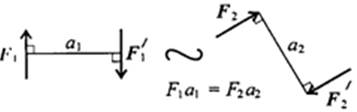
Рисунок 4.2
3. сложение пар сил. Систему пар сил можно заменить равнодействующей парой.
Момент равнодействующей пары равен алгебраической сумме моментов пар, составляющих систему (рис. 4.3):
Рисунок 4.3
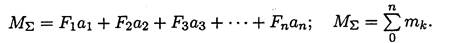
4. Равновесие пар.
Для равновесия пар необходимо и достаточно, чтобы алгебраическая сумма моментов пар системы равнялась нулю:
Момент силы относительно точки
Сила, не проходящая через точку крепления тела, вызывает вращение тела относительно точки, поэтому действие такой силы на тело оценивается моментом.
Момент силы относительно точки численно равен произведению модуля силы на расстояние от точки до линий действия силы.
Перпендикуляр, опущенный из точки на линию действия силы (рис. 4.4), называется плечом силы.
Рисунок 4.4
Обозначение момента mо(F) или mо(F);
Единица измерения
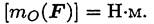
Момент считается положительным, если сила разворачивает тело по часовой стрелке.
Примечание. В разных учебных пособиях знак момента назначается по-разному.
Момент силы относительно точки равен нулю, если линия действия силы проходит через точку, т. к. В этом случае расстояние от точки до силы равно нулю.
Плоская система произвольно расположенных сил
Теорема Пуансо о параллельном переносе сил
Силу можно перенести параллельно линии ее действия, при этом нужно добавить пару сил с моментом, равным произведению модуля силы на расстояние, на которое перенесена сила.
Рисунок 5.1
Дано: сила в точке А (рис. 5.1).
Добавим в точке В уравновешенную систему сил (F'; F"). Образуется пара сил (F; F"). Получим силу в точке В и момент пары;
Приведение к точке плоской системы произвольно расположенных сил
Линии действия произвольной системы сил не пересекаются в одной точке, поэтому для оценки состояния тела такую систему следует упростить. Для этого все силы системы переносят в одну произвольно выбранную точку - точку приведения. Применяют теорему Пуансо. При любом переносе силы в точку, не лежащую на линии ее действия, добавляют пару сил.
Появившиеся при переносе пары называют присоединенными парами.
Дана плоская система произвольно расположенных сил (рис. 5.2). Переносим все силы в точку О. Получим пучок сил в точке О, который можно заменить одной силой - главным вектором системы. Образующуюся систему пар сил можно заменить одной эквивалентной парой - главным моментом системы.
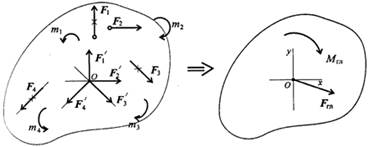
Рисунок 5.2
Главный вектор равен геометрической сумме векторов произвольной плоской системы сил. Проецируем все силы системы на оси координат и, сложив соответствующие проекции на оси, получим проекции главного вектора.
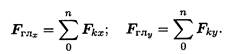
По величине проекций главного вектора на оси координат находим модуль главного вектора:
Главный момент системы сил равен, алгебраической сумме моментов сил системы относительно точки приведения.
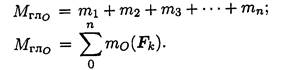
Таким образом, произвольная плоская система сил приводится к одной силе (главному вектору системы сил) и одному моменту (главному моменту системы сил).
Влияние точки приведения
Точка приведения выбрана произвольно. При изменении положения точки приведения величина главного вектора не изменится.
Величина главного момента при переносе точки приведения изменится, т. к. меняются расстояния от векторов сил до новой точки приведения.
С помощью теоремы Вариньона о моменте равнодействующей можно определить точку на плоскости, относительно которой главный момент равен нулю. Тогда произвольная плоская система сил может быть заменена одной силой. Эту силу называют равнодействующей системы сил. Численно равнодействующая равна главному вектору системы сил, но приложена в другой точке, относительно которой главный момент равен нулю. Равнодействующую принято обозначать F∑.
Численно ее значение определяется так же, как главный вектор системы сил:
Точку приложения равнодействующей можно определить по формуле
где d - расстояние от выбранной точки приведения до точки приложения равнодействующей;
Мгл - величина главного момента относительно выбранной точки приведения;
Fгл - величина главного вектора системы сил.
Частные случаи приведения системы сил к точке
При приведении системы сил к точке возможны следующие варианты:
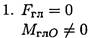=>тело вращается вокруг неподвижной оси..
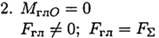=>тело движется прямолинейно ускоренно
=> тело находится в равновесии.
Условие равновесия произвольной плоской системы сил
1. При равновесии главный вектор системы равен нулю (Fгл = О).
Аналитическое определение главного вектора приводит к выводу:
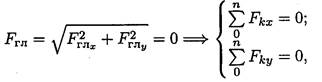
где Fkx и Fky - проекции векторов на оси координат.
2. Поскольку точка приведения выбрана произвольно, ясно, что при равновесии сумма моментов сил системы относительно любой точки на плоскости должна равняться нулю:
где А и В - разные точки приведения.
Условие равновесия произвольной плоской системы сил может быть сформулировано следующим образом:
Для того чтобы твердое тело под действием произвольной плоской системы сил находилось в равновесии, необходимо и до статочно, чтобы алгебраическая сумма проекций всех сил системы на любую ось равнялась нулю и алгебраическая сумма моментов всех сил системы относительно любой точки в плоскости действия сил равнялась нулю.
Получим основную форму уравнения равновесия:
уравнения моментов.
Теоретически уравнений моментов можно записать бесконечное множество, но практически доказано, что на плоскости можно составить только три независимых уравнения моментов и при этом три точки (центры моментов) не должны лежать на одной линии.
Таким образом, имеем пять независимых уравнений равновесия. Практически для решения задач на плоскости достаточно трех уравнений равновесия. В каждом конкретном случае используются уравнения с одним неизвестным.
Для разных случаев используются три группы уравнений равновесия.
Первая форма уравнений равновесия:
Вторая форма уравнений равновесия:
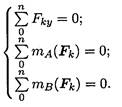
Третья форма уравнений равновесия:
Для частного случая, если уравновешена система параллельных сил, можно составить только два уравнения равновесия:
Ось Ох системы координат параллельна линии действия сил.
Балочные системы.
Определение реакций опор и моментов защемления
Виды нагрузок и разновидности опор
Виды нагрузок
По способу приложения нагрузки делятся на сосредоточенные и распределенные.
Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосредоточенной.
Часто нагрузка распределена по значительной площадке или линии (давление воды на плотину, давление снега на крышу и т. п.), тогда нагрузку считают распределенной.
В задачах статики для абсолютно твердых тел распределенную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 6.1).
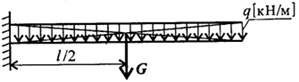
Рисунок 6.1
q - интенсивность нагрузки;
l - длина стержня;
G=q - равнодействующая распределенной нагрузки.
Балка - конструктивная деталь в виде прямого бруса, закреп ленная на опорах и изгибаемая приложенными к ней силами
Высота сечения балки незначительна по сравнению с длиной. Жесткая заделка (защемление) (рис. 6.2)
Рисунок 6.2
Каждое уравнение имеет одну неизвестную величину и решается без подстановок.
Для контроля правильности решений используют дополнительное уравнение моментов относительно любой точки на балке, например В:
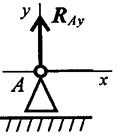
Рисунок 6.3
Шарнирно-подвижная опора (рис. 6.3) Опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности. Реакция направлена перпендикулярно опорной поверхности.
Шарнирно-неподвижная опора (рис. 6.4)
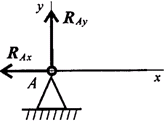
Рисунок 6.4
Опора допускает поворот вокруг шарнира и может быть заменена двумя составляющими силы вдоль осей координат.
Балка на двух шарнирных опорах (рис. 6.5)
Рисунок 6.5
Не известны три силы, две из них - вертикальные, следовательно, удобнее для определения неизвестных использовать систему уравнений во второй форме:
Составляются уравнения моментов относительно точек крепления балки. Поскольку момент силы, проходящей через точку крепления, равен 0, в уравнении останется одна неизвестная сила.
Из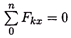 
уравнение определяется реакция Rвx
Из уравнения определяется реакция Rвy
Из уравнения определяется реакция RAy
Для контроля правильности решения используется дополнительное уравнение
При равновесии твердого тела, где можно выбрать три точки, не лежащие на одной прямой, удобно использовать систему уравнений в третьей форме (рис. 6.6):
Рисунок 6.6
Центр тяжести
Сила тяжести
Сила тяжести - равнодействующая сил притяжения к Земле, она распределена по всему объему тела. Силы притяжения, приложенные к частицам твердого тела, образуют систему сил, линии, действия которых сходятся в центре Земли (рис. 8.1). Поскольку ради ус Земли значительно больше размеров любого земного тела, силы притяжения можно считать параллельными.
Дата добавления: 2019-01-14; просмотров: 604; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!