Похідна функцій декількох змінних та деякі її застосування
Задача 5.1. Знайти для функції  частинні похідні першого порядку
частинні похідні першого порядку 
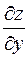 .
.
Розв’язання.
Обчислимо частинну похідну по змінній  .
.
 .
.
Тепер по  .
.

Задача 5.2. Знайти частинні похідні першого та другого порядку 
 ,
,  ,
,  ,
,  ,
,  для функції
для функції  .
.
Розв’язання.
Обчислимо частинні похідні першого порядку.
 ;
;
 .
.
Тепер обчислимо похідні другого порядку. При цьому врахуємо, що в силу теореми Шварца 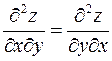 .
.
 ;
;
 ;
;
 .
.
Задача 5.3. Знайти похідну  функції
функції  , яку неявно задає рівняння
, яку неявно задає рівняння  .
.
Розв’язання.
Позначимо  .
.
• Похідна неявно заданої функції може бути обчислена за формулою
 .
.
Обчислимо частинні похідні.
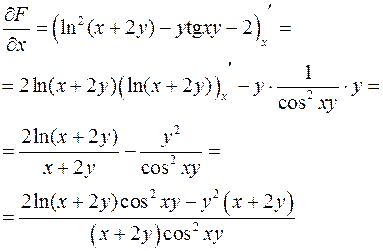


Тепер за формулою

Задача 5.4. Знайти похідну  показниково-степеневої функції
показниково-степеневої функції  .
.
Розв’язання.
Введемо нові змінні  , тоді задана функція набуде вигляду
, тоді задана функція набуде вигляду  .
.
• Для знаходження похідної цієї функції скористаємось формулою похідної складної функції:
 .
.
Для функції  :
:  . Далі знайдемо звичайні похідні
. Далі знайдемо звичайні похідні

Підставимо одержані вирази у формулу похідної складної функції.

Задача 5.5. Для функції  знайти градієнт у точці
знайти градієнт у точці  і похідну у цій точці за напрямом вектора
і похідну у цій точці за напрямом вектора  .
.
Розв’язання. За визначенням
• 
Знайдемо частинні похідні першого порядку:
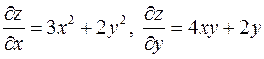 .
.
Обчислимо їх значення в точці  :
:

Тоді
 .
. 
• Похідна функції  за напрямком вектора
за напрямком вектора  дорівнює скалярному добутку
дорівнює скалярному добутку
 ,
,
де  – орт вектора
– орт вектора  .
.
Для заданого вектора знаходим
 .
.
Тоді
 .
.
Задача 5.6. Для заданої поверхні знайти рівняння дотичної площини і нормалі у точці М
1)  ;
;
2) 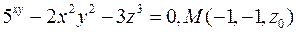 .
.
Розв’язання.
1)
• Для поверхні, яка задається рівнянням  , рівняння дотичної площини у точці
, рівняння дотичної площини у точці  має вигляд
має вигляд
 ,
,
а нормаль задається канонічним рівнянням виду
 .
.
Маємо з умови  . Значення функції
. Значення функції
 .
.
Обчислимо частинні похідні.


Тепер ми можемо записати рівняння дотичної площини.
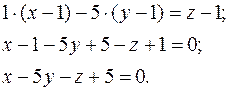
Рівняння нормалі:
 .
.
2)
• Для поверхні, яка задається рівнянням  рівняння дотичної площини у точці
рівняння дотичної площини у точці  має вигляд
має вигляд
 ,
,
а нормаль задається канонічним рівнянням виду
 .
.
Маємо з умови  . Значення функції знайдемо з рівняння
. Значення функції знайдемо з рівняння

Обчислимо частинні похідні.



Тепер ми можемо записати рівняння дотичної площини.

Рівняння нормалі:
 .
.
Задачі для самостійної роботи
1. Знайти частинні похідні першого та другого порядку 
 ,
,  ,
, 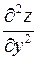 ,
,  ,
,  для заданої функції.
для заданої функції.
1)  2)
2)  3)
3)  .
.
4)  . 5)
. 5)  .
.
2. Знайти похідну 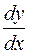 функції
функції  , яку неявно задає рівняння.
, яку неявно задає рівняння.
1)  . 2)
. 2)  .
.
3. Знайти похідну 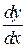 показниково-степеневої функції.
показниково-степеневої функції.
1)  . 2)
. 2) 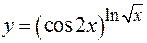 .
.
3)  .
.
4. Для функції  обчислити
обчислити  і
і  якщо
якщо 
5. Для функції 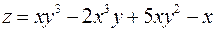 обчислити
обчислити 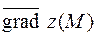 і
і 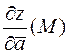 , якщо
, якщо  та
та  .
.
6. Для функції  обчислити
обчислити 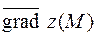 і похідну у точці
і похідну у точці 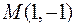 у напрямку найбільшого зростання функції у цій точці.
у напрямку найбільшого зростання функції у цій точці.
7. Скласти рівняння дотичної площини і нормалі до поверхні  у точці
у точці  .
.
8. Скласти рівняння дотичної площини і нормалі до поверхні  у точці
у точці  .
.
9. Скласти рівняння дотичної площини і нормалі до поверхні 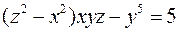 у точці
у точці 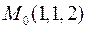 .
.
Екстремум функцій декількох змінних
Задача 5.7. Перевірити, чи являються точки  та
та  точками екстремуму функції
точками екстремуму функції  .
.
Розв’язання. Знайдемо частинні похідні першого порядку:
 ,
,  .
.
Оскількі похідні визначені при всіх значеннях  і
і  , то екстремуми можуть бути тількі у стаціонарних точках. Підставимо координати точки
, то екстремуми можуть бути тількі у стаціонарних точках. Підставимо координати точки  у частинні похідні.
у частинні похідні.
 ,
,  ,
,
значить точка М є стаціонарною точкою.
Для перевірки достатніх умов знайдемо частинні похідні другого порядку в точці М:  ,
,  ,
,  та обчислимо вираз
та обчислимо вираз 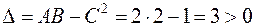 . Так як
. Так як  функція має у точці
функція має у точці  екстремум, причому, оскільки
екстремум, причому, оскільки 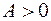 , то мінімум,
, то мінімум, 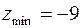 .
.
Тепер підставимо координати точки  у частинні похідні.
у частинні похідні.  ,
,  . Оскільки
. Оскільки  значить точка
значить точка  не є стаціонарною точкою, а, значить, не може бути точкою екстремуму.
не є стаціонарною точкою, а, значить, не може бути точкою екстремуму.
Задача 5.8. Дослідити функцію 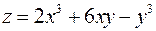 на екстремум.
на екстремум.
Розв’язання. Знайдемо частинні похідні першого порядку:
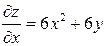 ,
,  .
.
Оскількі похідні визначені при всіх значеннях  і
і  , то екстремуми можуть бути тількі у стаціонарних точках. Знайдемо стаціонарні точки данної функції. Для цього розв’яжемо систему
, то екстремуми можуть бути тількі у стаціонарних точках. Знайдемо стаціонарні точки данної функції. Для цього розв’яжемо систему



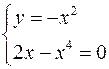 .
.
Звідки  ,
,  ,
,  ,
,  ,
, 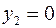 . Функція має дві стаціонарні точки:
. Функція має дві стаціонарні точки:  .
.
Для перевірки достатніх умов знайдемо частинні похідні другого порядку:
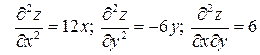 .
.
Обчислимо їх значення в точці  :
:
 .
.
Перевіримо достатні умови :
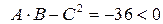 .
.
Отже, екстремуму в точці 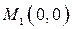 немає.
немає.
Для точки  :
:
 ;
;
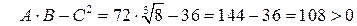 .
.
Отже, точка  є точкою мінімуму.
є точкою мінімуму.
Задача 5.9. Знайти найменше та найбільше значення функції  в області
в області 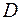 , яка обмежена заданими лініями
, яка обмежена заданими лініями  .
.
Розв’язання. Найбільше та найменше значення функції в замкнутій області знаходяться в точках екстремуму, що належать даній області, або на її межі. Таким чином, правило знаходження найбільшого та найменшого значень диференційованої в області  функції
функції 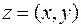 полягає у наступному:
полягає у наступному:
1) Знайти всі стаціонарні точки функції, що належать  , оскільки тільки в цих точках диференційована в області функція може мати екстремум. Потім обчислити в знайдених точках значення функції.
, оскільки тільки в цих точках диференційована в області функція може мати екстремум. Потім обчислити в знайдених точках значення функції.
2) Знайти найбільше та найменше значення функції 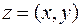 на границях області.
на границях області.
3) Порівняти всі знайденні значення функції та обрати з них найбільше М і найменше 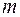 .
.
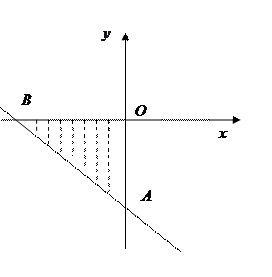 Зобразимо вказану область
Зобразимо вказану область  . Для цього знайдемо точки перетину прямих, що обмежують цю область. Граничні точки області:
. Для цього знайдемо точки перетину прямих, що обмежують цю область. Граничні точки області:  ,
,  ,
, 
Для знаходження усіх стаціонарних точок функції знаходимо частинні похідні:
 ,
, 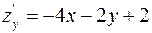 .
.
Оскільки похідні визначені в усіх точках області  , то екстремуми можуть бути тільки у стаціонарних точках. Для їх знаходження розв’яжемо систему рівнянь:
, то екстремуми можуть бути тільки у стаціонарних точках. Для їх знаходження розв’яжемо систему рівнянь:



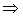


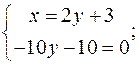



 .
.
Стаціонарна точка  не належить вказаній області, отже, значення функції в ній не береться до уваги. Далі дослідимо функцію на границі області
не належить вказаній області, отже, значення функції в ній не береться до уваги. Далі дослідимо функцію на границі області 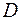 :
:
1) На відрізку 
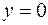 ,
,  .
.
Після підстановки  отримаємо функцію однієї змінної
отримаємо функцію однієї змінної  , яка досягає свого найбільшого (найменшого) значення на кінцях проміжку або в його стаціонарних точках. Знайдемо стаціонарні точки функції:
, яка досягає свого найбільшого (найменшого) значення на кінцях проміжку або в його стаціонарних точках. Знайдемо стаціонарні точки функції:
 ,
,  ,
,  .
.
Оскільки 
 , то знаходимо значення функції тільки на кінцях інтервалу:
, то знаходимо значення функції тільки на кінцях інтервалу:
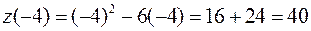 ,
,  .
.
2) На відрізку 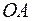

 .
.
Виконаємо вказану підстановку:  .
.
Знайдемо стаціонарні точки:
 ,
,  ,
,  .
.
Знаходимо значення функції на кінцях 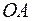 :
:
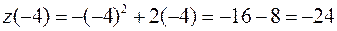 ,
, 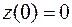 .
.
3) На відрізку 
 ,
,  .
.


 .
.
Знайдемо стаціонарні точки:
 ,
,  ,
, 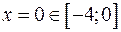 .
.
 ,
, 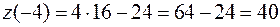 .
.
Отже,  – найбільше значення функції в області
– найбільше значення функції в області  ,
,  – найменше значення функції в області
– найменше значення функції в області 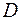 .
.
Задачі для самостійної роботи
1. Знайти точки екстремуму заданої функції.
1)  2)
2) 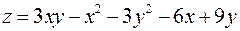
3)  4)
4) 
2. Знайти найменше та найбільше значення функції  в області
в області  , яка обмежена заданими лініями.
, яка обмежена заданими лініями.  .
.
3. Знайти найменше та найбільше значення функції  в області
в області  , яка обмежена заданими лініями.
, яка обмежена заданими лініями. 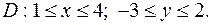
4. Знайти найменше та найбільше значення функції  в області
в області  , яка обмежена заданими лініями.
, яка обмежена заданими лініями. 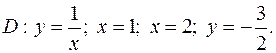
Дата добавления: 2018-11-24; просмотров: 210; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
