Похідна та деякі її застосування
Скласти рівняння площини, яка проходить через точку і пряму . 14. Скласти рівняння площини, яка проходить через точку перпендикулярно до прямої . 15. Визначити кут між прямою та площиною . 16. Перевірити перпендикулярність прямих 17. При яких значеннях і C пряма і площина перпендикулярні? 18. Обчислити відстань від точки до площини . 19. Визначити кут між двома площинами . 20. Скласти рівняння площини, яка проходить через точку паралельно площині . 21. Скласти рівняння площини, яка проходить через вісь та точку . 22. Скласти рівняння площини, яка проходить через точки , паралельно осі .
IV. Вступ до аналізу функцій однієї змінної
Границі
Задача 4.1. Обчислити границю
1)  ;
;
2)  .
.
Розв’язання.
1)


 .
.
2)
 .
.
У останньому дробі чисельник прямує до числа 5, а знаменник до нуля, тому дріб при  необмежено збільшується. В такому випадку кажуть, що границя дорівнює нескінченності.
необмежено збільшується. В такому випадку кажуть, що границя дорівнює нескінченності.
Задача 4.2. Обчислити границю  .
.
Розв’язання. Границя при  неперервної у точці
неперервної у точці  функції дорівнює значенню функції у цій точці. Оскільки всі елементарні функції неперервні на своїй області визначення, а функція під знаком границі є елементарною, то її границю можна знайти просто підставивши цю точку у функцію, при умові, що точка належить області визначення.
функції дорівнює значенню функції у цій точці. Оскільки всі елементарні функції неперервні на своїй області визначення, а функція під знаком границі є елементарною, то її границю можна знайти просто підставивши цю точку у функцію, при умові, що точка належить області визначення.
Підставимо  у функцію. Знаменник дробу при даному значенні дорівнює нулю, чисельник теж, отже
у функцію. Знаменник дробу при даному значенні дорівнює нулю, чисельник теж, отже  не належить області визначення функції, а значить знайти границю таким простим способом нам не вдасться. Більше того, якби чисельник не дорівнював нулю
не належить області визначення функції, а значить знайти границю таким простим способом нам не вдасться. Більше того, якби чисельник не дорівнював нулю  , ми могли б сказати, що границя дорівнює нескінченності, як у попередньому прикладі.
, ми могли б сказати, що границя дорівнює нескінченності, як у попередньому прикладі.
|
|
|
В нашому ж випадку ми зіткнулися з ситуацією, яку зазвичай позначають як  та називають невизначеністю. Подальші наші дії будуть направлені на розкриття невизначеності, яке буде полягати у скороченні дробу на вираз
та називають невизначеністю. Подальші наші дії будуть направлені на розкриття невизначеності, яке буде полягати у скороченні дробу на вираз  , тобто у нашому випадку на
, тобто у нашому випадку на  .
.
Для того, щоб скоротити дріб на  , ми розкладемо чисельник та знаменник на множники. У чисельнику для цього скористаємось формулою розкладання квадратного тричлена:
, ми розкладемо чисельник та знаменник на множники. У чисельнику для цього скористаємось формулою розкладання квадратного тричлена:
•  ,
,
де  – корені квадратного рівняння
– корені квадратного рівняння  .
.
В нашому випадку рівняння  має корені
має корені  , тому
, тому 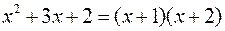 .
.
Для розкладення на множники знаменника виконаємо ділення многочленів „кутком”:

Таким чином  . Тепер наведемо обчислення границі:
. Тепер наведемо обчислення границі:
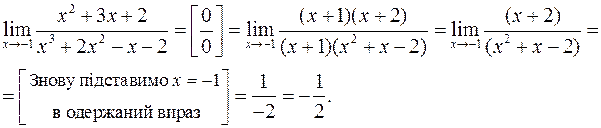
Задача 4.3. Обчислити границю
1)  ;
;
2)  .
.
Розв’язання.1)



2)




Задача 4.4. Обчислити границю  .
.
Розв’язання.

Задача 4.5. Обчислити границю
1)  ;
;
2)  .
.
Розв’язання.
1)


2)

Задача 4.6. Обчислити границю
1)  ;
;
2)  .
.
Розв’язання.
1)
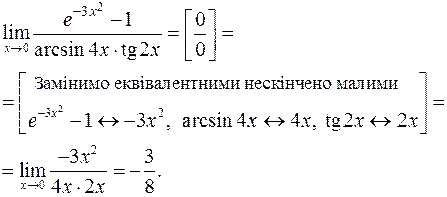
2)
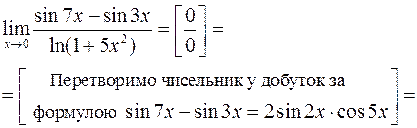

Задача 4.7. Знайти точки розриву функції та вказати їх тип
|
|
|

Розв’язання. Для дослідження на неперервність функції 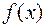 у точці
у точці  необхідно обчислити, по-перше, границю у цій точці справа
необхідно обчислити, по-перше, границю у цій точці справа  , по-друге, границю зліва
, по-друге, границю зліва  , по-третє, значення функції
, по-третє, значення функції 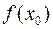 , якщо функція у точці визначена. Далі висновок можна зробити наступним чином:
, якщо функція у точці визначена. Далі висновок можна зробити наступним чином:
I. Якщо існують обидві скінчені границі, та
 ,
,
то точка  є точкою неперервності функції
є точкою неперервності функції  .
.
II. Якщо існують обидві скінчені границі, та
 ,
,
то точка  називається точкою усувного розриву (вважаємо що нерівність виконується і тоді, коли функція
називається точкою усувного розриву (вважаємо що нерівність виконується і тоді, коли функція  в точці
в точці  невизначена).
невизначена).
III. Якщо існують обидві скінчені границі та
 ,
,
то точка  називається точкою розриву першого роду.
називається точкою розриву першого роду.
IV. Якщо хоча б одна з границь 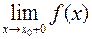 або
або 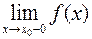 не існує (у тому числі є нескінченою), то точка
не існує (у тому числі є нескінченою), то точка  називається точкою розриву другого роду.
називається точкою розриву другого роду.
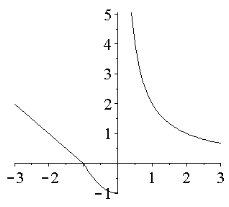
Оскільки кожна з трьох функцій справа від фігурної дужки є неперервною на відповідному інтервалі, то задана функція може мати розриви лише у точках  та
та  .
.
Дослідимо спочатку точку  . Маємо
. Маємо
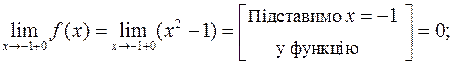
 та
та  .
.
Оскільки  , то точка
, то точка  є точкою неперервності функції.
є точкою неперервності функції.
Тепер дослідимо точку  . Маємо
. Маємо

 та
та  .
.
Оскільки одна з односторонніх границь  не існує, то точка
не існує, то точка  є точкою розриву другого роду.
є точкою розриву другого роду.
Зобразимо графік заданої функції на рисунку.
|
|
|
Задача 4.8. Знайти точки розриву функції та вказати їх тип
 .
.
Розв’язання. Точками розриву заданої функції можуть бути лише точки, які не входять в її область визначення, тобто точки, в яких знаменник дорівнює нулю. Розв’язуючи рівняння 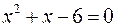 маємо корені
маємо корені  .
.
Дослідимо спочатку точку  . Маємо
. Маємо

Оскільки  , а у точці
, а у точці  функція невизначена, то точка
функція невизначена, то точка  є точкою усувного розриву функції.
є точкою усувного розриву функції.
Тепер дослідимо точку 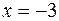 . Маємо
. Маємо
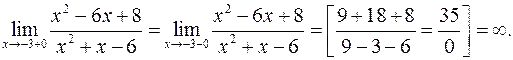
Оскільки односторонні границі  та
та  не існують, то точка
не існують, то точка  є точкою розриву другого роду.
є точкою розриву другого роду.
Задачі для самостійної роботи
1. Обчислити границі
1)  . 2)
. 2)  . 3)
. 3)  .
.
4)  . 5)
. 5) 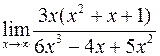 . 6)
. 6)  .
.
7)  . 8)
. 8)  . 9)
. 9)  .
.
10)  . 11)
. 11) 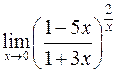 . 12)
. 12)  .
.
13)  . 14)
. 14)  . 15)
. 15)  .
.
16)  . 17)
. 17) 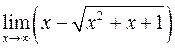 .
.
2. Знайти точки розриву функції та вказати їх тип. Зробити креслення.
1) 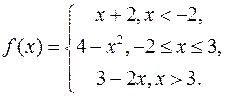 2)
2) 
3) 
3. Знайти точки розриву функції та вказати їх тип.
1) 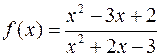 , 2)
, 2)  .
.
Похідна та деякі її застосування
Задача 4.9. Знайти похідну заданої функції
1)  ;
;
2) 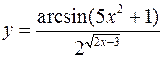 ;
;
3)  ;
;
4)  .
.
Розв’язання.
1)


2)
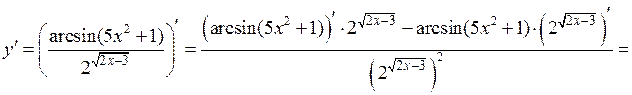
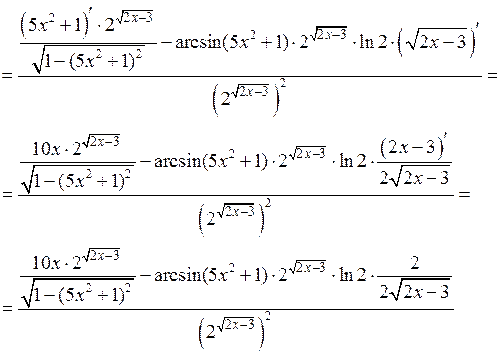
3)


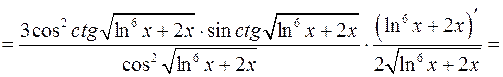


4)


Задача 4.10. Знайти похідні другого порядку 
1)  ;
;
2)  .
.
Розв’язання.
1) Обчислимо першу похідну.
|
|
|

Тепер обчислимо другу похідну.


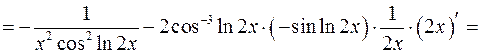

2)
• Обчислимо похідну параметрично заданої функції за формулою
 .
.
Маємо 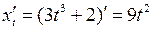 ,
,  .
.
Тобто 
• Тепер обчислимо другу похідну  за формулою
за формулою
 .
.
Тобто для нашої функції одержимо
 .
.
Задача 4.11. Знайти границі, застосувавши правило Лопіталя
1) 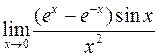 ;
;
2) 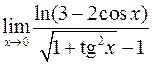 ;
;
3) 
Розв’язання.
1)
• Правило Лопіталя представляє собою наступну формулу
 ,
,
яка справедлива при умові, що в першій границі має місце одна із невизначеностей, які перелічені у квадратних дужках.
Проведемо обчислення заданої границі.



2)


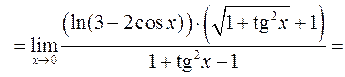



3) 
 .
.
Задача 4.12. Скласти рівняння дотичної та нормалі до графіка функції  в точці з абсцисою
в точці з абсцисою  .
.
Розв’язання.
• Рівняння дотичної до графіка функції  задається формулою
задається формулою  , де
, де 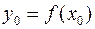 та
та  .
.
У нашій задачі  . Знайдемо похідну
. Знайдемо похідну
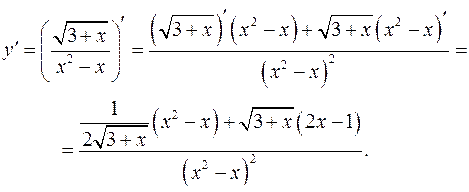
Тоді  .
.
Значить рівняння дотичної має вигляд

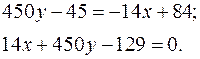
Нормаль – це пряма, яка проходить в заданій точці перпендикулярно до дотичної. Нормальний вектор дотичної  є напрямним для нормалі, відповідно для нормалі ми можемо записати канонічне рівняння у вигляді
є напрямним для нормалі, відповідно для нормалі ми можемо записати канонічне рівняння у вигляді
 .
.
Задача 4.13. Скласти рівняння дотичної та нормалі до кривої  у точці
у точці  .
.
Розв’язання.
Обчислимо  , та
, та  . Знайдемо похідну
. Знайдемо похідну
 .
.
Маємо  ,
, 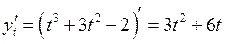 . Тобто
. Тобто 
Тоді 
Значить рівняння дотичної має вигляд

Нормаль – це пряма, яка проходить в заданій точці перпендикулярно до дотичної. Нормальний вектор дотичної  є напрямним для нормалі, відповідно для нормалі ми можемо записати канонічне рівняння у вигляді
є напрямним для нормалі, відповідно для нормалі ми можемо записати канонічне рівняння у вигляді
 .
.
Задачі для самостійної роботи
1. Обчислити похідні
1)  . 2)
. 2) 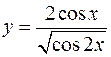 . 3)
. 3) 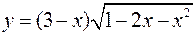 .
.
4)  . 5)
. 5)  . 6)
. 6)  .
.
7)  . 8)
. 8)  .
.
9)  . 10)
. 10) 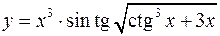 .
.
2. Знайти похідні другого порядку  .
.
1)  . 2)
. 2)  . 3)
. 3)  . 4)
. 4)  .
.
3. Знайти границі, застосувавши правило Лопіталя.
1)  . 2)
. 2)  .
.
3)  , 4)
, 4)  .
.
4. Скласти рівняння дотичної та нормалі до графіка функції  в точці з абсцисою
в точці з абсцисою  .
.
1)  . 2)
. 2)  .
.
5. Скласти рівняння дотичної та нормалі до кривої  у точці
у точці 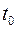 .
.
1)  . 2)
. 2)  .
.
Дата добавления: 2018-11-24; просмотров: 154; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
