Дослідження функцій та побудова їх графіків
Задача 4.14. Знайти найбільше та найменше значення функції 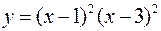 на відрізку
на відрізку  .
.
Розв’язання.
Якщо функція неперервна на замкненому відрізку, то свої найменше та найбільше значення вона приймає або в точках екстремуму, або на кінцях відрізку. Тому для знаходження найбільшого та найменшого значень функції ми знайдемо її критичні точки, після чого порівняємо значення функції у цих точках та на кінцях відрізку.
Спочатку обчислимо похідну.

Прирівняємо похідну до нуля.
 .
.
Це рівняння має корені  – критичні (стаціонарні) точки нашої функції. Перша з критичних точок
– критичні (стаціонарні) точки нашої функції. Перша з критичних точок 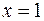 не належить заданому відрізку, тому її ми не розглядаємо. В інших критичних точках та на кінцях відрізку обчислимо значення функції.
не належить заданому відрізку, тому її ми не розглядаємо. В інших критичних точках та на кінцях відрізку обчислимо значення функції.

Отже найбільше значення функції  , а найменше –
, а найменше –  .
.
Задача 4.15. Провести повне дослідження функцій та побудувати їх графіки
1)  ;
;
2)  ;
;
3)  .
.
Розв’язання.
1)Дослідження функції здійснюється згідно наступної схеми:
а) Область визначення:  ;
;
б) Функція не є ні парною, ні непарною, так як  . Оскільки рівняння
. Оскільки рівняння  не має дійсних коренів, то графік функції не має точок перетину з віссю
не має дійсних коренів, то графік функції не має точок перетину з віссю  , але перетинає вісь
, але перетинає вісь  в точці (0,-1).
в точці (0,-1).
в) Точка розриву  , причому
, причому
 ;
;
 ,
,
отже, пряма  є вертикальною асимптотою графіка.
є вертикальною асимптотою графіка.
Знайдемо похилі асимптоти у вигляді  :
:

Таким чином, рівняння похилої асимптоти  .
.
г) Для знаходження точок екстремуму і проміжків монотонності обчислимо першу похідну функції:
|
|
|

Похідна визначена в усіх точках  , тому екстремум може бути тільки в стаціонарних точках. Їх знаходять з умови
, тому екстремум може бути тільки в стаціонарних точках. Їх знаходять з умови
 .
.
Так, точки  стаціонарні. Вони розбивають область визначення функції на інтервали
стаціонарні. Вони розбивають область визначення функції на інтервали  ,
, 
 причому
причому  на проміжках
на проміжках  та
та 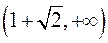 (функція зростає) і
(функція зростає) і 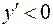 на проміжку
на проміжку  (функція спадає). Точки екстремуму:
(функція спадає). Точки екстремуму:
1) максимум при  , причому
, причому  ,
,
2) мінімум при  , причому
, причому 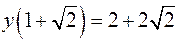 .
.
д) Визначимо інтервали опуклості, угнутості, а також точки перегину. Для цього знайдемо другу похідну:
 .
.
Так як  на проміжку
на проміжку  , то на ньому графік угнутий. При
, то на ньому графік угнутий. При 
 , отже, графік опуклий. Точок перегину нема, оскільки
, отже, графік опуклий. Точок перегину нема, оскільки  .
.
е) Використовуючи отримані дані, будуємо графік.


2) а) Область визначення функції:  .
.
б) Перевіримо парність функції:  . Отже, оскільки не виконуються ні рівність
. Отже, оскільки не виконуються ні рівність  , ані
, ані 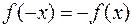 , то дана функція є функцією загального вигляду.
, то дана функція є функцією загального вигляду.
в) Знайдемо асимптоти графіка функції. Значення  є точкою розриву. При цьому
є точкою розриву. При цьому
 ,
,
 .
.
Тому  (вісь
(вісь  ) є вертикальною асимптотою.
) є вертикальною асимптотою.
Шукатимемо похилі асимптоти у вигляді  окремо при
окремо при 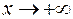 та при
та при  . При
. При  використаємо правило Лопіталя:
використаємо правило Лопіталя:
 , значить при
, значить при 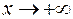 похилих асимптот немає.
похилих асимптот немає.
При 
 ,
,  ,
,
значить при 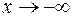
 – горизонтальна (оскільки
– горизонтальна (оскільки 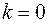 ) асимптота.
) асимптота.
г) Визначимо інтервали монотонності функції та наявність точок екстремуму. Обчислимо похідну та прирівняємо до нуля:
|
|
|
 ,
,  ,
,  .
.
Таким чином,  – критична точка функції. Ця точка розбила область визначення функції на інтервали:
– критична точка функції. Ця точка розбила область визначення функції на інтервали:  ,
, 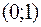 ,
,  . На кожному інтервалі
. На кожному інтервалі  зберігає знак, причому
зберігає знак, причому  на проміжках
на проміжках  ,
, 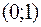 (функція зростає) і
(функція зростає) і 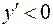 на проміжку
на проміжку  (функція спадає). При
(функція спадає). При  функція досягає мінімуму,
функція досягає мінімуму, 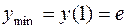 .
.
д) Далі визначимо інтервали опуклості та угнутості функції та точки перегину її графіку. Для цього обчислимо другу похідну та прирівняємо її до нуля.
 ,
,  .
.
Останнє рівняння дійсних коренів не має, тому точки перегину відсутні. Оскільки  при
при  , на цьому інтервалі графік функції опуклий, а при
, на цьому інтервалі графік функції опуклий, а при 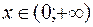 графік функції угнутий, тому що
графік функції угнутий, тому що  .
.
е) За результатами проведеного дослідження побудуємо графік функції

3) Виконаємо дослідження заданої функції.
а) Для знаходження області визначення розв’яжемо нерівність 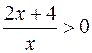 . Маємо область визначення:
. Маємо область визначення:  .
.
б) Функція не є ні парною, ні непарною, так як  . Для знаходження точок перетину графіка з віссю
. Для знаходження точок перетину графіка з віссю  розв’яжемо рівняння
розв’яжемо рівняння  . Одержуємо
. Одержуємо
 ,
,  ,
,  ,
,
значить графік функції перетинає вісь  у точці (–4,0). Графік не перетинає вісь
у точці (–4,0). Графік не перетинає вісь  , оскільки
, оскільки  не належить ОДЗ функції.
не належить ОДЗ функції.
в) Знайдемо вертикальні асимптоти. Для цього обчислимо
 ;
;  ,
,
отже, прямі  та
та  є вертикальними асимптотами графіка. Шукаємо похилі асимптоти у вигляді
є вертикальними асимптотами графіка. Шукаємо похилі асимптоти у вигляді  :
:
|
|
|

Таким чином, рівняння горизонтальної ( 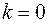 ) асимптоти
) асимптоти 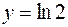 .
.
г) Для знаходження точок екстремуму і проміжків монотонності обчислимо першу похідну функції:

Похідна визначена в усіх точках з інтервалів  , тому екстремум може бути тільки в стаціонарних точках. Їх знаходимо з умови
, тому екстремум може бути тільки в стаціонарних точках. Їх знаходимо з умови
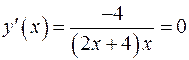 .
.
Дане рівняння розв’язків не має, відповідно не має і стаціонарних точок. Визначимо знак похідної. Одержимо, що  на всій області визначення нашої функції, отже функція спадає на кожному з проміжків
на всій області визначення нашої функції, отже функція спадає на кожному з проміжків  та
та  . Точок екстремуму функція не має.
. Точок екстремуму функція не має.
д) Визначимо інтервали опуклості, угнутості, а також точки перегину. Для цього знайдемо другу похідну:
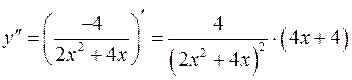 .
.
Прирівняємо похідну до нуля.
 .
.
Так як точка  не належить області визначення функції, точок перегину графік не має.
не належить області визначення функції, точок перегину графік не має.  на проміжку
на проміжку  , значить на цьому інтервалі графік угнутий. При
, значить на цьому інтервалі графік угнутий. При 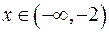
 , отже, графік опуклий.
, отже, графік опуклий.
е) Використовуючи отримані дані, будуємо графік.



Задачі для самостійної роботи
1. Знайти найбільше та найменше значення функції на відрізку.
1)  2)
2) 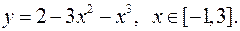
3)  4)
4) 
2. Провести повне дослідження функцій та побудувати їх графіки.
1) 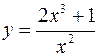 . 2)
. 2)  . 3)
. 3)  .
.
|
|
|
4) 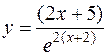 . 5)
. 5)  . 6)
. 6)  .
.
7)  .
.
V. Функції декількох змінних
Дата добавления: 2018-11-24; просмотров: 118; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
