Вероятность появления события в каждом из 100 независимых испытаний постоянна и равна 0,65. Найти вероятность того, что событие появится менее чем в половине случаев.
Решение:
 - число независимых испытаний;
- число независимых испытаний;  - вероятность появления события в одном испытании. Имеем схему Бернулли. Т.к. число испытаний велико, то вероятность появления события менее чем в половине случаев найдем по интегральной формуле Муавра-Лапласа:
- вероятность появления события в одном испытании. Имеем схему Бернулли. Т.к. число испытаний велико, то вероятность появления события менее чем в половине случаев найдем по интегральной формуле Муавра-Лапласа:  .
.
Найдем искомую вероятность:
 Ответ:
Ответ:  .
.
10. Среди шариков для подшипников 0,5% никелированы. Определить вероятность того, что в партии из 1000 шариков никелированных шариков будет 7 шт.
Решение:
Партия состоит из  шариков.
шариков.  - вероятность того, что шарик никелирован.
- вероятность того, что шарик никелирован.
Т.к. число испытаний велико, а вероятность мала, то для решения задачи воспользуемся формулой Пуассона:  , где
, где  .
.
 .
.
Искомая вероятность равна:
 .
.
Ответ:  .
.
Часть 2
ДСВ Х задана законом распределения

| -1 | 2 | 3 | 9 |

| 0,1 | 0,25 | 
| 0,15 |
Найти вероятность  , построить многоугольник распределения и функцию распределения.
, построить многоугольник распределения и функцию распределения.
Решение:
Найдем неизвестную вероятность  :
:
 .
.
Ряд распределения принимает вид:

| -1 | 2 | 3 | 9 |

| 0,1 | 0,25 | 0,5 | 0,15 |
Построим многоугольник распределения:

Найдем функцию распределения  :
:
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Функция распределения ДСВ Х имеет вид:
 .
.
Строим график  :
:

ДСВ Х задана законом распределения

| -1 | 2 | 3 | 9 |

| 0,1 | 0,25 | 0,5 | 0,15 |
Найти моду, математическое ожидание, дисперсию и среднеквадратическое отклонение ДСВ Х.
Решение:
Мода – это варианта с наибольшей вероятностью.
|
|
|
 .
.
Математическое ожидание:
 .
.
Дисперсия:
 .
.
Среднеквадратическое отклонение:
 .
.
В урне находится 3 белых и 7 черных шаров. Наудачу отобрано два шара. Найти математическое ожидание и дисперсию ДСВ Х – число белых шаров.
Решение:
Всего 10 шаров: 3 белых и 7 черных. Отбирают два шара.
ДСВ Х – число белых шаров, среди отобранных шаров. Составим ряд распределения ДСВ Х.
Х=0- среди отобранных шаров нет белых.
 ;
;
Х=1- среди отобранных шаров один белый шар.
 ;
;
Х=2- среди отобранных шаров два белых шара.
 ;
;
Ряд распределения ДСВ Х имеет вид:

| 0 | 1 | 2 |

| 
| 
| 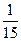
|
Математическое ожидание:
 .
.
Дисперсия:
 .
.
4. Задана плотность распределения НСВ Х  . Найти постоянную
. Найти постоянную  , функцию распределения и вероятность выполнения неравенства
, функцию распределения и вероятность выполнения неравенства 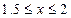 .
.
Решение:
Найдем неизвестный параметр  . По свойству плотности распределения вероятностей:
. По свойству плотности распределения вероятностей:  . Получаем:
. Получаем: 
 . Плотность распределения принимает вид:
. Плотность распределения принимает вид:  .
.
Найдем функцию распределения  .
.
 ;
;
 ;
;
 .
.
Функция распределения НСВ Х имеет вид:

Найдем вероятность выполнения неравенства 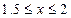 :
:
 .
.
5. Задана плотность распределения НСВ Х  . Определить начальные и центральные моменты НСВ первого и второго порядков.
. Определить начальные и центральные моменты НСВ первого и второго порядков.
|
|
|
Решение:
Начальный момент 1-го порядка:
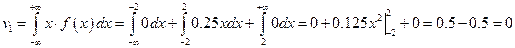
Начальный момент 2-го порядка:

Центральный момент 1-го порядка:
 .
.
Центральный момент 2-го порядка:

6. НСВ Х распределения по стандартному закону. Определить вероятность выполнения неравенства  .
.
Решение:
Т.к. НСВ Х распределена по стандартному закону то  , а
, а  .
.
Вероятность выполнения неравенства  найдем по формуле:
найдем по формуле:  .
.
Искомая вероятность равна:

Ответ: 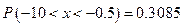 .
.
НСВ Х распределения по стандартному закону. Найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью 0,9973 попадает НСВ Х в результате испытания.
Решение:
Воспользуемся формулой:  .
.
Т.к. НСВ Х распределена по стандартному закону то  , а
, а  .
.
Найдем  . По условию задачи
. По условию задачи  .
.
 .
.
Длина интервала, симметричного относительно математического ожидания, в который с вероятностью 0,9973 попадает НСВ Х в результате испытания равна 3+3=6.
Ответ: 6.
8. НСВ Х распределена по показательному закону с параметром 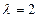 . Найти вероятность того, что в результате испытания НСВ Х примет значение лежащее в интервале (0,15;0,65).
. Найти вероятность того, что в результате испытания НСВ Х примет значение лежащее в интервале (0,15;0,65).
Решение:
Т.к. НСВ Х распределена по показательному закону с параметром 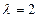 , то функция распределения этой НСВ имеет вид:
, то функция распределения этой НСВ имеет вид:
|
|
|
 .
.
Тогда вероятность того, что в результате испытания НСВ Х примет значение лежащее в интервале (0,15;0,65) равна:
 .
.
Ответ:  .
.
9. ДСВ Х имеет характеристики  и
и  . Оценить снизу вероятность события
. Оценить снизу вероятность события  .
.
Решение:
Для решение задачи воспользуемся неравенством Чебышева:  .
.

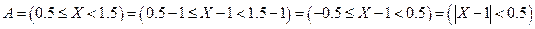 .
.
Считая  и используя неравенство Чебышева оценим снизу вероятность события
и используя неравенство Чебышева оценим снизу вероятность события  :
:
 .
.
Ответ:  .
.
10. Задана функция распределения двумерной СВ:  . Найти двумерную плотность распределения вероятности СВ.
. Найти двумерную плотность распределения вероятности СВ.
Решение:
Плотность распределения двумерной СВ найдем по формуле  .
.

 .
.
Ответ:  .
.
Мат статистика.
Дата добавления: 2018-11-24; просмотров: 1021; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
