Поиск циклов на ориентированном графе

Многие практические задачи сводятся к поиску циклов, то есть путей, начинающихся и заканчивающихся в одной и той же вершине. Отметим два момента. Во-первых, очевидно есть смысл искать элементарные циклы, то есть пути, не содержащие циклов внутри себя. Во-вторых, каждый цикл из K вершин порождает еще K - 1 цикл путем выбора другой начальной вершины. Например, если путь из вершин a – b – c образует цикл, то циклами будут и пути b – c - a, c – a – b. Простейший способ избежать такого повторения – нумеровать вершины графа и считать, что цикл начинает вершина с минимальным номером.

Циклы можно находить различными способами. Выберем, например, начальную вершину S и методом поиска в глубину будем искать пути S – T – R –…– S с дополнительными условиями, чтобы номера вершин T, R, … были большими, чем номер вершины S, а отличные от S вершины в пути не повторялись. Если из некоторой промежуточной вершины B не находится путь в вершину S, имеет смысл временно запретить эту вершину, чтобы не повторять бесполезных попыток. Перебирая начальные вершины, можно найти все циклы.

Поиск данных

Последовательный, индексно-последовательный, бинарный поиск

Типичной задачей многих приложений является поиск нужной информации в большом объеме данных. Для дальнейшего изложения введем ряд определений.

Таблицей будем называть совокупность однотипных элементов или записей. Запись делится на именуемые поля. Будем считать, что есть возможность прямого доступа к каждой записи таблицы.

Совокупность полей, идентифицирующая запись, называется ключом. Ключ может быть уникальным, когда его значение однозначно определяет запись, или неуникальным. В простейшем случае ключом является единственное поле записи. Ключ может быть как числовым, так и символьным.

Чаще всего встречаются следующие задачи поиска:

· найти любую запись с заданным значением ключа;

· найти первую запись с заданным значением ключа;

· найти все записи с заданным значением ключа;

· найти любую запись с заданным значением ключа;

· если поиск неудачен, вставить новую запись с заданным значением ключа;

· найти и удалить запись с заданным значением ключа.

Простейшим видом поиска является последовательный поиск. В зависимости от задачи поиск ведется от первой записи и до нахождения нужной или до конца.

Поиск несколько облегчается, если записи отсортированы по возрастанию или убыванию значений ключа, по которому производится поиск. Например, при сортировке по возрастанию можно прекращать поиск, как только значение ключа очередной записи окажется больше заданного значения. В среднем сортировка вдвое уменьшает трудоемкость последовательного поиска.

При всей своей простоте последовательный поиск крайне неэффективен. Он находит свое применение в тех случаях, когда объем данных невелик либо обработке подлежит большое число записей. Последовательный поиск может быть составной частью более сложных методов поиска.

Индексно-последовательный поиск позволяет сочетать возможности прямого и последовательного доступа к записям. Этот вид организации и поиска данных был настолько популярным, что поддерживался в некоторых языках программирования. В настоящее время индексно-последовательный поиск вытеснен более совершенными методами.

При индексно-последовательном поиске данные в исходной таблице располагаются в порядке возрастания (убывания) значений ключа. Создается индекс – дополнительная таблица, аналогичная оглавлению книги. В ней указываются ключи и соответствующие номера некоторых записей исходной таблицы. Например, может индексироваться каждая сотая запись или каждая запись с новым значением неуникального ключа.

Пусть для определенности записи исходной таблицы отсортированы по возрастанию значений ключа. Поиск начинается последовательным просмотром индекса. В нем находится максимальный ключ, не превосходящий заданный. Номер записи исходной таблицы, соответствующий этому ключу, определяет начальную позицию поиска, который продолжается последовательно до нахождения необходимой записи или до того момента, когда значение ключа текущей записи превзойдет величину ключа поиска. В последнем случае результат поиска отрицателен.

Индекс может быть многоуровневым. Например, для поиска в индексе создается еще один главный индекс, с которого и начинается поиск.

Недостатки индексно-последовательного поиска проявляются при необходимости корректировки таблицы. При добавлении новой записи приходится вставлять ее в необходимое место таблицы, сдвигая последующие записи. При этом номера записей меняются, что требует перестройки индекса. Другим методом является вытеснение новой записи в область переполнения. Это нарушает однородность описания таблицы, снижает эффективность обработки и создает алгоритмические сложности.

Бинарный поиск основан на идее известного численного метода половинного деления или дихотомии. Записи в таблице располагаются по возрастанию (убыванию) значений ключа поиска. Первоначально нижняя граница поиска соответствует первой, а верхняя - последней записи таблицы. Анализируется средняя запись таблицы. В зависимости от величины ключа можно сделать вывод о том, в какой половине таблицы нужно продолжать поиск. Тем самым пространство поиска сокращается вдвое, и процесс продолжается. Легко видеть, что максимальная трудоемкость поиска пропорциональна величине log₂ N, где N - размер таблицы.

 Бинарный поиск может быть составной частью других методов поиска. Например, индексно-последовательный метод может быть усовершенствован путем применения бинарного поиска в индексе, а затем и в исходной таблице.

Ниже приведен пример создания и использования индекса для отсортированного файла. Поиск в индексе – бинарный, а в файле - последовательный. Индексируется каждая пятая запись исходного файла.

Program Index;

{ Создание индекса для отсортированного файла и поиск }

Uses Crt;

Type

zap=record

         Name: string

         { далее могут быть другие поля }

      end;

ind=record

         Name: string;

         Nom: integer

   end;

Var

I, M, N, Low, High, Mid: integer;

Key, Namer: string;

B: boolean;

Zapr: zap;

Indr: ind;

Fzap: file of zap;

Find: file of ind;

Ish: text;

Procedure Vvod;

Begin

Reset(Ish);

Rewrite(Fzap);

While not Eof(Ish) do

   begin

     ReadLn(Ish,Namer);

     Zapr.Name:=Namer;

     Write(Fzap,Zapr)

   end;

Close(Ish);

Close(Fzap);

End;

Procedure SozdInd(var N: integer);

Begin

I:=5; M:=0; { номер записи в Fzap }

N:=0;  { номер записи в Find}

Rewrite(Find);

Reset(Fzap);

While not Eof(Fzap) do

   begin

     I:=I-1;

     Read(Fzap,Zapr);

     if I=0 then

       begin

         Indr.Name:=Zapr.Name;

         Indr.Nom:=M;

         N:=N+1;

{ счетчик числа записей в индексном файле }

         Write(Find, Indr);

         I:=5

       end;

     M:=M+1

   end;

Close(Find);

Close(Fzap)

End;

Procedure Poisk(Key: string; var M: integer);

{ Key-ключевое имя для поиска, N-число записей в индексном файле }

{ M-номер найденной записи в исходном файле, M = -1 – запись не найдена }

Begin

Reset(Fzap);

Reset(Find);

Low:=0;

High:=N-1;

While Low<=High do { бинарный поиск индекса }

   begin

     Mid:=(Low+High) div 2;

     Seek(Find, Mid);

     Read(Find, Indr);

     if Key=Indr.Name then

       begin

         Low:=Mid+1;

         High:=Mid

       end

     else if Key<Indr.Name then High:=Mid-1

          else Low:=Mid+1

   end;

M:=High;

{ здесь Low>High}

{ M - максимальный номер записи в индексе, для которой  Name<=Key }

{ если такой записи нет, то M = -1 }

if M >= 0 then

   begin

     Seek(Find, M);

     Read(Find, Indr);

     M:=Indr.Nom;

   end

else M:=0;

Seek(Fzap, M);

Read(Fzap, Zapr);

While not Eof(Fzap) and (Zapr.Name<Key) do

   begin

     Read(Fzap, Zapr);

     M:=M+1

   end;

if Zapr.Name<>Key then M:=-1; { имя не найдено }

    Close(Fzap);

Close(Find)

End;

Begin { начало основной программы }

ClrScr;

WriteLn;

Write('Введите имя исходного файла ');

Readln(Namer);

Assign(Ish,Namer);

Assign(Fzap,'a');

Assign(Find,'b');

Vvod;

SozdInd(N);

B:=True;

While B do

begin

   Write('Введите фамилию (признак конца - к) ');

   ReadLn(Namer);

   if Namer<>'к' then

     begin

       Poisk(Namer, M);

       Writeln('M=', M)

     end

   else B:=False

end;

Erase(Find);

Erase(Fzap)

End.

Бинарный поиск требует определенной аккуратности при работе с граничными значениями. Незначительные ошибки ведут к возможному зацикливанию либо неработоспособности программы.

 

Бинарные деревья поиска

 

Бинарным деревом поиска называется бинарное дерево из элементов, в котором ключ элемента в каждой вершине больше ключей всех элементов левого поддерева и меньше ключей элементов правого поддерева. Ниже приведен пример бинарного дерева поиска с числовыми значениями ключей.

 

 

Можно схему бинарного поиска в таблице, упорядоченной по возрастанию ключей, представить деревом поиска. В корне будет находиться элемент со средним индексом, элементы со средними индексами верхней и нижней половин таблицы составят значения левого и правого сыновей корня, следующий уровень вершин составят средние элементы всех четвертей таблицы и так далее.

Дерево поиска удобно для нахождения элемента с заданным ключом. Этот ключ сначала сравнивается с ключом корня. Если ключ корня больше, то переходим к левому сыну корня, иначе – к правому. Процесс продолжается в направлении от корня к листьям до нахождения элемента или получения отрицательного результата.

Деревья поиска применяют, например, в трансляторах для хранения и быстрого поиска ключевых слов или идентификаторов программы.

Наряду с поиском деревья поиска обеспечивают сортировку элементов. Действительно, обход дерева в порядке слева направо дает перечисление элементов по возрастанию ключей.

Включение нового элемента в дерево поиска выполняется следующим образом. Сначала производится поиск элемента с ключом, равным ключу нового элемента. После прихода в лист элемент войдет в новую вершину дерева, которая будет левым или правым сыном найденного листа в зависимости от значения ключа элемента.

Удаление элемента из дерева поиска предполагает такую перестройку дерева, чтобы оно не содержало указанного элемента, но оставалось деревом поиска. Возможны следующие три случая при удалении элемента из дерева поиска.

1. Удаляемый элемент находится в листе дерева. В этом случае удаляется соответствующая ссылка из отцовской вершины.

2. Удаляемый элемент находится в вершине с одним сыном. На место вершины с данным элементом помещается ее единственный сын со всеми своими потомками, то есть подтягивается все поддерево по имеющейся ветви.

3. Удаляемый элемент находится в вершине с обоими сыновьями. Сначала на место удаляемого элемента помещается один из двух элементов с соседними значениями ключа. Это может быть элемент с меньшим значением ключа из самой правой вершины левого поддерева либо с большим значением ключа из самой левой вершины правого поддерева. Для нахождения вершины с этим элементом достаточно спуститься из вершины с удаляемым элементом по левой ветви и далее идти по правым ветвям, пока это возможно, либо аналогичным образом найти этот элемент в правом поддереве. Найденная вершина имеет не более одного сына, поэтому дальнейшие действия сводятся к одному из первых двух случаев.

Например, удаление элемента с ключом 20 из дерева поиска, приведенного выше, даст следующий результат

 

 

Рассмотрим следующую задачу. С клавиатуры вводится последовательность слов. Требуется последовательно включать эти слова в дерево поиска, учитывая число вхождений каждого слова. Далее обеспечить удаление некоторых слов. При удалении уменьшать счетчик числа повторений слова и полностью удалять слово при обнулении этого счетчика. После каждой операции выдавать дерево поиска на экран, перечисляя вершины по алфавиту слов с указанием уровня вершин и счетчика повторений.

Program PoiskVkl;

{ поиск с включением на бинарном дереве }

Uses Crt;

Type

ref= ^word;

word=record

        Key: string;

        Count: integer;

        Left, Right: ref

     end;

Var

Root: ref;

Rab: string;

B: boolean;

Procedure Search(X: string; var P: ref);

Begin

if P=Nil then { слова нет - включить ! }

begin

   New(P);

   with P^ do

     begin

       Key:=X;

       Count:=1; Left:=Nil; Right:=Nil

     end

  end

else

  if X<P^.Key then Search(X, P^.Left)

  else

    if X>P^.Key then Search(X, P^.Right)

    else { нашли слово }

      P^.Count:=P^.Count+1

End;

Procedure Delete(X: string; var P: ref);

{ память освобождается, описатель var - обязателен }

Var

Q: ref;

Procedure Del(var R: ref); { сначала R=Q^.Left }

{ замещение Q^ самым правым элементом левого поддерева }

Begin

if R^.Right<>Nil then Del(R^.Right)

else

   begin { R-самая правая вершина левого поддерева }

     Q^.key:=R^.Key;

     Q^.Count:=R^.Count;

     Q:=R;

     R:=R^.Left; { подтянули левое поддерево }

     Dispose(Q)

   end

End;

Begin

if P=Nil then

WriteLn('Слова нет в дереве !')

else

if X<P^.Key then Delete(X, P^.Left)

else

  if X>P^.Key then Delete(X, P^.Right)

  else { X=P^.Key - нашли слово }

    if P^.Count>1 then P^.Count:=P^.Count-1

    else

      begin { полное удаление слова }

        Q:=P; { Q – указатель на удаляемую вершину }

        if Q^.Right=Nil then

          begin

            P:=Q^.Left; { подтянули левое поддерево }

            Dispose(Q)

            {работает по рекурсии: меняя P, меняется

             P^.Left или P^.Right у отцовской вершины } 

          end

        else if Q^.Left=Nil then

               begin

             P:=Q^.Right;

                 {подтянули правое поддерево }

                    Dispose(Q)

               end

             else Del(Q^.Left); { замена }

      end

End;

Procedure PrintTree(W: ref; L: integer);

{ W-корень, L-число точек, показывающее уровень дерева }

Var

I: integer;

Begin   

if W<>Nil then

with W^ do

   begin

     PrintTree(Left, L+1);

     For I:=1 to L do

       Write('.');

     WriteLn(Key, ' ', Count);

     PrintTree(Right, L+1)

  end

End;

Begin

ClrScr;

Rab:=' ';

Root:=Nil;

B:=True;

While B do

begin

   Write('Укажите слово для ввода (к-признак конца) ');

   Readln(Rab);

   if Rab<>'к' then

     begin

       Search(Rab, Root);

       PrintTree(Root, 0)

     end

      else B:=False

end;

B:=True;

While B do

begin

   Write('Слово для удаления (к-признак конца)? ');

   Readln(Rab);

   if Rab<>'к' then

     begin

       Delete(Rab, Root);

       PrintTree(Root, 0)

      end

   else B:=False

end;

End.

 

Балансировка деревьев поиска

 

Трудоемкость нахождения заданного элемента в дереве поиска зависит от структуры этого дерева. Например, если ни у одной вершины нет левого сына, то дерево вырождается в линейный список, и поиск сводится к последовательному перебору вершин. В связи с этим появляется необходимость в поддержке определенной сбалансированности дерева поиска.

По определению Вирта, дерево поиска является идеально сбалансированным, если для каждой его вершины количество вершин в левом и правом поддеревьях отличается не более, чем на 1.

В процессе корректировки идеальная балансировка дерева часто нарушается. Имеется более мягкое определение: дерево сбалансированно, если высота (глубина, количество уровней) левого и правого поддеревьев любой вершины отличается не более, чем на 1. Сбалансированные деревья поиска называют АВЛ-деревьями по именам авторов Адельсон-Вельского и Ландиса. В АВЛ-деревьях необходимость в операциях балансировки появляется реже, а сами эти операции достаточно просты.

Восстановление баланса в АВЛ-деревьях достигается путем преобразований, называемых поворотами. Имеются четыре типа поворотов: LL-поворот, RR-поворот, LR-поворот и RL-поворот. Первые два из них считаются одинарными, а последние два – двойными. Это связано с количеством операций, необходимых для восстановления баланса.

Мнемонические обозначения типов поворота связаны с ситуациями нарушения баланса, возникающими в некоторой вершине в результате включения новой вершины. Если оказывается, что в этой вершине высота левого поддерева больше на 2 уровня высоты правого поддерева, то первой буквой в мнемоническом обозначении поворота будет L. Если для левого сына этой вершины высота левого поддерева остается большей, то потребуется LL-поворот. Аналогично определяются обозначения других типов поворотов.

Рассмотрим следующие примеры. Пусть имеется АВЛ-дерево

 

и включается элемент с ключом 4 или 7. В результате LL-поворота получится дерево

 

или

 

Если же в исходное дерево включается элемент с ключом 12 или 17, то LR-поворот приведет к дереву

 

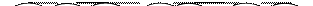
или

 

Пусть дерево описано в виде динамической структуры с указателями Left и Right на левого и правого сыновей для каждой вершины, а указатель P показывает на вершину, в которой возникло нарушение баланса. Тогда LL-поворот выражается тремя операторами

P1:=P^.Left;

P^.Left:=P1^.Right;

P1^.Right:=P;

а LR-поворот шестью операторами

P1:=P^.Left;

P2:=P1^.Right;

P1^.Right:= P2^.Left;

P2^.Left:=P1;

P^.Left:=P2^.Right;

P2^.Right:=P;

Рассмотрим примеры более сложных деревьев. Пусть имеется дерево

 

При включении элемента с ключом 1 или 3 потребуется LL-поворот в вершине с ключом 20, который в соответствии с указанными операторами приведет к дереву

 

или

 

При включении же элемента с ключом 11 или 14 потребуется LR-поворот, приводящий к дереву

 

или

 

Исключение из АВЛ-дерева несколько сложнее. Сначала исключение выполняется, как из обычного дерева поиска. Затем анализируется, есть ли нарушения баланса по направлению к корню дерева. Отличие от включения состоит в том, что балансировка может потребоваться более одного раза.

Рассмотрим в качестве примера следующее дерево.

 

Это дерево Фибоначчи: АВЛ-дерево заданной высоты с минимальным числом вершин. При удалении вершины с ключом 35 возникает нарушение баланса в вершине с ключом 30. LL-поворот приводит к новому нарушению баланса в корне дерева. В результате еще одного LL-поворота получается дерево

 

 

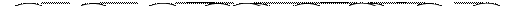
При удалении из АВЛ-дерева встречаются ситуации, когда восстановление баланса можно достигнуть как одинарным, так и двойным поворотом. Например, при удалении элемента с ключом 25 из дерева

 

 

 

баланс в корне дерева можно восстановить как LL-поворотом, так и LR-поворотом.

Б-деревья

 

До сих пор молчаливо предполагалось, что деревья поиска находятся в оперативной памяти. При увеличении их объема это становится невозможным. Конечно, можно хранить дерево и в файле с прямым доступом. В сбалансированном дереве смещение на один уровень вниз при поиске данных сокращает пространство поиска примерно вдвое, поэтому среднее число шагов поиска пропорционально величине log₂N, где N – количество вершин дерева. Если, например, N=10⁶, то эта величина близка к 20, и нерационально столько раз позиционировать файл. С другой стороны, при прямом доступе позиционирование является самой трудоемкой операцией, а чтение одного или нескольких блоков информации мало отличаются по времени. Эти соображения приводят к потребности блокирования элементов в страницы, что порождает множество вопросов.

Эту проблему удалось решить путем применения Б-деревьев - сильно ветвящихся деревьев поиска, вершинами которых являются страницы элементов.

Б-деревом порядка n называется сильно ветвящееся дерево со следующими свойствами.

1. Каждая страница , кроме корня, содержит не менее n элементов.

2. Каждая страница содержит не более 2n элементов.

3. Если страница не лист и имеет m элементов, то у нее ровно m+1 сын.

4. Если элементы нелистовой страницы с ключами A₁, A₂,…, A_m упорядочены по возрастанию ключей, то поддерево с корнем в первом сыне содержит элементы с ключами, меньшими A₁, поддерево с корнем во втором сыне - с ключами, большими A₁, но меньшими A₂ и т. д.

5. Все листовые страницы находятся на одном уровне.

Ниже приведен пример Б-дерева порядка 2. Этот порядок является тестовым, то есть иллюстрирует все принципы работы с Б-деревьями, позволяя, тем не менее, просматривать результаты вручную. В целях наглядности выбраны числовые значения ключей.

 

 

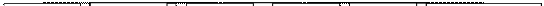
Поиск элемента с заданным ключом проводится по направлению от корня к листьям Б-дерева на основании свойства 4. Число уровней Б-дерева оценивается величиной log_nN, где N – количество элементов дерева. Для рассмотренного случая N=10⁶ эта величина равна 3, то есть по сравнению с бинарным деревом поиска для нахождения элемента требуется перебирать существенно меньшее число вершин.

Включение нового элемента в Б-дерево выполняется следующим образом. Сначала производится поиск листовой страницы, где должен располагаться новый элемент. Если в этой странице менее 2n элементов, то новый элемент добавляется в страницу без изменения структуры дерева. Если же в ней оказывается 2n+1 элемент, то средний по значению ключа элемент отправляется в отцовскую страницу, а элементы, меньшие и большие среднего элемента по значениям ключа, образуют две новые страницы по n элементов. Если в отцовской странице тоже происходит переполнение, то процесс продолжается вверх по дереву. Вытесненный элемент из корневой страницы образует новый корень, увеличивая число уровней дерева. Следовательно, Б-дерево растет снизу вверх.

Рассмотрим следующий пример. Требуется вставить элемент с ключами 7 и 75 в следующее Б-дерево.

 

 

 

Элемент с ключом 7 добавляется в крайнюю левую страницу. На крайней правой листовой странице добавление второго элемента вызовет переполнение, и элемент с ключом 68 будет вытеснен в корень. В корне тоже окажется более 4 элементов, средний из которых образует новый корень. В результате получится дерево

 

 

 

Начальная организация Б-дерева производится путем последовательного включения элементов. Для Б-дерева второго порядка второй уровень появляется после включения пятого элемента.

Исключение из Б-дерева распадается на несколько случаев. Пусть сначала исключаемый элемент находится на листовой странице дерева. Если на этой странице больше n элементов, то структура дерева не нарушается. Если же на ней ровно n элементов, то элементы этой страницы объединяется с элементами соседней страницей той же отцовской страницы и к ним добавляется элемент из отцовской страницы, ключ которого имеет промежуточное значение между ключами объединяемых страниц.

Если число объединенных элементов окажется не менее 2n+1, то средний элемент располагается в отцовской странице, а элементы, меньшие и большие среднего элемента по значениям ключей, образуют 2 страницы. 

Если число объединенных элементов будет равно 2n, то эти элементы составят единственную страницу. При этом может оказаться, что в отцовской странице станет менее n элементов. В этом случае процесс распространяется аналогично вверх по дереву. Корень дерева уничтожается, если в нем не остается элементов.

В качестве примера рассмотрим последнее Б-дерево, полученное после вставки элементов с ключами 7 и 75. При удалении элемента с ключом 36 объединяются элементы с ключами 2, 4, 7, 30, 34. Элемент с ключом 7 отправляется в отцовскую страницу вместо бывшего там элемента с ключом 30, а две измененные листовые страницы будут содержать элементы с ключами 2,4 и 30,34.

Удалим в полученном дереве элемент с ключом 75. Сейчас новую страницу образуют элементы с ключами 65,67,68,69, а в отцовской странице останется единственный элемент с ключом 60, что недопустимо. Этот элемент объединяется с элементами соседней страницы и к ним добавляется элемент с ключом 50 из корня, который остается пустым. После удаления корня дерево примет вид, имевший до вставки элементов с ключами 7 и 75. Число уровней дерева уменьшается с трех до двух.

Если удаляемый элемент находится не в листовой странице, то сначала он замещается любым из двух соседних по значению ключа элементов. Он, очевидно, находится в листовой странице. Пусть элементы каждой страницы отсортированы по возрастанию ключей, и удаляемый элемент имеет номер k в своей странице. Тогда соседними элементами являются наибольший и наименьший по значению ключей элементы поддеревьев, корнями которых являются k-й и k+1-й сын страницы с удаляемым элементом. Далее все сводится к рассмотренной выше процедуре удаления элемента из листовой страницы.

Б-деревья широко применяются для индексации данных. Индексация здесь понимается в более широком смысле как аппарат, обеспечивающий быстрый поиск данных. Почти все современные системы управления базами данных используют идексацию на основе Б-деревьев. Рассмотрим на принципиальном уровне способ индексации с помощью Б-деревьев.

Имеется исходный файл с прямым доступом к записям, которые идентифицируются значениями ключей. Записи в файле неотсортированы. Для данного файла строится Б-дерево, элементами которого являются ключи записей. Вместе с ключом сохраняется позиция соответствующей записи в исходном файле. После нахождения элемента с заданным ключом в Б-дереве определяется позиция исходного файла, где находится необходимая запись.

Б-дерево представляет собой файл прямого доступа, записями которого являются страницы. В структуре каждой страницы резервируется массивы из 2n элементов для ключей и соответствующих номеров записей исходного файла, а также массив из 2n+1 элемента для ссылок на страницы сыновей. Каждая страница в простейшем случае идентифицируется номером записи в файле, представляющем Б-дерево.

Новая запись дописывается в конец исходного файла, а ее ключ вставляется в Б-дерево с возможной перестройкой последнего. Удаление записи обычно проводят в два этапа. Удаляемая запись помечается в исходном файле без изменения Б-дерева. Доступ к помеченным записям сохраняется, поэтому любая пометка может быть снята. Физическое удаление записей производится отдельной командой. Исходный файл переписывается без помеченных записей, а Б-дерево строится с самого начала. Такой подход обеспечивает большую безопасность удаления и уменьшает трудоемкость перестройки Б-дерева за счет группировки удалений.

Хеширование

 

Вернемся к исходной задаче поиска данных. Имеется таблица элементов, характеризующихся значениями ключей. Есть возможность сравнения значений ключей, то есть на ключах задано отношение порядка. Требуется организовать поиск элемента с заданным ключом, минимизируя число обращений к таблице.

Адресом элемента таблицы будем считать его порядковый номер, считая с 0. Очень привлекательной кажется возможность определения адреса элемента по его ключу. Методы поиска, основанные на этой идее, называются адресными.

В идеальном случае существует взаимно однозначное соответствие между значениями ключей и множеством адресов таблицы. Пусть, например, элементы таблицы содержат информацию о владельцах внутренних телефонов некоторой организации. Номер телефона состоит из 3 цифр. Тогда достаточно иметь таблицу размером 1000 записей, в которой адрес элемента равен номеру телефона. Однако на практике так случается редко. Если в этом примере номера телефонов не являются внутренними и состоят из 6 цифр, то таблица должна иметь 10⁶ записей и будет почти незаполнена.

Задача состоит в построении функции, преобразующей значения ключей элементов в адреса их хранения. Такое преобразование называют хешированием, а саму функцию – хеш-функцией или функцией расстановки. Поскольку взаимно однозначное отображение малореально, неибежно возникают ситуации, когда несколько элементов с разными ключами отображаются в один адрес. Эти конфликтные ситуации называются коллизиями. Борьба с коллизиями является непременной составной частью хеширования.

Например, если в рассмотренной задаче количество имеющихся в организации телефонов меньше 1000, то адрес может соответствовать числу, образованному первыми либо последними 3 цифрами номера. Вероятно, последний вариант предпочтительнее, поскольку первые цифры определяют телефонную станцию и должны часто повторяться, но и в этом случае телефоны с одинаковами 3 последними цифрами будут вызывать коллизии.

Будем в дальнейшем считать, что значения ключа - целые неотрицательные числа. Если ключ представляет собой строку символов, можно сложить их коды либо образовать числовой ключ путем сцепления кодов первых символов, что часто используется на практике.

Построение хеш-функции представляет собой нелегкую проблему. Основными требованиями к хеш-функции являются простота вычисления и равномерность расстановки элементов по диапазону адресов. Одна и та же хеш-функция может быть удачной для одних задач и неудачной для других. Более того, для любой хеш-функции можно подобрать пример, когда она абсолютно непригодна.

Среди универсальных способов построения хеш-функции можно назвать метод середины квадрата, предложенный еще фон Нейманом для построения последовательностей псевдослучайных чисел. Метод основан на том, что при возведении в квадрат все цифры целого числа в двоичной системе счисления дают свой вклад в значения средних цифр. Если для числа выделяется N разрядов, то его квадрат имеет разрядность 2N, и значения N средних разрядов дает очередное псевдослучайное число. Зная размер таблицы, легко привести каждое полученное значение в имеющийся диапазон адресов. Мы выберем для примеров другую распространенную хеш-функцию вида H(k) = k mod N, где k-значение ключа, N-размер таблицы, H(k)-полученное значение адреса.

Пусть выполняется размещение элементов в таблице, и для очередного элемента с ключом k получен адрес h₀ = k mod N. Рассмотрим методы разрешения коллизий при хешировании.

Простейшим методом разрешения коллизий является метод линейной пробы. Если ячейка таблицы с адресом h₀ занята, то применяется функция повторного хеширования h_i = (h₀+i) mod N, где i – номер попытки размещения элемента.

Метод линейной пробы прост и обеспечивает эффективость использования памяти таблицы. Действительно, если в таблице имеется свободное место, то оно будет найдено на некотором шаге. Естественно, при поиске потребуется каждый раз сравнивать ключ очередного элемента таблицы с ключом поиска.

Недостатком метода линейной пробы является эффект скучивания. Если значительное число последовательных ячеек таблицы занята, то вероятность попадания нового элемента в первую свободную ячейку после этой группы растет пропорционально количеству элементов в группе. Такие группы ячеек разрастаются, как снежный ком, и в результате нарушается равномерность расстановки элементов, что ведет к потере эффективности поиска и включения новых элементов.

Другим способом разрешения коллизий является метод квадратичной пробы, для которого функция повторого хеширования имеет вид h_i = (h₀+i²) mod N. Этот метод не приводит к эффекту скучивания, но менее эффективен по памяти. Возможна ситуация, когда свободные ячейки в таблице имеются, но не могут быть найдены при повторном хешировании. Обычно максимально допустимое число попыток размещения элемента при использовании этого метода определяется некоторой константой или зависит от размера таблицы. Впрочем, если N-простое число, то гарантируется заполнение таблицы хотя бы наполовину. Действительно, если h_j = h_i, то j²= i² mod N или (j+i)(j-i)=0 mod N, то есть (j+i)(j-i)=cN. Считая j>i, можно сделать вывод, что j>N/2, то есть ситуация встретилась после N/2 попыток размещения элемента, во время которых места в таблице оказывались занятыми. Иными словами, ситуация возможна, когда не менее половины таблицы занята.

Еще одним способом разрешения коллизий является метод цепочек, когда элементы, распределенные начальным хешированием в одно и то же место, связываются в линейный список или цепочку. Для этого используется память помимо таблицы. При хешировании в оперативной памяти можно запросить память из кучи, во внешней памяти назначается область переполнения. Недостаток метода цепочек в том, что нарушается однородность распределяемой под элементы памяти, что ведет к усложнению алгоритмов и потере эффективности.

Для достижения высокой скорости хеширования рекомендуется резервировать память в таблице с запасом 10-50 % от ожидаемого числа элементов.

Рассмотрим простой пример хеширования с квадратичным апробированием. В качестве таблицы используется массив.

Program Heshir;

Uses Crt;

Const

P=13;   { простое число }

Raz=5; { число попыток поиска }

Type

index=0..P-1;

word=record

       Key: integer;

       Count: integer; { число включений }

       end;

Var

T: array[0..P-1] of word; { массив для расстановки }

K: integer;        { ключ поиска }

Ind, H: index;

I, Kolz: integer;  { количество записей в таблице }

B: boolean;

 Procedure Search(K:integer; var Ind: index);

{ возвращает индекс, по которому размещен элемент }

Begin

if Kolz>=P then

     begin

       WriteLn('Таблица переполнена !');

       Exit

     end;

H:=K mod P;

For I:=1 to Raz do

   begin

     WriteLn('Печать перед обработкой записи: ');

     WriteLn('H=', H, ' Count=', T[H].count);

     WriteLn('Количество записей(Kolz): ', Kolz);

     if (K=T[K].Key) or (T[K].Count=0) then

       { нашли ключ или пустое место в таблице }

      begin

         T[H].Count:=T[H].Count+1;

         if T[H].Count=1 then { запись впервые }

         Kolz:=Kolz+1;

         T[H].Key:=K;

         Ind:=H;

         Exit

       end

     else

       H:=(H+I*I) mod P

   end;

WriteLn('За ', Raz, ' попыток не нашли записи и места в   таблице !')

End;

Begin

ClrScr;

For I:=0 to P-1 do

T[I].Count:=0;

Kolz:=0;

B:=True;

While B do

begin

   Write('Введите очередной ключ (-1 - конец) ');

   ReadLn(K);

   if K<>-1 then

       begin

         Search(K, Ind);

         WriteLn

       end

     else

       B:=False

end;

End.

Как видно из примера, хеширование легко реализуется. Не требуются сложные структуры данных, не нужны какие-либо балансировки, при запасе места в таблице обеспечивается высокая скорость.

Операция удаления элементов из таблицы используется реже. Обычно в поле записи проставляют признак удаления. При включении новой записи ячейка таблицы с признаком удаления считается свободной.

Основной недостаток хеширования в том, что требуется заранее оценивать число размещаемых элементов, а это не всегда возможно. В отличие от деревьев поиска хеширование не дает сортировку элементов.

Вирт приводит следующие данные о среднем числе попыток размещения элемента в зависимости от степени заполнения таблицы, полученные теоретическим путем.

 

Степень заполнения	Число попыток
	Линейная проба	Квадратичная проба
0.1	1.06	1.05
0.25	1.17	1.15
0.5	1.50	1.39
0.75	2.50	1.85
0.9	5.50	2.56
0.95	10.50	3.15

 

Для проверки приведенных данных была разработана программа, которая дала менее оптимистические результаты. Тем не менее, в среднем достигается достаточно высокая скорость поиска и размещения элементов. Ниже приводится текст указанной программы.

Program Heshirov;

Uses Crt;

Const

M=977; { размер таблицы - простое число }

Lim=500; { предельное число попыток размещения в таблице }

Num=20; { число опытов заполнения таблицы от 0 до 95 % }

Type

field=record

        Key:word; { ключ размещаемой записи }

        Flag:boolean {TRUE - место в таблице свободно }

      end;

tsize=0..M-1;

table=array [0..M-1] of field;

result=array[ 0..100] of real;

count=array[0..100] of integer;

Var

T:table;     { заполняемая таблица }

H:tsize;     { индекс в таблице }

I, J, A: integer;

K, N: word;

R: result;     { результаты по процентам }

C: count;  { счетчики числа хеширования по процентам }

Begin

TextBackground(3);

ClrScr;

TextColor(14);

TextBackground(0);

GoToXY(35,3);

Writeln('ХЕШИРОВАНИЕ');

TextColor(11);           { цвет символов }

TextBackground(0);       { цвет фона }

GoToXY(6,4);

Write('Зависимость числа квадратичных проб от коэффициента',

   ' заполнения таблицы');

For A:=0 to 100 do

begin

R[A]:=0;

C[A]:=0

end;

For J:=1 to Num do

begin

N:=0;     { счетчик числа удачных размещений }

For H:=0 to M-1 do { очистка таблицы }

   T[h].Flag:=True;

Randomize; { случайная инициализация для Random }

Repeat

   I:=0;

   K:=Random(65000); { случайный ключ }

   H:=K mod M;   { приведение в диапазон 0 - M-1 }

   While not (T[H].Flag and

             (T[H].Key<>K) and (I<Lim)) do

     { пока не найдено свободное место   }

     { ключи без повторения, попыток не более Lim }

     begin

       Inc(I);

       H:=(K+I*I) mod M

     end;

   if T[H].Flag then { найдено свободное место }

      begin

        Inc(N);

        T[H].Key:=K;

        T[H].Flag:=False { признак заполнения }

      end;

   A:=Round(N/M*100); { процент заполнения таблицы }

   R[A]:=R[A]+I+1; {всего попыток для этого процента }

   Inc(C[A])    { число размещаемых записей }

Until A>=95    { заполнение таблицы идет до 95 % }

end;

For A:=0 to 95 do

R[a]:=R[A]/C[A]; { среднее число попыток }

TextColor(13);

TextBackground(1);

GoToXY(1,10);          { начало строки 10 }

{ выдача рамки таблицы с результатами }

Write('-');

For I:=1 to 19 do

if R[5*I]>10 then Write('----T')

else Write('---T');

Write(#8,''); { #8 - возврат назад на 1 позицию }

GoToXY(1,12);

Write('+');

For I:=1 to 19 do

if R[5*I]>10 then Write('----+')

else Write('---+');

Write(#8,'+');

GoToXY(1,11);

Write('¦');

GoToXY(1,13);

Write('¦');

{ заполнение строки процентов (от 5 до 95 с шагом 5) }

GoToXY(2,11);

For I:=1 to 19 do

if R[5*I]>10 then Write(' ',5*I:2,'%¦')

else Write(5*I:2,'%¦');

{ выдача конечных результатов }

GoToXY(2,13);

For I:=1 to 19 do

if R[5*I]>10 then Write(R[5*I]:4:1,'¦')

else Write(R[5*I]:3:1,'¦');

{ завершение прорисовки рамки }

GoToXY(1,14);

Write('L');

For I:=1 to 19 do

if R[5*I]>10 then Write('----+')

else Write('---+');

Write(#8,'-');

TextColor(10);

TextBackground(4);

GoToXY(4,23);

Write('Press any key...');

Repeat

Until KeyPressed { ожидание до нажатия клавиши }

End.

Сортировка данных

Методы внутренней сортировки

 

Сортировкой называют перестановку элементов множества в определенном порядке. Обычно целью сортировки является облегчение последующего поиска, поэтому задачи поиска и сортировки данных тесно связаны. Например, телефонный справочник может быть отсортирован по номерам телефонов, фамилиям владельцев, их адресам и т. п.

В программировании сортировка проводится обычно по возрастанию или убыванию значений ключей элементов. Рассматривают две категории сортировки: внутреннюю и внешнюю, которые называют также сортировками массивов и файлов соответственно. Основным требованием внутренней сортировки является жесткая экономия памяти, то есть сортировка производится на месте путем обмена элементов массива. Считается возможным прямой доступ к любому элементу массива по его индексу.

Критериями эффективности методов сортировки являются необходимое число сравнений ключей C и количество пересылок элементов M. Обычно операция пересылки более трудоемка, поэтому в качестве главного критерия эффективности используют величину M.

Имеются простые и усовершенствованные методы внутренней сортировки. Простые методы обеспечивают достаточную скорость для небольших массивов и входят как составная часть в усовершенствованные методы. Наиболее часто рассматривают три класса простых методов сортировки: включениями, выбором и обменом.

Рассмотрим подробнее простые методы внутренней сортировки. В качестве объекта сортировки выступает массив из n элементов A. В составе элемента есть ключ сортировки. Без ограничения общности можно считать, что элементы состоят только из ключа, поэтому их можно сравнивать между собой. Будем для определенности сортировать элементы по возрастанию значений элементов.

Сортировка простыми включениями выполняется следующим образом. Пусть первые k элементов массива A отсортированы, то есть a₁ £ a₂ £ …£ a_k. Сравним последовательно элемент a_k+1 с элементами a_k, a_k-1,… ,a₁ до выполнения соотношения a_j £ a_k+1 £ a_j+1. Элементы a_k, a_k-1,… ,a_j+1 и сдвигаются на одно место вправо, а элемент a_k+1 помещается на место элемента a_j+1. Сначала считаем, что отсортирован один элемент массива. Сортировка заканчивается, когда на “свое” место помещается элемент a_n.

Трудоемкость простого включения зависит от начального распределения элементов. Число пересылок M составляет в среднем (n²+9n-10)/4. Некоторым улучшением метода является использование бинарного поиска для включения очередного элемента в отсортированную часть массива. Это уменьшает необходимое количество сравнений, но не пересылок.

Сортировка простым выбором начинается с поиска минимального элемента массива, который обменивается затем с первым элементом. Далее находится минимальный элемент среди a₂, a₃,… ,a_n и обменивается со вторым элементом. Затем на третье место помещается наименьший элемент из a₃,… ,a_n и так далее. Обычно сортировка выбором лучше, чем включениями, однако начальная частичная сортировка не уменьшает трудоемкость метода. Число пересылок M составляет в среднем n(log ₂ n+0.6).

Метод сортировки простым обменом более известен как метод пузырька. Массив просматривается от конца к началу, больший элемент обменивается с предыдущим. После первого прохода в начале окажется минимальный элемент, затем на втором месте – второй по значению и так далее. Сортировку пузырьком можно реализовать следующим фрагментом програмы

For I:=2 to N do

For J:=N downto I do

     if A[J-1]>A[J] then

      begin 

          X:= A[J-1]; A[J-1]= A[J];

          A[j]:=X

      end;

Метод сортировки пузырьком получил свое название по аналогии с всплывающим пузырьком воздуха и, возможно, поэтому незаслуженно популярен. При каждом проходе меньшие (“легкие”) элементы поднимаются вверх. Метод ассиметричен: “легкие” элементы всплывают быстро, а “тяжелые” тонут медленно. Очевидное улучшение состоит в том, чтобы при каждом проходе запоминать, были ли обмены, и заканчивать сортировку, если их не было. Можно также запоминать место последнего обмена, чтобы выше сравнение не производить. Еще одно улучшение составляет основу шейкер-сортировки, в которой чередуются прямое и обратное направления проходов массива. Все улучшения уменьшают только число сравнений. Количество пересылок M составляет в среднем 3(n²-n)/4. Метод пузырька хуже как метода включения, так и метода выбора.

Сортировка включениями Шелла или сортировка с убывающими приращениями является усовершенствованным методом простого включения. В основе метода лежит понятие k-сортировки, при которой сортируются отдельно k частей массива A. Любая часть образуется из начального элемента и каждого k-го элемента, отсчитываемого от начального. Сортировка проводится на месте методом простого включения. Оказывается, что m-сортировка, проведенная после k-сортировки при m<k, не нарушает k-сортировки, а вносит свой вклад в конечный результат. Метод Шелла состоит в выполнении последовательности k-сортировок с уменьшающимися шагами k. Шаги сортировки h₁, h₂,…, h_t должны удовлетворять условиям h _i > h_i+1 и h_t =1. По рекомендациям Кнута,

t = [log ₃ n] – 1, h_k-1 = 3h_k+1, h_t =1 .

Количество пересылок сортировки Шелла пропорционально величине n^{1. 2}.

Сортировка выбором с помощью бинарного дерева или турнирная сортировка выполняется следующим образом. Элементы массива делятся на пары и образуют нижний уровень бинарного дерева. Минимальные элементы каждой пары составляют предпоследний уровень и в свою очередь делятся на пары и т. д. В итоге в корне дерева оказывается минимальный элемент, который выбирается для обработки. Затем он замещается в дереве величиной ¥, и процесс повторяется. Турнирная сортировка обязана своим названием схемой сравнений, напоминающей турнир с выбываниями. Метод отличается высокой скоростью, но требует больших затрат памяти для организации дерева, поэтому применяется редко.

Пирамидальная сортировка Уильямса также является усовершенствованным методом простого выбора и входит в число наиболее эффективных методов внутренней сортировки.

Пирамидой называется последовательность элементов a_k, a_k+1,…,a_r такая, что a_i £ a_2i и a_i £ a_2i+1 при i = k, k+1,…,[r/2], где [t] – целая часть числа t. В нашей задаче внутренней сортировки будем считать, что эти элементы представляют собой часть массива A с соответствующими индексами. Пирамиду удобно изображать бинарным деревом. Например, в следующей пирамиде

 

a₁

 

a₂                                                        a₃

 

a₄                  a₅                          a₆                           a₇

a₂ £ a₄ и a₂ £ a₅, а a₁  является минимальным элементом по определению пирамиды.

Если элементы a₁, a₂,…,a_r составляют пирамиду, то элементы a₂, a₃,…,a_r также являются пирамидой и могут быть изображены деревом без корня. Элементы a₃,…,a_r также являются пирамидой и т. д.

Пусть к элементам a₂, a₃,…,a_r добавляется новый элемент a₁ с неизвестным значением. Попытаемся так поменять местами элементы a₁, a₂,…,a_r, чтобы они вновь стали пирамидой. Для этого если a₁ больше a₂ или a₃, поменяем местами a₁ с минимальным из этих элементов. Если оказавшийся на новом месте элемент a₁ снова больше одного из своих сыновей, выполним аналогичный обмен. В конце концов элементы a₁, a₂,…,a_r будут пирамидой. Такая процедура называется просеиванием.

А как путем обменов организовать пирамиду из всего массива a₁, a₂,…,a_n ? Определим k=(n div 2) +1 и расположим элементы a_k, a_k+1,…,a_n в основании пирамиды. Далее будем просеивать последовательно элементы a_k-1, a_k-2,…, a₁ среди элементов с большими индексами. В результате элементы a₁, a₂,…,a_n будут представлять собой пирамиду.

Рассмотрим пример начальной организации пирамиды из массива 25, 14, 18, 11, 31, 37, 15. Сначала организуем основание пирамиды

 

 

11(4)       31(5)          37(6)      15(7)

 

где в скобках указаны индексы массива.

После просеивания элементов 18 и 14 пирамида примет вид

11(2)                               15(3)

 

14(4)        31(5)         37(6)       18(7)

 

Наконец, после просеивания первого элемента 25 получится пирамида

11(1)

 

14(2)                               15(3)

 

25(4)        31(5)         37(6)       18(7)

 

Не всегда пирамида оказывается настолько правильной, как сейчас. Например, из элементов массива 5, 11, 14, 7, 3, 8, 1, 9, 18, 6 получится пирамида

1(1)

 

3(2)                               5(3)

 

7(4)             6(5)         8(6)       14(7)

 

        9(8)     18(9) 11(10)

 

Итак, массив a₁, a₂,…,a_n представляет собой пирамиду. Поместим элемент из корня на место последнего элемента массива, а последний элемент просеем среди элементов a₁, a₂,…,a_n-1. Элемент из корня отправим на место предпоследнего элемента, а предпоследний элемент просеем среди элементов a₁, a₂,…,a_n-2. Продолжая процесс, в итоге получим отсортированный по убыванию массив A.

Ниже приводится программа пирамидальной сортировки.

 

Program Piramida; { пирамидальная сортировка }

Uses Crt;

Const M=100; { например }

Type Index=0..m;

Var

A: array [1..M] of integer;

L, R, N: index;

I, J, K, X: integer;

B: boolean;

Procedure Vvod(var n: Index);

{ N-фактическое число элементов }

Begin

B:=True; N:=0;

While B do

   begin

     Write('Введите ключ (-1 - конец): ');

     ReadLn(L);

     if L>=0 then

begin

         N:=N+1;

A[N]:=L;

       end

     else B:=False

   end;

End;

Procedure Vivod;

Begin

WriteLn;

For I:=1 to N do

   Write(' ', A[I])

End;

Procedure Proseiv;

{просеивание элемента A[K] в пирамиде A[K+1], …, A[R] }

Begin

B:=True; I:=K; J:=2*K; X:=A[K];

While (J<=R) and B do

   begin

     if J<R then { иначе один преемник у A[K] }

       if A[J]>A[J+1] then J:=J+1;

     if X>A[J] then

       begin { спуск на уровень }

         A[I]:=A[J]; I:=J; J:=2*J

       end

     else B:=False

     {в 2 последних операторах IF знаки сравнения '<' }

     {если в корень пирамиды посылается MAX значение }

   end;

   A[I]:=X;

End;

Begin { основная программа }

ClrScr;

Vvod(N);

K:=(N div 2)+1; R:=N;

While K>1 do

begin

   K:=K-1;

   Proseiv

end;

{ далее сортировка пирамиды на месте }

{ сейчас K=1 }

While R>1 do

begin

   X:=A[1]; A[1]:=A[R]; A[R]:=X; R:=R-1;

   Proseiv

end;

Vivod;

ReadLn

End.

 

Если требуется сортировка по возрастанию, то в определении пирамиды нужно изменить знаки сравнения на противоположные. Тогда в процедуре просеивания на верхних уровнях пирамиды будут находиться большие элементы. В примечаниях процедуры Proseiv указывается, что смена знаков в двух последовательных условных операторах меняет порядок сортировки на противоположный: по возрастанию значений элементов.Среднее число пересылок элементов M в методе пирамидальной сортировки составляет (n log ₂ n)/2.

Сортировка с разделением или быстрая сортировка Хоара является усовершенствованным методом простой обменной или сортировки. Если метод пузырька наименее эффективный метод внутренней сортировки, то сортировка Хоара имеет славу наиболее быстрого метода.

Пусть элементы массива A расположены по убыванию. Для изменения порядка сортировки можно первый элемент массива поменять с последним, второй с предпоследним и так далее. Этот принцип лежит в основе сортировки Хоара.

Выберем случайным образом некоторый элемент массива X=a_k. Будем перемещаться по массиву слева направо, увеличивая индекс i, до выполнения условия a_i ³ X. Затем пойдем справа налево, уменьшая индекс j, до выполнения условия a_j £ X. Если выполнится условие i £ j, поменяем местами a_i и a_j. Продолжим этот процесс, пока индексы i и j не перехлестнутся, то есть до выполнения условия i > j. В результате из массива будут выделены две части, в первой из которых значения элементов будут не больше X, а во второй не меньше X. К обеим частям массива применим ту же процедуру.

В качестве случайного элемента можно выбрать средний элемент массива. Рассмотрим описанную процедуру на примере массива 60, 63, 10, 51, 51, 51, 85, 3, 24, 55. Разделяющим элементом является пятый элемент массива, равный 51. Стрелками показаны обмениваемые элементы.

60 63 10 51 51 51 85 3 24 55

 

 

В результате получим массив 24, 3, 10, 51, 51, 51, 85, 63, 60, 55. Значение i окажется равным 6, а j примет значение 4. Далее будем по отдельности сортировать первые 4 и последние 5 элементов массива A.

Ниже приведен рекурсивный вариант программы, выполняющей сортировку Хоара.

Program QSort; { быстрая сортировка Хоара }

Uses Crt;

Const M=100;

Type index=0..m;

Var

A: array [1..M] of integer;

K, R, N: index;

I, J, L, X, W: integer;

B: boolean;

Procedure Vvod(var N: index);

{ N-фактическое число элементов }

Begin

B:=True; N:=0;

While B do

   begin

     Write('Введите ключ (-1 - конец): ');

     ReadLn(L);

     if L>=0 then

    begin

         N:=N+1;

  A[N]:=L

       end

     else B:=False

   end;

End;

Procedure Vivod;

Begin

WriteLn;

For I:=1 to N do

   Write(' ', A[I])

End;

Procedure Sort(K, R: index);

Begin

I:=K; { нижний индекс }

J:=R; { верхний индекс }

X:=A[(K+R) div 2];

Repeat

   While A[I]<X do I:=I+1;

   While A[J]>X do J:=J-1;

   if I<=J then { A[I]>=X>=A[J] }

     begin

       W:=A[I]; A[I]:=A[J]; A[J]:=W;

       I:=I+1; J:=J-1 { стало A[I-1]<=X<=A[J+1] }

     end

Until I>J;

{ A[L]<=X для L=K,K+1,...,J }

{ A[L]>=X для L=I,...,R }

if K<J then Sort(K, J);

if I<R then Sort(I, R)

End;

Begin

ClrScr;

Vvod(n);

Sort(1, N);

Vivod;

ReadLn

End.

Можно реализовать сортировку Хоара и без использования рекурсии. Пары индексов (k, r), задающих границы сортировки, поместим в стек. Разделив часть массива, определенную парой из вершины стека, заменим эту пару двумя новыми парами индексов. Сначала в стеке будет пара (1, n), затем после первого разделения содержимым стека будут пары (1, j) и (i, n) и так далее. Очевидно, в стеке не может быть более n пар. В процессе сортировки некоторые части исчерпываются, что ведет к уменьшению числа элементов стека.

Разделяющий элемент массива не обязан оставаться на своем месте. Полезно проверить, что массив 60, 63, 10, 51, 24, 55, 90 после первого разделения примет порядок 24, 51, 10, 63, 60, 55, 90. Значение i будет равно 4, а j станет равным 3. Выделенные части массива определяются границами индексов (1, 3) и (4, 7).

Сортировка Хоара примерно вдвое быстрее пирамидальной сортировки. Среднее число пересылок элементов M в этом методе составляет ln2*(nlog ₂ n)/3.

Приведем данные Вирта, показывающие сравнительную эффективность методов сорировки. Испытания проводились на массиве из 2048 элементов, фиксировалось время в секундах. Элементы массива располагались в трех порядках: по возрастанию значений, в случайном порядке и по убыванию значений. Судя по результатам, была выбрана машина с низким быстродействием, но важны не абсолютные значения затраченного времени, а соотношение приведенных значений для различных методов. Вместе с методами внутренней сортировки указаны характеристики по методу простого слияния, который является типичным представителем внешней сортировки. Для сравнения этого метода с методами внутренней сортировки данные размещались в оперативной памяти. Описание метода простого слияния будет приведено ниже.

 

Метод сортировки	По возрастанию	Случайно	По убыванию
Простое включение	0.22	50.74	103.80
Включение с бинарным поиском	1.16	37.66	76.06
Простой выбор	58.18	58.34	73.46
Пузырьковая	80.18	128.84	178.66
Шейкер-сортировка	0.16	104.44	187.36
Шелла	0.80	7.08	12.34
Пирамидальная	2.32	2.22	2.12
Быстрая Хоара с рекурсией	0.72	1.22	0.76
Быстрая Хоара без рекурсии	0.72	1.32	0.80
Простое слияние	1.98	2.06	1.98

 

Методы внешней сортировки

 

Обектом внешней сортировки является файл. Размеры файла принципиально не ограничены, то есть он может не помещаться в оперативной памяти. Для этого вида сортировки дополнительные расходы внешней памяти жестко не нормируются, поэтому активно используются вспомогательные файлы. Доступ к файлам строго последовательный. Это требование обусловлено двумя обстоятельствами. Во-первых, методы внешней сортировки должны быть работоспособными при хранении файлов на устройствах последовательного доступа типа магнитных лент. Во-вторых, при использовании прямого доступа основные затраты времени связаны с позиционированием файлов, что желательно исключить.

В основе методов внешней сортировки лежит процедура слияния, заключающаяся в объединении двух или более отсортированных последовательностей. Рассмотрим эту процедуру на примере слияния двух последовательностей A и B в последовательность C. Пусть элементы A и B отсортированы по возрастанию, то есть a₁ £ a₂ £ …£ a_m и b₁ £ b₂ £ …£ b_n . Требуется, чтобы последовательность C также располагалась по возрастанию, то есть выполнялось c₁ £ c₂ £ …£ c_m+n.

Сначала в качестве текущих выбираются первые элементы последовательностей. Меньший из них записывается в C, и вместо него текущим становится следующий элемент этой же последовательности. Эта операция повторяется до исчерпания одной из последовательностей, после чего в C дописывается остаток другой последовательности.

Можно заметить, что доступ к элементам A, B и C выполнялся строго последовательно. В методах внешней сортировки в качестве последовательностей A, B и C фигурируют отсортированные участки файлов.

Базовым методом внешней сортировки является метод простого слияния. Рассмотрим его на следующем примере. Пусть имеется файл A, включающий элементы 27, 16, 13, 11, 18, 25, 7. Этот файл разделяется на два файла B и C путем поочередной записи элементов в эти файлы. Покажем это схемой

B: 27, 13, 18, 7

A: 27, 16, 13, 11, 18, 25, 7

C: 16, 11, 25

Затем файлы B и C снова соединяются путем поочередного включения в C элементов из A и B. При этом первым располагается меньший элемент каждой пары. Получится следующий результат

B: 27, 13, 18, 7

A: 16, 27,’ 11, 13,’ 18, 25, ‘ 7

C: 16, 11, 25

Пары отделяются друг от друга апострофами. На следующем этапе снова происходит разделение файла A на B и C, но в каждый файл пишутся поочередно уже не отдельные элементы, а выделенные пары. Получаем

B: 16, 27,’ 18, 25

 A: 16, 27,’ 11, 13,’ 18, 25, ‘ 7

C: 11, 13,’ 7

Далее происходит соединение пар в упорядоченные четверки путем использования процедуры слияния

B: 16, 27,’ 18, 25

A: 11, 13, 16, 27,’ 7, 18, 25

C: 11, 13,’ 7

Затем файл A распределяется по четверкам элементов и при новом соединении будет состоять из упорядоченных восьмерок элементов. В нашем примере сортировка закончится на этом этапе. В общем случае длина отсортированных серий будет увеличиваться по степеням 2, пока величина серии не превзойдет количество элементов в файле.

На этом примере определим основные термины внешней сортировки. В методе участвовали 3 файла, поэтому он называется трехленточным. Для выполнения сортировки потребовалось 3 прохода. Отдельный проход состоял из процедур разделения и слияния, каждая из которых обрабатывала все элементы. Такие процедуры называют фазами. Следовательно, метод простого слияния является двухфазным и трехленточным.

Есть очевидное усовершенствование метода. Результат слияния сразу распределяется на две ленты, то есть в процессе участвуют уже 4 ленты. За счет дополнительной памяти число операций перезаписи уменьшается вдвое. Это однофазный четырехленточный метод, называемый также сбалансированным слиянием.

Как видно из приведенных выше данных, метод может конкурировать по скорости с самыми быстрыми методами внутренней сортировки, но не применяется в таком качестве, так как требует значительных затрат памяти. Число проходов оценивается величиной log ₂ n, а общее число пересылок M пропорцинально n log ₂ n.

Метод простого слияния не дает какого-либо выигрыша в тех случаях, когда файл A полностью либо частично отсортирован. Этот недостаток отсутствует в методе естественного слияния.

Назовем серией последовательность элементов a_i, a_i+1, …, a_j, удовлетворяющих соотношениям a_i-1 > a_i £ a_i+1 £ …£ a_j > a_j+1. В частных случаях серия может находиться в начале или конце последовательности.

Исходный файл A разбивается на серии. Распределение на B и C ведется по сериям. При соединении сливаются пары серий. Снова возможен как трехленточный, так и четырехленточный вариант метода. Ниже показан пример сортировки методом естественного слияния c 4 лентами.

 

B: 17, 25, 41, ‘6

A: 17, 25, 41, ‘ 9, 11, ‘ 6, ‘ 3, 5, 8, 44

C: 9, 11, ‘ 3, 5, 8, 44

 

A: 9, 11, 17, 25, 41         B: 3, 5, 6, 8, 9, 11, 17, 25, 41, 44

D: 3, 5, 6, 8, 44               C:

 

При последнем разделении лента C оказывается пустой, и отсортированный файл остается на ленте B.

Метод естественного слияния в целом быстрее, но требует большего числа сравнений, так как требуется определять конец каждой серии. Ниже приведена программа сортировки файла двухфазным трехленточным методом естественного слияния.

 

Program SortSlian;

{ 3-ленточная, 2-фазная сортировка естественным слиянием }

{ на текстовых файлах, ключи целые и положительные }

{ 2 параметра командной строки: <входной файл> <выходной файл>

в VP21 счет 5 сек. на 100000 записей}

Var

name: string; { имя исходного файла }

a,b,c: text; { ленты }

k,l: longint;

key,key1,key2: longint;

e: boolean;

Procedure Soob(mess: string); { аварийное сообщение с выходом }

Begin

Writeln(mess);

Readln; { пауза }

Halt { конец }

End;

Procedure CopyFile(var f1,f2:text);

Begin

Reset(f1);

Rewrite(f2);

While not eof(f1) do

   begin

     ReadLn(f1,key);

     WriteLn(f2,key);

   end;

Close(f1);

Close(f2);

End;

Procedure Pech(var f:text);

Begin

Reset(f);

While not eof(f) do

   begin

     ReadLn(f,key);

     Write(key,' ')

   end;

Writeln

End;

Procedure CopyElem(var x,y: text;

                var buf: longint; var e: boolean);

{ копирование элемента и считывание следующего }

{ в K с проверкой конца серии (E = true) }

Begin

k:=buf;

WriteLn(y,buf);

if not eof(x) then ReadLn(x,buf)

else buf:=-7; { достигнут конец файла }

e:=(buf<k) { E=TRUE в конце серии }

End;

 

Procedure CopySer(var x,y: text; var buf:longint);

{ копирование серии из X в Y }

{ в начале buf-первый элемент текущей серии на X }

{ в конце buf-первый элемент следующей или -7 (конец X) }

Begin

if buf>0 then { файл X не считан }

   Repeat

     CopyElem(x,y,buf,e)

   Until e

End;

 

Procedure Raspred;

{ распределение A ---> B и C }

Begin

Reset(a);

ReadLn(a,key); { первый элемент из A }

Rewrite(b);

Rewrite(c);

Repeat

   CopySer(a,b,key); { key-первый элемент следующей серии }

   if key>0 then { файл A скопирован не весь }

     CopySer(a,c,key)

Until key<0

End;

 

Procedure Slian;

{ слияние B и C--->A }

Var

e1,e2: boolean;

Procedure SlianSer;

{ слияние серий из B и C ---> A }

{ key1 и key2 - первые элементы серий }

{ key1<0 - весь файл B считан, key2<0 - файл C считан }

Begin

   Repeat

     e1:=false;

     e2:=false;

     if (key1>0) and ((key1<key2) or (key2<0)) then

     { файл B не считан и текущий элемент B меньше, }

     { чем в C, либо файл C полностью считан }

       begin

         CopyElem(b,a,key1,e1);

         if e1 then  { достигнут конец серии на B }

             CopySer(c,a,key2)

       end

      else

       begin

         CopyElem(c,a,key2,e2);

         if e2 then  { достигнут конец серии на C }

            CopySer(b,a,key1)

       end

   Until e1 or e2

End;

 

Begin { начало Slian }

Reset(b);

Reset(c);

if not (eof(b) or eof(c)) then

   begin     { оба файла не пусты }

     Rewrite(a);

     ReadLn(b,key1);

     ReadLn(c,key2);

     l:=0; { счетчик числа серий }

     While (key1>0) or (key2>0) do

       begin

         SlianSer;

         l:=l+1

       end

   end

End;

 

Begin { начало основной программы }

if ParamCount<>2 then

  Soob('Ошибка! Параметры командной строки: '+

       '<входной файл> <выходной файл>')

else Assign(b,ParamStr(1));

name:=ParamStr(1);

{$I-} { отключение прерывания при ошибке ввода }

Reset(b);          { b - входной файл }

{$I+}

if IoResult<>0 then Soob('Ошибка открытия файла '+name);

Assign(a,ParamStr(2)); { a - выходной файл }

CopyFile(b,a);

Assign(b,'rab1');

Assign(c,'rab2');

l:=0;  { l-число серий после слияния - параметр }

Repeat

Raspred;                 { фаза распределения }

Writeln('Файл C: '); Pech(c); }

Slian                    { фаза слияния }

Until l<=1; { L=0, если исходный файл отсортирован }

Writeln('Файл A в конце: ');

ReadLn; }

Close(a);

Close(b); Erase(b);

Close(c); Erase(c);

End.

 

Стоит обратить внимание на процедуру копирования элемента с ленты на ленту CopyElem. Реально в файл записывается элемент из оперативной памяти, оставшийся от предыдущего копирования, а в память читается следующий элемент данного файла. Это связано с необходимостью постоянной проверки конца серии. Приходится особо учитывать случай, когда конец серии совпадает с концом файла. При слиянии считается количество получившихся серий. Сортировка заканчивается, когда остается единственная серия.

Эффективность сортировки можно повысить, используя многопутевое слияние, в котором распределение выполняется на k лент. Поскольку число серий на каждом проходе уменьшается в k раз, количество пересылок M пропорционально величине n log_kn. Если общее число лент четное, то можно использовать однофазный метод слияния, распределяя серии с одной половины лент на другую. Платой за повышение эффективности многопутевого слияния являются, как всегда, увеличение сложности реализации и дополнительные затраты внешней памяти.

На сколько может отличаться количество серий после разделения? На первый взгляд кажется, что не более, чем на одну, но это не так. Например, при распределении серий 17, 25, 41, ’ 9, 60, ‘ 50, 52, ‘ 7 первая и третья серии сливаются в общую серию, что не происходит со второй и четвертой сериями. В результате при последующем слиянии серии на одной из лент могут закончиться раньше, и придется впустую переписывать остаток другой ленты, теряя эффективность. Подобные ситуации учитываются в методе многофазной сортировки. Рассмотрим его на примере трех лент.

Пусть при соединении лент B и C на ленту A серии на B заканчиваются раньше. Тогда лента B объявляется выходной, а лента A становится входной. Процесс продолжается до нового повторения ситуации, когда серии на одной из входных лент заканчиваются. Многофазная сортировка возможна и при многопутевом слиянии. Например, при использовании в сортировке k лент можно постоянно иметь одну выходную ленту. При исчерпании серий на одной из k-1 входных лент эта лента становится выходной вместо предыдущей выходной ленты.

Методы внутренней и внешней сортировок могут использоваться совместно. Пусть сортируется большой по объему файл. В оперативной памяти выделяется буфер максимально возможного размера. Файл делится на блоки, соответствующие величине буфера. Блоки читаются в буфер, сортируются одним из методов внутренней сортировки и переписываются в другой файл. Сейчас каждый блок нового файла является серией достаточно большой длины, определяемой размером буфера. Остается применить один из методов внешней сортировки, использующий данные серии.

Эвристические алгоритмы

 

Рассмотрим одну знаменитую задачу. Коммивояжер должен посетить N городов и возвратиться в исходный пункт, при этом требуется минимизировать общую протяженность путешествия. Переезжая из города i в город j, он преодолевает расстояние C_ij.

Эта задача коммивояжера может, например, ставиться, когда требуется определить маршрут лиц, занимающихся выемкой монет из таксофонов. Длиной дуги в этом случае может быть расстояние или время в пути между двумя таксофонами на маршруте. В общем случае матрица расстояний несимметрична, но часто рассматривают симметричную матрицу расстояний.

Для решения задачи проще всего организовать поиск в глубину на заданном графе, но это крайне трудоемко при большой размерности графа. Можно использовать метод ветвей и границ, возвращаясь всякий раз, когда длина текущего частного решения превосходит длину лучшего решения, найденного до сих пор. Эта проверка устраняет просмотр некоторых частей дерева решений, но на самом деле она достаточно слабая. Более того, произвольный фиксированный порядок городов является причиной того, что много времени теряется, например, на исследование путей, которые начинаются с маршрута 1 – 2, когда города 1 и 2 отделяет большое расстояние. Имеет смысл начинать исследование с пары ближайших городов. Но и это соображение не спасает полностью положения, как и некоторые другие подходы в рамках метода ветвей и границ.

Для таких трудных с вычислительной точки зрения проблем один из подходов состоит в том, чтобы ослабить требование, что алгоритм должен давать оптимальный результат, и требовать лишь, чтобы результат был разумно близким к оптимальному. Ослабление ограничений на оптимальность приводит к более эффективным приближенным алгоритмам.

Часто такие алгоритмы строятся на основе некоторых разумных предложений, которые называют эвристиками, а сами алгоритмы – эвристическими. Обычно невозможно доказать, что эвристический алгоритм всегда находит решение близкое к оптимальному. Качество эвристического алгоритма проверяется на практике.

Рассмотрим некоторые эвристические алгоритмы для решения задачи коммивояжера. Наиболее известный из них - алгоритм ближайшего соседа. В качестве начальной точки произвольно выбираем один из городов. Среди всех еще не посещавшихся городов в качестве следующего выбираем ближайший к только что выбранному. Так продолжаем, пока не придем в последний город, после чего возвращаемся в исходный город. Алгоритм ближайшего соседа можно реализовать за время, пропорциональное N².

Есть более эффективные алгоритмы, использующие идеи алгоритмов Прима и Крускала построения остовного дерева графа. Алгоритм включения ближайшего города на каждом шаге добавляет город, еще не вошедший в маршрут, но ближайший к некоторому городу, уже принадлежащему маршруту. Новый город включается после того города из маршрута, который был ближайшим к нему. Этот алгоритм сложнее предыдущего, но также может быть реализован за время O(N²). Доказано, что если матрица симметрична и удовлетворяет неравенству треугольника (C_ij = C_ji и C_ij ≤ C_ik + C_kj для любых i, j, k), то найденный путь не более, чем в 2 раза длиннее оптимального.

В “жадном” алгоритме, как и в алгоритме Крускала, сначала рассматриваются самые короткие ребра. Очередное ребро принимается в том случае, если не приводит к появлению вершины со степенью 3 и более и не образует цикл, за исключением присутствия в цикле всех вершин. Совокупности ребер, выбранных в соответствии с этими критериями, образуют множества несоединенных путей. Такое положение сохраняется до последнего шага, когда единственный путь замыкается, образуя маршрут.

Рассмотрим для примера шесть “городов” A, B, C, D, E, F, заданных координатами A(0, 0), B(4, 3), C(1, 7), D(15, 7), E(15, 4), F(18, 0). Сначала выбирается ребро DE, имеющее кратчайшую длину 3. Затем включаются ребра AB, BC, EF, имеющие длину 5. Следующим кратчайшим ребром является AC, длина которого 7.08. Однако это ребро образует цикл с ребрами AB и BC, поэтому отвергается. Следующее ребро BE повышает степени вершин B и E до 3, поэтому тоже отвергается, как и ребро BD. Затем рассматривается и принимается ребро CD. Образовался путь A, B, C, D, E, F. Завершая маршрут, выбираем ребро AF.

C                                   D

                                           

E

 B                                      

     

A                                                  F

 

В результате получен маршрут протяженности 50. Оптимальным является маршрут A, C, D, E, F, B, A, имеющий длину 48.39. Эвристический алгоритм привел к маршруту, который всего на 4 % больше оптимального.

Трудоемкость алгоритмов

В предыдущих разделах мы уже не раз сталкивались с оценкой трудоемкости алгоритмов, то есть объема необходимых расчетов. Часто эта важнейшая характеристика алгоритмов недооценивается студентами.

Рассмотрим наглядный пример. Пусть требуется найти кратчайший путь на графе из 30 вершин, в котором каждая вершина связана со всеми другими. Как известно из начальной части курса, для решения этой задачи часто используют алгоритм Дейкстры, трудоемкость которого пропорциональна N², где N – количество вершин графа. В математике для этого случая принято обозначение O(N²).

Попробуем найти кратчайший путь перебором всевозможных путей, что проще всего реализуется поиском в глубину. Ограничимся для простоты только путями, включающими все вершины графа. Поскольку в промежутке между начальной и конечной вершинами могут в различном порядке находиться 28 вершин, то таких путей 28! Эта величина превышает 10²⁹. Будем считать, что мы в состоянии находить и оценивать 10⁹ путей в секунду (реально значительно меньше). Значит, нам потребуется 10²⁰ секунд для просмотра всех путей. В сутках менее 10⁵ секунд, а в году менее 500 суток, то есть поиск займет более 2´10¹² лет. И это при том, что мы рассматривали только самые длинные по числу вершин пути! Нас не спасет даже компьютер, работающий в 1000 раз быстрее.

Трудоемкость алгоритмов связана с понятием сложности. Конечно, имеется в виду вычислительная сложность. Теоретическое определение сложности алгоритмов дано в [1]. Мы будем следовать описанию понятия сложности в [3], в большей степени ориентированного на практическое применение.

Входные данные задачи, как правило, характеризуются некоторым числовым параметром: количеством цифр в числе, количеством элементов в массиве и т. п. Этот параметр выражается натуральным числом и называется размерностью данных. Например, размерностью может являться число битов, которыми представлен экземпляр входных данных. В последовательностях размерностью обычно бывает ее длина.

Часто для задачи определяется максимально возможная размерность входных данных. В других случаях требуется определить максимальную размерность данных, при которой задача может быть решена за приемлемое время.

Время расчетов по алгоритму зависит от количества элементарных действий над скалярными величинами. Так время работы программы прямо пропорционально числу выполняемых операций. Главную роль в понятии сложности алгоритма играет не само по себе число действий, а характер его возрастания при увеличении размерности.

В общем случае сложностью алгоритма при размерности исходных данных n будем считать функцию F(n), определяющую наибольшее количество действий при решении задачи. Функция F(n) является неубывающей. Как правило, аналитическое выражение этой функции в реальных алгоритмах невозможно, да и ненужно. Практическое значение имеет порядок возрастания F(n) относительно n. Он задается с помощью другой функции, которая имеет простое аналитическое выражение и является оценкой для функции F(n).

Функция G(n) называется оценкой сверху для функции F(n), если существует положительное число C и натуральное m, для которых F(n) ≤ CG(n) при n > m. Такая связь обозначается в математике F(n) = O(G(n)) и читается как “ O большое от G(n)”.

Аналогично функция G(n) называется оценкой снизу для функции F(n), если существует положительное число C и натуральное m, для которых CG(n) ≤ F(n) при n >m. Такая связь обозначается F(n) = Ω(G(n)).

Функция G(n) называется оценкой для функции F(n) или F(n) является функцией порядка G(n), если существуют положительные числа C₁, C₂ и натуральное m, для которых C₁G(n) ≤ F(n) ≤ C₂G(n) при n > m. Такая связь обозначается буквой Θ (тэта): F(n) = Θ(G(n)).

Иногда используют такие определения.

Функция F(n) называется функцией порядка меньше G(n), если

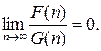
Такое соотношение обозначается буквой o (o малое): F(n) = o(G(n)).

Для оценки сложности реальных алгоритмов достаточно использования логарифмической, степенной и показательной функций, а также их сумм, произведений и подстановок. Все они монотонно возрастают и просто выражаются. Например, n (n+1) = Θ(n²). Действительно, n² < n (n+1) < 2n².

Для вычисления оценок сложности алгоритмов используют следующие два правила.

Правило суммы. Предположим, что алгоритм можно разбить на части, не имеющие общих действий. Если сложность одной части алгоритма есть Θ(G(n)), а другой Θ(H(n)), то их суммарная сложность Θ(max{G(n), H(n)}).

Правило произведения. Если часть алгоритма имеет сложность Θ(G(n)) и выполняется Θ(H(n)) раз, то общая сложность выполнения Θ(G(n) × H(n)).

Обычно оценивают наибольшую возможную сложность алгоритма и ограничиваются оценками сверху. Например, алгоритмы сортировки выбором и обменом (пузырьком) имеют одинаковую оценку сложности O(n²), где n – размерность массива. При одинаковых оценках сложности сравнивают константы или коэффициенты пропорциональности. Так пузырьковая сортировка является более медленной по сравнению с сортировкой выбором.

Как уже говорилось, величина коэффициента пропорциональности отступает на второй план в тех случаях, когда размерность данных велика. Во введении сравнивались два алгоритма с трудоемкостью 0,1´ n ² и 100´ n. При n < 1000 первый алгоритм эффективнее. Но при n = 10⁵ второй алгоритм в 100 раз быстрее первого. Подобных примеров можно привести много.

В задаче определения простоты числа n сложность алгоритма составляет O(n^1/2). Теоретически размером считают не число, а количество битов его двоичного представления (длину). Для представления числа n требуется не более m = log₂n +1 бит, т.е. размерность составляет 2^m.

Помимо точного выражения сложности используют более грубую оценку алгоритмов, подразделяя их на экспоненциальные и полиномиальные. Переборные алгоритмы имеют обычно экспоненциальную трудоемкость, то есть объем вычислений оценивается как O(aⁿ) при a > 1. Такие алгоритмы реализуемы только при ограниченных значениях n. Полиномиальные алгоритмы имеют оценку O(n ^p), где p > 0.

Оценивая сложность алгоритма определения простоты, мы первоначально в качестве размера брали само число n, а не длину log n его двоичного представления. Так была получена полиномиальная оценка O(n^1/2). В теории подобные оценки называют псевдополиномиальными, поскольку при переходе к зависимости от размера двоичного представления мы получим экспоненциальную зависимость. На практике приставку ”псевдо” обычно опускают.

Задача может иметь алгоритмы различной сложности. Неформально под сложностью задачи понимают наименьшую из сложностей алгоритмов ее решения. Сложность задач, как правило, оценить гораздо труднее, чем сложность алгоритмов. Так задача определения простоты – одна из основных в шифровании открытыми ключами. Размеры ключей измеряются тысячами битов. Для решения этой задачи применяют принципиально иные алгоритмы теории чисел, имеющие меньшую сложность. Тем не менее, сложность решения этой задачи до сих пор неизвестна.

Рассмотрим разные подходы к решению задач, которые существенно отличаются по трудоемкости.

Гомер Симпсон. Обеденный перерыв Гомера Симпсона составляет T миллисекунд. Один гамбургер Гомер съедает за N миллисекунд, один чизбургер - за M (1 ≤ M, N, T ≤ 2×10⁹). Требуется найти максимальное суммарное число гамбургеров и чизбургеров, которые Гомер может съесть в течение обеденного перерыва. Предпочтителен вариант, когда дополнительного времени остаётся как можно меньше. Выдать остаток обеденного времени.

Максимальное число гамбургеров составляет K = T div N, а чизбургеров L = T div M. Двойной цикл до K и L по трудоемкости вычислений нас устроить не может.

В [2] указан следующий простой выход. Если съедается I гамбургеров, то число чизбургеров определяется как J = (T - I × N) div M. Значит, достаточно одинарного цикла.

Но и такой подход не годится для заданной размерности. Пусть, например, M ≤ N. Очевидно, что максимальное суммарное число гамбургеров и чизбургеров составляет P = T div M. Как минимизировать остаток времени? Нужно вместо части гамбургеров съесть чизбургеры. Каждый из них потребует N - M из остатка времени. Значит, их можно съесть Q = (T - P × M) div (N - M). Тогда число гамбургеров уменьшится и составит P- Q.

Премия. Жилищная контора решила наградить своего лучшего сантехника. Был составлен список балансовых сумм по N квартирам в виде целых чисел. Числа в списке пронумеровали от 1 до N. Известно, что должники имеют отрицательный баланс. Сантехник должен выбрать часть списка, указав начальный и конечный номера. Балансы, соответствующие этому диапазону номеров, суммируются. Полученное значение составляет величину премии сантехника. Требуется определить такие начальный и конечный номера, чтобы премия оказалась максимальной.

Ввод из файла INPUT.TXT. Первая строка содержит значение N (1 ≤ N ≤ 100000). Во второй строке задаются через пробел балансы жильцов X₁,…, X_N (-1000  ≤ X_i  ≤ 1000).

Вывод в файл OUTPUT.TXT. В первой строке выводится максимальная сумма ожидаемой премии. Во второй строке выводятся начальный и конечный номера списка, соответствующие полученной сумме. Если ответов несколько, то указывается пара с минимальным начальным номером, а при одинаковых начальных номерах – пара с минимальным конечным номером.

Пример

Ввод

10

4 -19 -4 2 21 -23 15 6 -2 5 

Вывод

24

4 10

Проще всего в двойном цикле перебирать все пары с начальным и конечным номерами и для каждого интервала находить сумму чисел. Максимальная сумма даст ответ задачи. Оценим трудоемкость такого подхода. Двойной цикл в общем случае приводит к трудоемкости O(N²), а общая трудоемкость составит O(N³), что абсолютно неприемлемо.

Более рационально при первом проходе накапливать в массиве S частичные суммы, то есть определять величины S_i = X₁+ X₂+…+ X_i. Тогда X_i + X_{i +1} +…+ X_j = S_j - S_{i -1}. Такой подход обеспечивает трудоемкость O(N²), что также не может нас устроить.

Оказывается, что существует линейный алгоритм с трудоемкостью O(N), который позволяет обходиться даже без массива, обрабатывая данные за один проход напрямую из файла [7]. Будем сохранять лучшую сумму элементов R на каждом шаге и соответствующий ей интервал индексов, а также текущую сумму элементов S. Если на очередном i-ом шаге встречается положительный элемент X_i, а S<0, то начнем отсчет с начала, положив S = X_i. В противном случае прибавим значение X_i к текущей сумме S. Сравним значения R и S. Максимальную из этих величин сохраним как лучшую сумму элементов R на i-ом шаге и перейдем к следующему шагу. Ниже приводится текст программы, реализующей этот алгоритм.

 

Program BentFile; { линейный алгоритм }

Var

N,i,j,X,R,S,Res: LongInt;

{R- максимальная сумма на предыдущем шаге, S-текущая сумма} Fin,Fout: text;

Ra,Rb,Sa,Sb,a,b: LongInt;

{диапазоны индексов, обеспечивающие максимальные суммы для R,S и      общую максимальную сумму }

Begin

Assign(Fin,'input.txt');

Reset(Fin); ReadLn(Fin,N);

R:=-MaxLongInt; S:=0;

Sa:=1; Sb:=1; Ra:=1; Rb:=1; a:=1; b:=1;

For i:=1 to N do

begin

Read(Fin,X);

if (S<0) and (X>=0) then

   begin

     Sa:=i; S:=X

   end

else S:=S+X;

Sb:=i;

if X>R then

   begin

     Ra:=i; Rb:=i; R:=X

   end;

if S>R then

   begin

     Res:=S; a:=Sa; b:=Sb;

     Ra:=Sa; Rb:=Sb; R:=Res;

   end

else

   begin

     a:=Ra; b:=Rb; Res:=R;

   end;

end;

Close(Fin);

Assign(Fout,'output.txt'); Rewrite(Fout);

WriteLn(Fout,Res);

WriteLn(Fout,a,' ',b);

Close(Fout);

End.

 

Отметим в заключении, что минимальный порядок сложности – не единственный критерий выбора алгоритмов. Эффективные алгоритмы имеют, как правило, большие константы в оценке и дают реальный эффект только при большой размерности задачи. Поэтому для небольших по размерам задач менее эффективные алгоритмы могут быть быстрее.

С другой стороны, наиболее эффективные алгоритмы часто сложны и не оправдывают затрат на их реализацию. Наконец, во многих задачах важнее оказывается трудоемкость алгоритма в среднем, а не худшем случае. Например, алгоритм быстрой сортировки Хоара имеет среднюю оценку сложности O(n log n), а в наихудшем случае O(n²). Тем не менее, его используют чаще других, поскольку практически он работает всегда быстрее, чем алгоритмы с оценкой сложности наихудшего случая O(n log n).

 

9. Тестирование и отладка программ

 

Каждому программисту известно, сколько времени и сил уходит на тестирование и отладку программ. На этот этап приходится около 50% общей стоимости разработки программного обеспечения. Но не каждый из разработчиков программных средств может верно определить цель тестирования. Нередко можно услышать, что тестирование - это процесс выполнения программы с целью доказательсьва ее правильности. Но эта цель недостижима: никакое самое тщательное тестирование не дает гарантии, что программа не содержит ошибок.

Другое определение [7]: тестирование - это процесс выполнения программы с целью обнаружения в ней ошибок. Такое определение цели стимулирует поиск ошибок в программах. Отсюда также ясно, что “удачным” тестом является такой, на котором выполнение программы завершилось с ошибкой. Напротив, “неудачным можно назвать тест, не позволивший выявить ошибку в программе.

В [7, 8] сформулированы основные принципы организации тестирования:

1. Необходимой частью каждого теста должно являться описание ожидаемых результатов работы программы, чтобы можно было быстро выяснить наличие или отсутствие ошибки в ней.

2. Следует по возможности избегать окончательного тестирования программы ее автором, т.к. кроме уже указанной объективной сложности тестирования для программистов здесь присутствует и тот фактор, что обнаружение недостатков в своей деятельности противоречит человеческой психологии (однако отладка программы эффективнее всего выполняется именно автором программы).

3. По тем же соображениям организация - разработчик программного обеспечения не должна “единолично” его тестировать (должны существовать организации, специализирующиеся на тестировании программных средств).

4. Необходимо доскональное изучение результатов каждого теста, чтобы не пропустить малозаметную на поверхностный взгляд ошибку в программе.

5. Нужно тщательно подбирать тест не только для правильных (предусмотренных) входных данных, но и для неправильных (непредусмотренных).

6. При анализе результатов каждого теста необходимо проверять, не делает ли программа того, что она не должна делать.

7. Следует сохранять использованные тесты (для повышения эффективности повторного тестирования программы после ее модификации или установки у заказчика);

8. Тестирования не должно планироваться исходя из предположения, что в программе не будут обнаружены ошибки (в частности, следует выделять для тестирования достаточные временные и материальные ресурсы).

9. Следует учитывать так называемый “принцип скопления ошибок”: вероятность наличия не обнаруженных ошибок в некоторой части программы прямо пропорциональна числу ошибок, уже обнаруженных в этой части.

10. Следует всегда помнить, что тестирование - творческий процесс, а не относиться к нему как к рутинному занятию.

Существует два основных вида тестирования: функциональное и структурное.

При функциональном тестировании программа рассматривается как “черный ящик” (то есть ее текст не используется). Происходит проверка соответствия поведения программы ее внешней спецификации. Например, при функциональном тестировании программы решения квадратного уравнения наряду с нахождением корней по общей формуле нужно рассматривать случаи, когда дискриминант отрицателен, коэффициенты превращаются в нуль и т. п.

Возможно ли при этом полное тестирование программы? Очевидно, что критерием полноты тестирования в этом случае являлся бы перебор всех возможных значений входных данных, что невыполнимо.

Поскольку исчерпывающее функциональное тестирование невозможно, речь может идти о разработки методов, позволяющих подбирать тесты не “вслепую”, а с большой вероятностью обнаружения ошибок в программе. Для этого выделяют типовые случаи и ситуации. Большое количество ошибок проявляется непосредственно на границе определенного в спецификации входного или выходного условия.

При структурном тестировании программа рассматривается как “белый ящик” (т.е. ее текст открыт для пользования). Происходит проверка логики программы. Полным тестированием в этом случае будет такое, которое приведет к перебору всех возможных путей на графе передач управления программы. Даже для средних по сложности программ числом таких путей может достигать десятков тысяч. Поэтому при структурном тестировании необходимо использовать другие критерии его полноты, позволяющие достаточно просто контролировать их выполнение, но не дающие гарантии полной проверки логики программы.

Наиболее слабым из критериев полноты структурного тестирования является требование хотя бы однократного выполнения (покрытия) каждого оператора программы. Более сильным критерием является так называемый критерий С1: каждая ветвь алгоритма (каждый переход) должна быть пройдена (выполнена) хотя бы один раз.

Но даже если предположить, что удалось достичь полного структурного тестирования некоторой программы, в ней, тем не менее, могут содержаться ошибки так как:

· программа может не соответствовать своей внешней спецификации, что в частности, может привести к тому, что в ее управляющем графе окажутся пропущенными некоторые необходимые пути;

· не будут обнаружены ошибки, появление которых зависит от обрабатываемых данных (то есть на одних исходных данных программа работает правильно, а на других - с ошибкой).

Таким образом, ни структурное, ни функциональное тестирование не может быть исчерпывающим. Рассмотрим подробнее основные этапы тестирования программных комплексов.

В тестирование многомодульных программных комплексов можно выделить четыре этапа:

· тестирование отдельных модулей;

· совместное тестирование модулей;

· тестирование функций программного комплекса, то есть поиск различий между разработанной программой и ее внешней спецификацией;

· тестирование всего комплекса в целом, то есть поиск несоответствия созданного программного продукта сформулированным ранее целям проектирования, отраженным обычно в техническом задании.

На первых двух этапах используются прежде всего методы структурного тестирования, т.к. на последующих этапах тестирования эти методы использовать сложнее из-за больших размеров проверяемого программного обеспечения; последующие этапы тестирования ориентированы на обнаружение ошибок различного типа, которые не обязательно связаны с логикой программы.

Литература

 

1. Кнут Д. Искусство программирования. Тома 1-3. – М.: Издат. дом “Вильямс”, 2003.

2. Вирт Н. Алгоритмы + структуры данных = программы. – М.: Мир, 1980. – 406 c.

3. Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практика. – М.: Мир, 1980. – 476 с.

4. Трамбле Ж., Соренсон П. Введение в структуры данных. – М.: Машиностроение, 1982. - 784 с.

5. Майерс Г. Надежность программного обеспечения. – М.: Мир, 1980. – 360 с.

6. Хьюз Дж., Мичтом Дж. Структурный подход к программированию. – М.: Мир, 1980. – 278 с.

7. Фараонов В.В. Турбо Паскаль 7.0. Практика программирования: Учебное пособие. – М.: Нолидж, 1997. – 432 с.

8. Нильсон Н. Искусственный интеллект. Методы поиска решений. – М.: Мир, 1973. – 270 с.

9. Автоматизация поискового конструирования / Под ред. А.И. Половинкина. – М.: Радио и связь, 1981. – 344 с.

10. Топп У., Форд У. Структуры данных в С++. – М.: Бином, 2000. – 815 с.

11. Галочкин В.И. Структуры и организация даннных в ЭВМ: Методические указания к выполнению лабораторных и расчетно-графических работ для студентов второго курса специальности 2204. – Йошкар-Ола: 1994. – 42 с.

12. Ахо А., Хопкрофт Д., Ульман Д. Структуры данных и алгоритмы. – М.: Издат. дом “Вильямс”, 2003. – 382 с.

13. Нехорошкова Л.Г. Управление проектами: лабораторный практикум. – Йошкар-Ола: МарГТУ, 2009. – 151 с.

14. Окулов. С. М.  Программирование  в  алгоритмах. – М.: БИНОМ, 2006. –383 с.

15. Бентли Дж. Жемчужины программирования : 2-е издание. – СПб.: Питер, 2002. – 272 с.

16. Меньшиков, Ф.В. Олимпиадные задачи по программированию / Ф.В. Меньшиков. – СПб.: Питер, 2003. – 315 с.

17. Смит, Б. Методы и алгоритмы вычислений на строках. – М.: Изд. дом «Вильямс», 2006. – 496 с.

18. Галочкин В.И. Алгоритмы и программы. Задачи повышенной сложности: учебное пособие. – Йошкар-Ола: ГОУ ВПО МарГТУ, 2012. – 208 с.

Содержание

---

Дата добавления: 2018-11-24; просмотров: 805; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!