Алгоритмы поиска кратчайших путей Дейкстры и Флойда
Обычно в практических задачах длина пути измеряется не числом дуг, а их суммарной длиной. Термин длина носит обобщенный смысл. Синонимами этого термина являются расстояние, вес, стоимость дуг, причем могут рассматриваться и отрицательные значения.
Рассмотрим два алгоритма поиска кратчайших путей между вершинами: Дейкстры и Флойда. Будем считать, что длина дуги из вершины Vi в вершину Vj задана элементом матрицы aij, причем aii =0 и aij = ¥, если дуга из вершины Vi в вершину Vj отсутствует.
В алгоритме Дейкстры находится кратчайший путь из вершины S в вершину T. Вершинам присваиваются временные и окончательные метки, которые будем обозначать соответственно буквами C и D с индексами вершин.
1. Вершине S присваивается окончательная метка 0, то есть Cs :=0, временным меткам остальных вершин – значение ¥.
2. Пусть i – номер последней вершины, которой присвоена окончательная метка Ci. Каждой вершине j, имеющей временную метку Dj, присваивается новая временная метка по правилу Dj := min ( Ci + aij , Dj ). Если значение Dj меняется, то вместе с ним сохраняется номер предыдущей вершины i.
3. Наименьшая из временных меток объявляется окончательной. Пусть k – номер этой вершины. Следовательно, Ck := Dk.
4. Если новой окончательной метки не появилось, то пути из S в T нет.
5. Если вершина T не получила окончательной метки, то i := k и переход к 2.
6. Конец.
Полученная для вершины T окончательная метка дает величину кратчайшего пути. Сам путь восстанавливается от конца к началу и состоит из вершин, обеспечивших окончательные метки.
|
|
|
Пусть имеется следующий граф.
 3
3
1
 | |||
 | |||
 2
2
1
Требуется найти кратчайший путь из вершины A в вершину C.
Этапы расстановки меток удобно представить в виде таблицы. Окончательную метку будем отмечать жирным шрифтом и подчеркиванием. В скобках указывается предыдущая вершина.
| № шага | A | B | C | D | Предыдущая |
| 1 | 0 | ¥ | ¥ | ¥ | |
| 2 | 0 | 1(A) | ¥ | 2(A) | |
| 3 | 0 | 1 | ¥ | 2(A) | A |
| 4 | 0 | 1 | 4(B) | 2(A) | |
| 5 | 0 | 1 | 4(B) | 2 | A |
| 6 | 0 | 1 | 3(D) | 2 | |
| 7 | 0 | 1 | 3 | 2 | D |
Итак, длина кратчайшего пути равна 3. Окончательная метка 3 для вершины C получена из предыдущей вершины D. В свою очередь окончательная метка 2 для вершины D получена из вершины A. Следовательно, кратчайший путь составляют вершины A, D, C.
Значения окончательных меток появляются по возрастанию, то есть алгоритм Дейкстры обеспечивает поиск в ширину. Алгоритм не работоспособен при наличии отрицательных расстояний, что иллюстрирует следующий простой пример

 -3
-3
2
 1
1
Здесь кратчайший путь из A в C проходит через вершину B и равен -1, тогда как по алгоритму Дейкстры вершина C сразу получит окончательную метку 1.
|
|
|
Трудоемкость алгоритма Дейкстры пропорциональна величине N 2, где N – количество вершин графа.
Алгоритм Флойда определяет кратчайшие пути между всеми парами вершин. Снова будем считать, что длина дуги из вершины Vi в вершину Vj задана элементом матрицы aij, причем aii =0 и aij = ¥, если дуга из вершины Vi в вершину Vj отсутствует.
Пусть элемент aij ( k ) матрицы A ( k ) равен длине кратчайшего пути из вершины Vi в вершину Vj, с номерами промежуточных вершин, не превосходящими k. Тогда выполняется рекуррентное соотношение
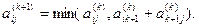 (*)
(*)
Действительно, кратчайший путь из Vi в Vj с номерами промежуточных вершин, не превосходящими k +1, может не проходить через вершину Vk +1 . В противном случае он представляет собой кратчайший путь из Vi в Vk +1, а затем из Vk +1 в Vj.
В качестве A (0) выбирается исходная матрица A. Матрица A ( n ) даст длины кратчайших путей между всеми парами вершин без каких-либо ограничений на промежуточные вершины. Значение aij ( n ) = ¥ означает отсутствие пути из вершины Vi в вершину Vj.
Параллельно с описанными матрицами строится последовательность матриц B ( i ) для нахождения самих кратчайших путей. Элемент bij ( k ) матрицы B ( k ) устанавливается равным номеру второй вершины на кратчайшем пути из Vi в Vj с номерами промежуточных вершин, не превосходящими k , и 0 в случае отсутствия путей. Элемент bij ( k +1) не меняется, если в формуле (*) минимум достигается на первом значении, и полагается равным bik +1 ( k ), если минимально второе выражение, так как в этом случае кратчайший путь проходит через вершину Vk +1.
|
|
|
Первоначально bij (0) матрицы B (0) полагается равным j, если есть дуга из Vi в Vj, и 0, если такая дуга отсутствует. Матрица B ( n ) позволяет восстановить кратчайший путь между любыми двумя вершинами. Действительно, если s = bij ( n ) дает вторую вершину на кратчайшем пути из Vi в Vj, то t = bsj ( n ) даст третью вершину, w = btj ( n ) - четвертую и так далее до попадания в вершину Vj. Значение bij ( n ) =0 означает отсутствие пути из вершины Vi в вершину Vj.
Рассмотрим в качестве примера следующий граф, в котором вершины идентифицированы номерами
 1
1
1
 2
2
5
Для него матрицы A (0) и B (0) имеют соответственно вид
| 0 | 1 | ¥ | 5 |
| ¥ | 0 | 1 | ¥ |
| ¥ | ¥ | 0 | 2 |
| 5 | ¥ | 2 | 0 |
| 1 | 2 | 0 | 4 |
| 0 | 2 | 3 | 0 |
| 0 | 0 | 3 | 4 |
| 1 | 0 | 3 | 4 |
На первом шаге допускаются пути, проходящие через вершину 1. Поскольку появляется путь 4-2-1, изменения затронут вторые элементы четвертой строки, то есть матрицы A (1) и B (1) примут вид
|
|
|
| 0 | 1 | ¥ | 5 |
| ¥ | 0 | 1 | ¥ |
| ¥ | ¥ | 0 | 2 |
| 5 | 6 | 2 | 0 |
| 1 | 2 | 0 | 4 |
| 0 | 2 | 3 | 0 |
| 0 | 0 | 3 | 4 |
| 1 | 1 | 3 | 4 |
На втором шаге допускаются пути, проходящие через вершины 1 и 2. Добавляются пути 1-2-3 и 4-1-2-3. Последний путь имеет большую длину, чем имеющаяся дуга 4-3, поэтому матрицы A (2) и B (2) примут вид
| 0 | 1 | 2 | 5 |
| ¥ | 0 | 1 | ¥ |
| ¥ | ¥ | 0 | 2 |
| 5 | 6 | 2 | 0 |
| 1 | 2 | 2 | 4 |
| 0 | 2 | 3 | 0 |
| 0 | 0 | 3 | 4 |
| 1 | 1 | 3 | 4 |
и так далее. Кратчайшие пути между всеми парами вершин будут представлены следующими матрицами A (4) и B (4)
| 0 | 1 | 2 | 4 |
| 8 | 0 | 1 | 3 |
| 7 | 8 | 0 | 2 |
| 5 | 6 | 2 | 0 |
| 1 | 2 | 2 | 2 |
| 3 | 2 | 3 | 3 |
| 4 | 4 | 3 | 4 |
| 1 | 1 | 3 | 4 |
Остовные деревья
Рассмотрим неориентированный связный граф. Остовное дерево – подграф, являющийся деревом и содержащий все его вершины. Для графа в левой части рисунка справа показаны примеры остовных деревьев




 B B B
B B B








 A C A C A C
A C A C A C
D D D
E E E
Здесь рассматриваются свободные (бескорневые) деревья, в которых корнем можно считать любую вершину.
Ряд практических задач связан с нахождением остовных деревьев. Например, множество населенных пунктов требуется связать между собой дорогами, телефонной связью, водопроводом и т. п. Если в графе заданы стоимости ребер, то встает естественная задача нахождения остовного дерева с минимальной суммарной стоимостью ребер. Наиболее распространены два алгоритма нахождения остовных деревьев: Прима и Крускала [4, 14].
Алгоритм Прима начинает построение минимального остовного дерева U с включения в него произвольной вершины u. Далее находится ребро (u, v) минимальной стоимости, связывающее множество вершин U с вершинами, не входящими в U. Вершина v и ребро (u, v) включаются в U. Процесс продолжается, пока в U не войдут все вершины графа.
Рассмотрим для примера следующий граф.



 6 5
6 5
 1
1


 5 5
5 5


 3 2
3 2
6 4

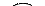
 7
7
Пусть выбрана начальная вершина 1. В остовное дерева будут последовательно добавляться вершина 3 и ребро (1, 3), вершина 6 и ребро (3, 6), вершина 4 и ребро (6, 4), вершина 2 и ребро (3, 2), вершина 5 и ребро (2, 5). Получим следующее минимальное остовное дерево
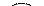

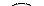
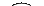
 1
1

 5
5

 3 2
3 2
4

Алгоритм Прима можно реализовать аналогично алгоритму Дейкстры. Будем в каждой вершине проставлять два типа числовых меток: временную и окончательную (постоянную).
1. Первая вершина включается в остовное дерево. Ей присваивается окончательная метка 0, остальным вершинам – временные метки ∞.
2. Всем преемникам последней вершины с окончательной меткой, имеющим временные метки, присваивается новая временная метка в виде меньшего значения ее прежней величины и стоимости ведущего в вершину ребра.
3. Минимальная из временных меток становится окончательной, а ребро вместе с новой вершиной включается в остовное дерево.
4. Переход к 2, если остаются вершины с временными метками.
После N-1 шага формирование остовного дерева заканчивается. Этапы расстановки меток по приведенному примеру представим в виде таблицы. Первые 6 колонок соответствуют вершинам. Окончательную метку будем отмечать жирным шрифтом и подчеркиванием. В скобках указывается предыдущая вершина с окончательной меткой. В последней колонке содержится общая стоимость остовного дерева в процессе формирования. Она представляет собой сумму окончательных меток.
| № | 1 | 2 | 3 | 4 | 5 | 6 | Ребро | Сумма |
| 1 | 0 | ∞ | ∞ | ∞ | ∞ | ∞ | ||
| 2 | 0 | 6(1) | 1(1) | 5(1) | ∞ | ∞ | ||
| 3 | 0 | 6(1) | 1(1) | 5(1) | ∞ | ∞ | 1-3 | 1 |
| 4 | 0 | 5(3) | 1(1) | 5(1) | 6(3) | 4(3) | ||
| 5 | 0 | 5(3) | 1(1) | 5(1) | 6(3) | 4(3) | 3-6 | 5 |
| 6 | 0 | 5(3) | 1(1) | 2(6) | 6(3) | 4(3) | ||
| 7 | 0 | 5(3) | 1(1) | 2(6) | 6(3) | 4(3) | 6-4 | 7 |
| 8 | 0 | 5(3) | 1(1) | 2(6) | 6(3) | 4(3) | ||
| 9 | 0 | 5(3) | 1(1) | 2(6) | 6(3) | 4(3) | 3-2 | 12 |
| 10 | 0 | 5(3) | 1(1) | 2(6) | 3(2) | 4(3) | ||
| 11 | 0 | 5(3) | 1(1) | 2(6) | 3(2) | 4(3) | 2-5 | 15 |
Трудоемкость алгоритма Прима составляет O(N2), где N – число вершин графа. Для разреженных графов существуют другие реализации алгоритма, основанные на более сложных структурах данных, таких как бинарная куча.
В алгоритме Краскала первоначально считается, что граф состоит из N компонент, представленных вершинами графа. На каждом шаге добавляется ребро минимальной стоимости, соединяющее две разные компоненты. Эти компоненты объединяются. В конце остается единственный компонент, который и будет являться минимальным остовным деревом.
В приведенном примере к вершинам графа будут добавляться ребра в порядке (1, 3), (4, 6), (2, 5), (3, 6), (2, 3). В результате получается то же минимальное остовное дерево, что и в алгоритме Прима.
Необходимо предусмотреть такую структуру данных, чтобы обеспечить быстрое объединение компонент. Для этого все вершины каждой компоненты должны иметь одинаковую уникальную метку. Для каждой метки можно, например, вести список всех вершин, иметющих данную метку. Тогда объединение компонент сводится к соединению двух списков.
Трудоемкость алгоритма пропорциональна M ln M при условии применения рационального алгоритма сортировки ребер по их стоимости. Если M существенно меньше N2, то есть граф разреженный, то выгоднее применение алгоритма Краскала, а не Прима.
Дата добавления: 2018-11-24; просмотров: 335; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
