Представление графа. Транзитивное замыкание
Граф представляет собой структуру, состоящую из вершин и связей между ними, называемых ребрами. Если ребра имеют направление, то они именуются дугами, а граф называется ориентированным. С помощью графов можно представить множество автомобильных дорог, связывающих населенные пункты, компьютерные сети и сети связи, электрические схемы, сетевые графики в планировании и т. п. Многие практические задачи могут быть сведены к задачам на графах.
Для представления графа чаще всего используют матрицу смежности, состоящей из нулей и единиц. Пусть имеется граф из n вершин V 1, V 2, …, Vn. Элемент aij матрицы смежности A равен 1, если имеется дуга из вершины Vi в вершину Vj, и 0 в противоположном случае. Для неориентированных графов матрица смежности симметрическая. Вместо нулей и единиц иногда задают другую информацию. Например, для дорог элемент aij может задавать расстояние между пунктами или время проезда.
Для каждой вершины Vi строка с номером i определяет возможных последователей, а i-й столбец – предшественников.
Количество путей между вершинами Vi и Vj, состоящих ровно из двух звеньев, определяется выражением
 ,
,
где суммирование ведется по всем промежуточным вершинам, для которых есть дуги из Vi и в Vj . Приведенное выражение определяет элементы матрицы A 2. Аналогично, число путей, состоящих ровно из трех звеньев, определяет матрица A 3, а число путей, не превышающих трех звеньев, можно задает матрица
|
|
|
B3= A + A2 + A3.
Можно доказать по индукции, что общее число путей между всеми парами вершин длины не более m звеньев определяется матрицей
B3= A + A2 + …+Am.
Приведенная матрица учитывает и некоторые циклические пути. Все циклические пути учесть невозможно, так как при наличии хотя бы одного цикла имеется бесконечное число разных путей, отличающихся количеством прохождения данного цикла.
Матрицей достижимости P называют матрицу из нулей и единиц, элемент pij которой равен 1, если имеется какой-либо путь из вершины Vi в вершину Vj, и 0 в противоположном случае. Если считать каждую вершину достижимой из самой себя, то ненулевые элементы матрицы Bn -1 определяют единицы матрицы достижимости. Иными словами, мы получим матрицу достижимости, если при вычислении Bn -1 считать, что единица кодирует истину, а ноль – ложь, и использовать логические операции AND и OR вместо умножения и сложения.
Матрицу достижимости называют еще транзитивным замыканием матрицы смежности. Описанный способ нахождения транзитивного замыкания отличается высокой трудоемкостью вычислений. Рассмотрим алгоритм Уоршела, дающий более эффективный способ построения транзитивного замыкания.
|
|
|
Пусть элемент pij ( k ) матрицы P ( k ) равен 1, если существует путь из вершины Vi в вершину Vj с номерами промежуточных вершин, не превосходящими k, и 0 в противоположном случае. Тогда выполняется рекуррентное соотношение
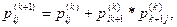
где в качестве сложения и умножения фигурируют логические операции OR и AND.
Действительно, если имеется путь из Vi в Vj с номерами промежуточных вершин, не превосходящими k, то оба элемента pij ( k ) и pij ( k +1) равны 1. Если же такого пути нет, но он появляется при добавлении вершины Vk +1 , то этот путь обязательно проходит через Vk +1 .
В качестве P (0) выбирается исходная матрица смежности. Матрица P ( n ) будет транзитивным замыканием, так как в ней не остается никаких ограничений на промежуточные вершины возможных путей.
Плюсами матрицы смежности является однородность ее структуры, возможность использования операций матричной алгебры, простой доступ к предшествующим и последующим вершинам. Недостаток заключается в нерациональных затратах памяти, так как указывается наличие или отсутствие связей между всеми парами вершин. Это особенно сказывается в разреженных графах, содержащих небольшое число связей. Матрица смежности не дает необходимой гибкости в случае постоянного изменения графа в ходе решения задачи.
|
|
|
Естественно представлять графы списком вершин и списком ребер. В этом случае для прохода по графу требуется вести трудоемкий поиск в списке ребер. Данный способ удобен в приложениях, работающих в среде систем управления базами данных.
Эффективным по памяти является использование двух связанных списков, что уже рассматривалось для деревьев. Первый из них описывает вершины графа и ссылается на ту часть второго списка, откуда начинается перечисление последователей. Такое представление неудобно при корректировках графа.
Рассмотрим один из вариантов динамического представления графов. Снова первый список соответствует вершинам. В каждой вершине имеется указатель на список дуг, исходящих из этой вершины. Дуга помимо ссылки на следующую дугу имеет указатель на ту вершину, в которую она направлена.
Пусть имеется граф
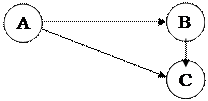 |
Приведенный способ представления приводит к следующей структуре:
 |  |  |


 Nil
Nil
 | |||
 | |||
 Nil
Nil

|
 Nil
Nil

Данная структура экономична и удобна для корректировки, хотя и несколько сложна. Предусмотрено только быстрое нахождение последователей, но не предшественников. Ведение списков предшественников еще более загромождает структуру.
|
|
|
Ниже приведен пример программы, обеспечивающей ввод и корректировку графа в описанном представлении.
Program Graph;
{ создание и распечатка графа }
Uses Crt;
Type
ukaz=^uzel;
point=^duga;
uzel=record { список вершин графа }
Nom: integer;
Next: ukaz;
Sv: point
end;
duga=record { структура дуги графа }
Next: point;
Sv: ukaz
end;
Var
A, B: integer;
L: boolean;
Top, Kon, Ua, Ub: ukaz;
P, Q: point;
Ch: char;
Begin
L:=True; Top:=Nil;
While L do
Begin
Write('Введите связи в виде пары вершин (-1 -конец) ');
Read(A);
if A=-1 then
begin
WriteLn('Ввод закончен !');
WriteLn;
L:=False
end
else
begin
Read(B);
Kon:=Top;
Ua:=Nil; Ub:=Nil;
While Kon<>Nil do
begin
if Kon^.Nom=A then Ua:=Kon;
if Kon^.Nom=B then Ub:=Kon;
if (Ua<>Nil) and (Ub<>Nil) then Kon:=Nil;
if Kon<>Nil then Kon:=Kon^.Next
end;
if Ua=Nil then { A-новая вершина }
begin
New(ua);
Ua^.Nom:=A;
Ua^.Next:=Top;
Top:=Ua;
Ua^.Sv:=Nil
end;
if Ub=Nil then { B-новая вершина }
begin
New(Ub);
Ub^.Nom:=B;
Ub^.Next:=Top;
Top:=Ub;
Ub^.Sv:=Nil
end;
if Ua^.Sv=Nil then { нет дуг у вершины A }
begin
New(p);
Ua^.Sv:=P;
P^.Next:=Nil;
P^.Sv:=Ub
end
else { есть дуги }
begin
Q:=Ua^.Sv; { первая дуга }
New(p);
P^.Next:=Q^.Next;
Q^.Next:=P;
P^.Sv:=Ub { вставка после первой дуги }
end
end
end; { конец While }
Ua:=Top;
While Ua<>Nil do
begin
WriteLn('Вершина ', Ua^.Nom);
P:=Ua^.Sv;
if P<>Nil then Write('Последователи: ')
else Write('Последователей нет !');
While P<>Nil do
begin
Kon:=P^.Sv;
B:=Kon^.Nom;
Write(B,' ');
P:=P^.Next
end;
WriteLn;
Ua:=Ua^.Next
end;
Ch:=ReadKey { пауза }
End.
Возможны и смешанные варианты представления графа. Например, для графов, допускающих существование нескольких дуг между двумя вершинами, элементами матрицы смежности могут быть указатели на соответствующие списки дуг.
Дата добавления: 2018-11-24; просмотров: 382; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
