Вычисление спектра частот собственных колебаний

 

Для вычисления спектра частот собственных колебаний достаточно рассмотреть уравнение изогнутой оси балки (15.49), подчинив его условиям закрепления ее на опорах. Из этих условий получим систему однородных уравнений, определитель которой приравниваем нулю. Это приведет к трансцендентному уравнению, собственные числа которого дадут возможность найти волновые числа k, а затем на основании (15.48) можно вычислить спектр частот собственных колебаний.

Пример 15.7.Двухопорная балка (рис. 15.13) с равномерно распределенной массой испытывает собственные колебания. Найти спектр частот собственных колебаний.

Решение. Используем уравнение изогнутой оси балки (15.49) и дважды его продифференцируем:

,

Из условий закрепления балки на левой опоре  получаем A + C =0 и A - C=0, откуда находим A + C +0. Из условий на правой опоре  получаем систему уравнений

, , .

Отсюда следует, что  и . В первом равенстве , т.к.  только при λ=0, т.е. при k=0. Но при этом и , что соответствует отсутствию перемещений. Значит B=0. Во втором равенстве , так как при D=0 не будет колебаний. Значит sin λ=0, т.е. λ=nπ, т.е. k = nπ/ l и уравнение движения сечений принимает вид:

,

а согласно (15.48) получаем спектр частот собственных колебаний

.                          (15.51)

При n=1

,   .

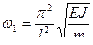Это первый тон колебаний с симметричной формой изгиба балки по одной полуволне, рис. 15.14а.

При n=2 возникает второй тон колебаний с кососимметричной формой изгиба, рис.15.14б:

, .

Бесконечное множество корней трансцендентного уравнения (15.51) определяет спектр частот с соответствующей формой колебаний. Формы колебаний зависят от способа возбуждения собственных колебаний. Можно вызвать только первую форму колебаний, если отклонить балку от положения статического равновесия прогибом посередине пролета. Можно вызвать лишь вторую форму, если отклонить балку одинаковыми перемещениями в симметрично расположенных сечениях в разные стороны от оси. Если придать балке начальный несимметричный изгиб, то возникнут все формы колебаний.

 

Метод начальных параметров в колебаниях балок

 

При наличии на балке сосредоточенных масс, а также в балках с несколькими участками, удобно применять метод начальных параметров, избегая стыковки на границах участков

Рассмотрим уравнение (15.49) и его производные:

Выразим постоянные интегрирования через начальные параметры из условий:

, , , .

Из этих условий получим зависимости:

, , , .

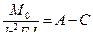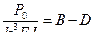Отсюда находим:

, , ,

и подставим в уравнение изогнутой оси (15.50)

. (15.52)

Здесь введены функции А.Н. Крылова:

, , ,

, , ,      (15.53)

, , ,

, , .

Уравнением (15.52) пользуются так же, как (15.50).

 

Учет сосредоточенных масс в колебаниях весомых балок

 

Если на инерционной (весомой) балке есть сосредоточенная масса M_a (рис. 15.15), то от линейных перемещений  возникает сила инерции

 

 

,

где амплитудное значение силы инерции:

                                                         (15. 54)

Амплитудное значение силы инерции P_a в уравнении изогнутой оси балки (15.52) учитывается справа от места приложения массы слагаемым, аналогичным слагаемому, содержащему P ₀, но функция  должна учитывать плечо силы инерции (z - a).

Последовательность вычисления спектра частот собственных колебаний в этом случае остается прежней – нужно рассмотреть граничные условия; получить систему однородных уравнений; определитель системы приравнять нулю, что приведет к частотному уравнению; найти корни этого трансцендентного уравнения (собственные числа), а затем согласно (15.48) вычислить частоты

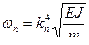.                                         (15.55)

Пример 15.8.Найти спектр частот собственных колебаний весомой консоли с погонной массой m и сосредоточенной массой М, рис. 15.16.

Решение. Согласно (15.54) учтем силу инерции в начале координат

.

Уравнение (15.52) для произвольной гармоники примет следующий вид

,

где обозначено , .

Дифференцированием находим уравнение углов поворота

.

Из условия защемления  получаем систему уравнений

,

.

Определитель этой системы приравниваем нулю

.                        (15.56)

С использованием функций Крылова (15.53) это уравнение можно привести к виду

.                           (15.57)

Если ξ=1, то из (15.57) найдем собственные числа и собственные частоты: λ₁=1,2479, λ₂=4,0311, λ₃=7,1341.

, , .

При ξ=0 трансцендентное уравнение (15.57) принимает вид

.                                                             (15.58)

Его корни:  λ₁ = 1,875, λ₂=4,694, λ₃=7,856.

Рассмотрим влияние сосредоточенной массы М на спектр частот собственных колебаний

.     (15.59)

Здесь  – частота собственных колебаний невесомой консоли с сосредоточенной массой М (см. (15.9)).

Теперь легко определить, какой сосредоточенной массой M_n следует заменить распределенную массу консоли, чтобы частота колебаний невесомой консоли была равна частоте первого тона колебаний весомой балки. Из (15.58) найден первый корень λ₁=1,8751 и точное значение частоты первого тона колебаний . Для невесомой консоли с сосредоточенной на конце балки условной массой M_n согласно (15.9) частота колебаний равна . Приравнивая эти частоты, получим коэффициент приведения массы . Такую массу нужно добавлять к сосредоточенной массе весомой балки и решать задачу о колебаниях невесомой балки с одной условной приведенной массой.

Допустим консоль с распределенной массой интенсивностью m имеет на конце балки сосредоточенную массу M = ml. Выше было получено точное значение частоты первого тона колебаний при ξ=1

.

В приближенном решении эту балку можно считать невесомой с сосредоточенной массой M=1,24267ml, а ее частота окажется равной

,

что на 0,23% меньше точного значения.

 

---

Дата добавления: 2018-11-24; просмотров: 879; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!