Собственные затухающие колебания

⇐ ПредыдущаяСтр 22 из 26Следующая ⇒

В зависимости от формы и размеров колеблющейся массы, от скорости движения и физических свойств окружающей среды может возникать линейное или квадратичное сопротивление движению. Критерием установления качества сопротивления является число Рейнольдса

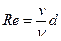, (15.14)

где v – скорость движения, d –габаритный размер движущегося объекта, 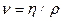- коэффициент кинематической вязкости окружающей среды (η - коэффициент внутреннего трения, ρ- плотность окружающей среды).

При 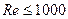возникает линейное сопротивление движению, а при 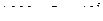проявляется квадратичный закон сопротивления с коэффициентом скоростного напора 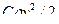(С – постоянный коэффициент лобового сопротивления, зависящий от формы движущегося объекта).

В случае сопротивления, пропорционального квадрату скорости, можно использовать квазилинейный коэффициент сопротивления k^*, который находится энергетическим методом, когда работу силы квадратичного сопротивления kv² и квазилинейного k^*v приравнивают за период колебаний в установившемся режиме движения 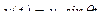. Из этих условий можно найти

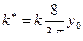. (15.15)

В связи с этим рассмотрим дифференциальное уравнение движения массы М с линейным сопротивлением движению (15.1)

, т.е.

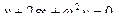. (15.16)

Здесь: 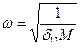- частота собственных незатухающих колебаний, 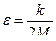- коэффициент затухания колебаний.

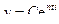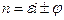Решение дифференциального уравнения (15.16) ищем в виде , что приводит к характеристическому уравнению , корни которого , где

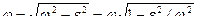(15.17)

частота собственных затухающих колебаний.

Так находим уравнение движения массы

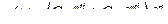или

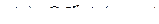. (15.18)

Здесь 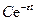- амплитуда собственных затухающих колебаний.

Дифференцируя (15.17), получим скорость движения

Из начальных условий , получаем систему уравнений

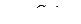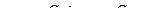позволяющую найти начальную амплитуду С и начальную фазу μ:

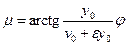, (15.19)

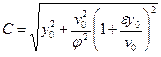. (15.20)

Так как в инженерных конструкциях чаще всего ε<<ω, то согласно (15.16) φ≈ω, т.е. частота собственных затухающих колебаний практически такая же, как частота собственных незатухающих колебаний. По этой же причине из (15.18), (15.19) получаем (15.12). Из этого следует, что изучение колебаний без учета сопротивления движению является более предпочтительным.

Вынужденные колебания без учета сопротивления движению

На невесомую упругую систему (балку) действует возмущающая нагрузка , см. рис. 15.1. Уравнение перемещения груза (15.1) принимает вид

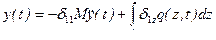Отсюда получаем дифференциальное уравнение движения массы

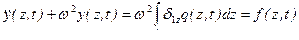. (15.21)

Решение однородного уравнения (полученного из (15.21) при 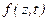) получено в (15.2).

Частное решение w(t) ищем в форме собственных функций, т.е. в виде аналогичном (15.3)

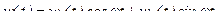. (15.22)

Дифференцируем (15.21)

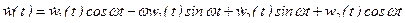
и положим

. (15.23)

С учетом (15.23) дифференцируем (15.22) вторично

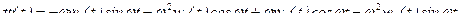
и подставляем 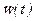и 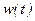в (15.20)

+ .

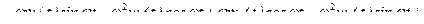
Отсюда получаем зависимость

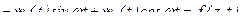. (15.24)

Решая систему уравнений (15.22) и (15.23), получаем:

, .

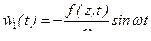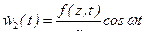Отсюда, интегрируя по временной переменной τ, получаем:

, .

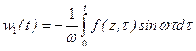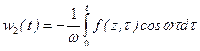Теперь в соответствии с (15.21) находим частное решение неоднородного дифференциального уравнения (15.20)

= .

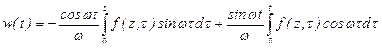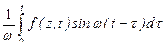Следовательно, с учетом обозначения 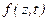в (15.20) находим частное решение на любой вид возмущающей нагрузки

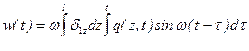. (15.25)

В случае нагрузки, не изменяющейся во времени, т.е. 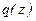, из (15.25) получаем

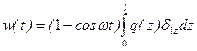. (15.26)

Но так как δ₁_z есть перемещение точки приложения массы М, от единичной силы, то интеграл 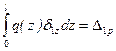представляет перемещение массы М от статического воздействия заданной нагрузки 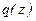. Таким образом, уравнение движения груза представляет гармоническую функцию с амплитудой в виде квазистатического прогиба в точке приложения массы

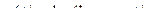. (15.27)

С учетом статического загружения балки грузом Q с перемещением 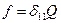получаем полное перемещение

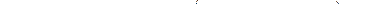. (15.28)

Здесь k _д – динамический коэффициент перемещения.

В случае сосредоточенной силы Р, когда 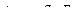динамический коэффициент

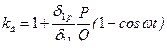. (15.29)

Пример 15.5.К невесомой консоли с сосредоточенной массой М внезапно прикладывается сила P, рис. 15.8. Найти расчетный изгибающий момент.

Решение. Согласно (15.27) динамическое перемещение массы М .

Единичное перемещение δ₁_p можно найти по методу начальных параметров

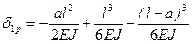Сила инерции колеблющейся массы .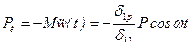

Суммарный изгибающий момент от груза Q, приложенной силы Р и силы инерции P _и

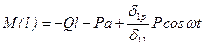В частном случае, когда a = l, динамическая нагрузка

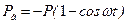. (15.30)

Ударные нагрузки

При ударном приложении нагрузки также возникают колебания. Поэтому расчетные формулы при ударе можно получить на основании вышеизложенных задач на колебания.

Рассмотрим удар неупругой массы М, падающей с некоторой высоты h на упругую невесомую систему с одной сосредоточенной массой М₀. В качестве упругой системы может быть балка, вал или стержень, испытывающие изгиб, кручение или растяжение-сжатие соответственно.

На рис. 15.8 показана невесомая балка с сосредоточенной массой М₀, на которую падает неупругая масса М со скоростью 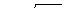. В начале совместного движения масс из закона сохранении количества движения находим начальную скорость движения 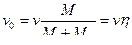(η – коэффициент передачи энергии).

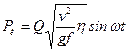От внезапного сообщения системе начальной скорости движения v ₀ возникают собственные колебания с перемещениями , и силой инерции (см. (15.13)), где f=δ₁₁Q - квазистатический прогиб в месте приложения массы от груза .

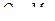Но в отличие от задачи 3 в п. 15.2 здесь нужно добавить воздействие внезапного приложения груза 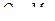, вызывающее вынужденные колебания

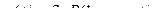с силой инерции 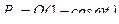, см. (15.30).

Суммарная динамическая нагрузка от удара массы М

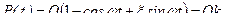здесь обозначено .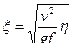

Для вычисления наибольшего значения динамического коэффициента k _д положим , т.е. 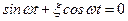, откуда находим:

, , .

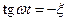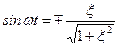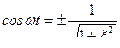Большее значение динамического коэффициента будет при верхних знаках тригонометрических функций

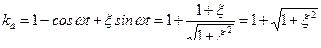С учетом обозначения ξ получаем динамический коэффициент при ударе, на который нужно умножать падающий груз Q, чтобы найти его динамическое воздействие

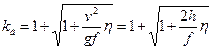. (15.31)

Итак, балку нужно рассчитывать на статическое загружение грузом и динамическое воздействие Qk _д, т.е. расчетный изгибающий момент в заделке .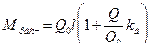

Из (15.31) следует, что минимальный динамический коэффициент k _д=2 будет при внезапном приложении нагрузки, когда h=0.

Уменьшить динамический коэффициент (15.31) можно за счет увеличения квазистатического перемещения f и уменьшения коэффициента передачи энергии η. Для этого нужно уменьшать жесткость системы и увеличивать массу, по которой производится удар.

Например, на невесомую балку (без массы М₀) с высоты 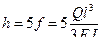падает масса М. Динамический коэффициент (15.31) при этом будет равен 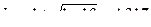. Если на балке есть масса (допустим), то коэффициент передачи энергии 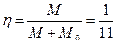и динамический коэффициент окажется равным 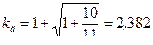. А если при этом груз падает на пружину (установленную на массе М₀) с коэффициентом жесткости 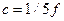, то динамический коэффициент будет практически минимальным 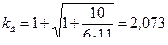(здесь квазистатическое перемещение груза равно ).

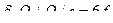Обратим внимание на то, что падающая масса М при ударе обладает энергией 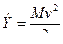, а потенциальная энергия деформации упругой системы

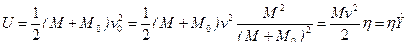Так как коэффициент передачи энергии 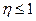, то часть энергии ударяющей массы теряется на взаимодействие между массами М и М₀. Эта потерянная энергия равна 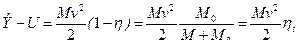. В вышеприведенном примере коэффициент потери энергии 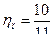и лишь 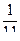энергии падающего груза идет на деформацию упругой системы.

Таким образом, если требуется передать энергию на поковку изделия, забивку гвоздя в свободно опирающуюся доску и пр., то под изделие на упругую систему нужно пристраивать по возможности большую массу. Это наковальня у кузнеца, колода у мясника, обух топора у плотника, прибивающего доски к прожилинам забора.

Дата добавления: 2018-11-24; просмотров: 234; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 17 18 19 20 212223 24 25 26 Следующая ⇒

Мы поможем в написании ваших работ!