Четвертая теория прочности (энергетическая теория формоизменения).

⇐ ПредыдущаяСтр 14 из 19Следующая ⇒

В качестве критерия прочности принимается количество удельной потенциальной энергии формоизменения, накопленной деформированным элементом.

Согласно этой теории, выдвинутой Губером (1904), опасное состояние (текучесть) в общем случае напряженного состояния наступает тогда, когда удельная потенциальная энергия формоизменения достигает своего предельного значения. Последнее можно легко определить при простом растяжении в момент текучести.

Условие наступления текучести:

U_ф = (U_ф)_т.

Условие прочности:

U_ф £ [U_ф]. (90)

Удельная потенциальная энергия формоизменения при сложном напряженном состоянии равна:

U_ф = 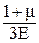[s₁²+s₂²+s₃²-(s₁s₂+s₃s₂+s₁s₃)].

При простом растяжении в момент наступления текучести (s₁=s_т; s₂=s₃=0):

(U_ф)_т = 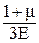s_т².

Следовательно, условие наступления текучести через напряжения можно записать в виде:

s_т.

Условие прочности будет иметь вид:

[s]= . (91)

Опыты хорошо подтверждают четвертую теорию для пластичных материалов, одинаково работающих на растяжение и сжатие.

Теория прочности предельных напряженных состояний (теория Мора).

Теория прочности предельных напряженных состояний, предложенная Мором (начало ХХ в.), основывается на предположении, что прочность материалов в общем случае напряженного состояния зависит главным образом от величины и знака наибольшего s₁ и наименьшего s₃ из главных напряжений. Среднее по величине главное напряжение лишь незначительно влияет на прочность.

Если при данных значениях s₁и s₃ нарушается прочность материала, то круг, построенный на этих напряжениях, называется предельным. Меняя предельное напряженное состояние, получим для данного материала семейство предельных окружностей (рис. 39):

Рис. 39

Опыты показывают, что по мере перехода из области растяжения в область сжатия прочность увеличивается. Это соответствует увеличению диаметров предельных окружностей по мере движения влево. Огибающая АВСД семейства предельных кругов ограничивает область прочности.

При наличии предельной огибающей расчет прочности производится весьма просто. По найденным значениям главных напряжений s₁и s₃ строим круг. Прочность будет обеспечена, если он целиком лежит внутри огибающей. Огибающую определяют путем построения по опытным данным нескольких кругов при различных комбинациях главных напряжений.

О применимости той или иной теории прочности для практических расчетов можно сказать следующее. Разрушение материалов происходит путем отрыва за счет растягивающих напряжений и путем среза за счет наибольших касательных напряжений. При этом разрушение путем отрыва может происходить при весьма малых остаточных деформациях или вовсе без них (хрупкое разрушение). Разрушение путем среза имеет место лишь после некоторой остаточной деформации (вязкое разрушение). Отсюда ясно, что первую и вторую теории прочности, отражающие разрушение путем отрыва, следует применять для материалов, находящихся в хрупком состоянии. Третью и четвертую теории прочности, отражающие наступление текучести и разрушение путем среза, следует применять для материалов, находящихся в пластическом состоянии. Теория прочности Мора является универсальной и пригодной для всех материалов.

Так как первая и вторая теории прочности имеют существенные недостатки, то в настоящее время все более утверждается мнение о нежелательности их применения.

Таким образом, для практических расчетов следует рекомендовать:

а) третью теорию (или четвертую) – для материалов, одинаково сопротивляющихся растяжению и сжатию;

б) теорию Мора – для материалов, различно сопротивляющихся растяжению и сжатию.

Следует подчеркнуть, что хрупкое или пластическое состояние материала определяется не только его характером, но и видом напряженного состояния, температурой и скоростью нагружения. Как показывают опыты, пластичные материалы при определенных условиях нагружения и температуре ведут себя как хрупкие, в то же время хрупкие материалы при определенных напряженных состояниях ведут себя как пластичные.

Так, например, при напряженных состояниях, когда все три главных напряжения – растягивающие и близки по величине, пластичные материалы ведут себя как хрупкие.

При напряженных состояниях, близких к всестороннему сжатию, хрупкие материалы могут вести себя как пластичные. При всестороннем сжатии материалы могут выдерживать, не разрушаясь, очень большие давления.

Растяжение (сжатие) стержней

Пусть стержень нагружен произвольной продольной нагрузкой. Вырежем на некотором расстоянии z бесконечно малый элемент dz (рис. 40). На данный элемент действует внешняя нагрузка и внутренние продольные силы в сечениях, по которым вырезан элемент.

Рис. 40

Составим уравнение равновесия вырезанного элемента.

- N + q_z×dz + N + dN = 0,

N’ + q_z = 0. (92)

Решение данного дифференциального уравнения с правой частью состоит из двух частей общего и частного решения и имеет вид

N(z) = C - (93)

Определим физический смысл постоянной интегрирования. При z=0:

N(0) = C.

Значение интеграла зависит от внешней приложенной нагрузки. Рассмотрим значения интеграла нагрузочных функций для наиболее часто встречающихся нагрузок.

а) сосредоточенная сила (рис. 41):

Рис. 41

при z£a Ф_N(z)=0

при z³a Ф_N(z)=-P

б) распределенная нагрузка (рис. 42):

Рис. 42

при z£c Ф_N(z)=0

при z³c Ф_N(z)=-q(z-c)

Пример

Для заданной схемы нагружения стержня (рис. 43) построить эпюру продольной силы N(z) при следующих исходных данных: q=10 кН/м, l=1м.

Рис. 43

Решение

1. Совместим начало системы координат с левым концом стержня и направим координатную ось z вдоль его продольной оси.

В соответствии со схемой нагружения разделим стержень на три участка и запишем уравнение продольных сил следующим образом:

N (z) = N (0) - 2q·z│₁+2q (z - l) │₂+ q (z - 2l) │_3.

В этом уравнении приняты следующие обозначения:

N(0) – значение продольной силы в начале координат (реакция опоры),

z – координата сечения, в котором определяется значение продольной силы.

Для решения задачи необходимо определить одну неизвестную величину – N(0). Для этого запишем граничное условие: N (3l) = 0.

Напомним, что граничные условия – это известные значения интегральных характеристик в какой-либо точке стержня.

Для определения неизвестной реакции N(0) необходимо приравнять уравнение продольных сил к нулю, подставив в нем вместо координаты «z» координату «3l»:

N (0)-2q (3l) + 2q (3l – l) + q (3l – 2l)= 0.

Решая это уравнение, найдем: N (0) = 10 кН.

2. Построение графика продольных сил.

При построении графиков уравнение рассматривается на каждом участке в отдельности и вместо координаты «z» подставляется соответствующая координата начала и конца рассматриваемого участка.

1 участок - 0 ≤ z ≤ l:

N (0) =10 кН,

N (l) = 10 – 2·10·1 = -10 кН.

2 участок - l ≤ z ≤ 2l:

N (l) = 10 – 2·10·1 + 2·10(l – l) = -10 кН,

N (2l) = 10 – 2·10·2 + 2·10(2 – 1) = -10 кН.

3 участок - 2l ≤ z ≤ 3l:

N (2l) = 10 – 2·10·2 + 2·10(2 – 1) + 10(2 – 2) = -10 кН,

N (3l) = 10 – 2·10·3 + 2·10(3 – 1) + 10(3 – 2) = 0 кН.

По рассчитанным значениям строится график продольной силы (см. рис. 43).

Кручение стержней

Пусть стержень нагружен произвольной крутящей нагрузкой. Вырежем на некотором расстоянии z бесконечно малый элемент dz (рис. 44). На данный элемент действует внешняя нагрузка и внутренние крутящие моменты в сечениях, по которым вырезан элемент.

Составим уравнение равновесия вырезанного элемента.

- М_к + m_z×dz + М_к + dМ_к = 0,

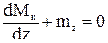М_к’ + m_z = 0. (94)

Рис.44

M_к(z) = C - . (95)

Определим физический смысл постоянной интегрирования. При z=0

М_к(0) = C.

Значение интеграла зависит от внешней приложенной нагрузки. Рассмотрим значения нагрузочных функций для наиболее часто встречающихся нагрузок.

а) сосредоточенный момент (рис. 44):

Рис.44

при z£a Ф_м(z)=0

при z³a Ф_м(z)=-L

б) распределенная нагрузка (рис. 45):

Рис. 45

при z£c Ф_м(z)=0

при z³c Ф_м(z)=-m(z-c)

Пример

Для приведённой схемы нагружения прямого стержня (рис. 46) построить эпюру крутящего момента при следующих исходных данных:

m_z = 10 кН/м, L = 10 кНм, l = 1 м.

Решение

В соответствии со схемой нагружения запишем уравнение крутящего момента в следующем виде:

M_k (z) = M_k (0) │₁ - L│₂ - m_z(z-2l) │₃.

Исходя из условий закрепления стержня, запишем следующее граничное условие: M_k (0) = 0 (реакция незакреплённого конца стержня равна нулю).

Рис. 46

Таким образом, записанное уравнение не содержит неизвестных величин и можно приступать к построению графика. Построение графика будем производить аналогично построению графика в примере 1.

1 участок - 0 ≤ z ≤ l:

M_k (0) = 0 кНм,

M_k (l) = 0 кНм.

2 участок - l ≤ z ≤ 2l:

M_k (l) = 0 – 10 = -10 кНм,

M_k (2l) = 0 – 10 = -10 кНм.

3 участок - 2l ≤ z ≤ 3l:

M_k (2l) = 0 – 10 – 10(2 – 2) = - 10 кНм,

M_k (3l) = 0 – 10 – 10(3 – 2) = -20 кНм.

По рассчитанным значениям строится график крутящего момента (см. рис. 46).

Изгиб стержней

Пусть стержень нагружен произвольной поперечной нагрузкой. Вырежем на некотором расстоянии z бесконечно малый элемент dz (рис. 47). На данный элемент действует внешняя нагрузка и внутренние поперечные силы и изгибающие моменты в сечениях, по которым вырезан элемент.

Рис. 47

Составим уравнения равновесия вырезанного элемента.

Уравнение равновесия всех сил на вертикальную ось.

- Q_y + q_y×dz + Q_y + dQ_y = 0,

Q_y' + q_y = 0. (96)

Уравнение равновесия моментов относительно центра тяжести правого сечения вырезанного элемента.

- М_х + q_y×dz×dz/2 + М_х + dМ_х - Q_y×dz = 0,

Слагаемое, выражающее момент от распределенной нагрузки – слагаемое второго порядка малости, поэтому им можно пренебречь

М_х' = Q_y. (97)

Объединяя дифференциальные уравнения (96) и (97), получим:

М_х'' = - q_y (98)

М_х(z) = C₁+С₂z – Ф_м,

где Ф_м – частное решение, отражающее внешнюю приложенную нагрузку.

Определим физический смысл постоянных интегрирования. При z=0

М_х(0) = C₁,

М_х' (0) = Q_y(0) = С₂.

Рассмотрим подробнее частное решение. Пусть стержень нагружен произвольной распределенной нагрузкой (рис. 48). Определим величину поперечной силы и изгибающего момента для точки с координатой z.

Рис. 48

Q_y = ,

М_х = . (99)

Значения интегралов зависят от внешней приложенной нагрузки. Рассмотрим значения нагрузочных функций для наиболее часто встречающихся нагрузок.

а) сосредоточенная сила (рис. 49):

Рис. 49

при z£a Ф_Q(z)=0

Ф_М(z)=0

при z³a Ф_Q(z)=-P

Ф_М(z)=-P(z-a)

б) распределенная нагрузка (рис. 50):

Рис. 50

при z£c Ф_Q(z)=0

Ф_М(z)=0

при z³c Ф_Q(z)=-q(z-c)

Ф_М(z)=-q(z-c)²/2

в) сосредоточенный момент (рис. 51):

Рис. 51

при z£b Ф_Q(z)=0

Ф_М(z)=0

при z³b Ф_Q(z)=0

Ф_М(z)=-L

Пример

Для заданной схемы нагружения стержня (рис. 52) построить эпюры поперечной силы Q_y(z) и изгибающего момента M_x(z) при следующих исходных данных:

L = 5 кНм, P = 10 кН, q = 20 кН/м, l = 1 м.

Рис. 52

Решение

Запишем уравнения поперечных сил и изгибающего момента:

Q_y (z) = Q_y(0) │₁ – P - q×(z - l) │₂

M_x (z) = M_x (0) + Q_y(0)×z│₁ - P×(z - l) - q×(z - l)²/2│₂

В соответствии с условиями закрепления стержня запишем граничные условия в следующем виде: M_x (0) = - L,

M_x (3l) = 0.

Для нахождения неизвестной реакции Q_y (0) необходимо приравнять уравнение изгибающего момента к нулю при координате z = 3l:

M_x (3l) = M_x (0) + Q_y (0)×3l - P×(3l - l) - q×(3l - l)²/2 = 0.

Решая это уравнение относительно Q_y (0), получим Q_y (0) = 21.67кН.

Теперь, учитывая найденные константы, уравнения интегральных характеристик можно переписать в следующем виде:

Q_y (z) = 21.67│₁ – P – q×(z - l) │₂

M_x (z) = -L + 21.67z│₁ – P×(z - l) – q×(z - l)²/2│₂

Построение графиков будем производить аналогично примеру 1.

1 участок 0 ≤ z ≤ l:

Q_y (0) = 21.67 кН,

Q_y (l) = 21.67 кН,

M_x (0) = -5 кНм,

M_x (l) = -5 + 21.67*1 = 16.67 кНм.

2 участок l ≤ z ≤ 3l:

Q_y (l) = 21.67 – 10 = 11.67 кН,

Q_y (3l) = 21.67 – 10 – 20*(3 - 1) = -28.33 кН,

M_x (l) = -5 + 21.67*1 – 10(1 – 1) – 20(1 – 1) = 16.67 кНм,

M_x (3l) = -5 + 21.67*3 – 10(3 – 1) – 20(3 – 1) =0 кНм.

Определим координаты экстремума и значения функции изгибающего момента в экстремальной точке:

Q_y (z1) = 21.67 – P – q (z1 - l) = 0 → z1 = 1.58 м.

M_x (1.58) = -L + 21.67·1.58 – P (1.58 - l) – q (1.58 - l)²/2 = 20.07 кНм.

По рассчитанным значениям строятся графики поперечной силы и изгибающего момента (см. рис. 52).

Дата добавления: 2018-11-24; просмотров: 455; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 9 10 11 12 131415 16 17 18 Следующая ⇒

Мы поможем в написании ваших работ!