Пример 3 . Найти объём усечённого конуса, образованного вращением
прямой y = x + 1 вокруг оси OX и ограниченной линиями
x = 0 и x = 3 .
Решение . В соответствии с выше приведенной формулой имеем:

1. Если точка движется по некоторой кривой и абсолютная величина скорости ее 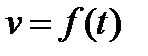 есть известная функция времени t, то путь, пройденный точкой за промежуток времени
есть известная функция времени t, то путь, пройденный точкой за промежуток времени  , равен
, равен  .
.
2. Работа переменной силы  , действующей в направлении от Ох, на отрезке
, действующей в направлении от Ох, на отрезке  определяется формулой
определяется формулой  . При решении задач на вычисление работы силы часто используется закон Гука: F=kx, где
. При решении задач на вычисление работы силы часто используется закон Гука: F=kx, где
F – сила, Н;
x – абсолютное удлинение пружины, м, вызванное силой F;
k – коэффициент пропорциональности.
3. Сила давления воды Р на вертикальную пластину вычисляется по формуле:
 , где
, где
9807Н – вес воды в объеме 1м3;
х – изменение глубины погружения площадки на малую величину dx;
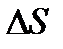 - площадь выделенной площадки;
- площадь выделенной площадки;
(в – а) м. – высота площадки.

Содержание работы
1.Вычислить площадь фигуры, ограниченной линиями: 
2.Скорость движения точки v=12t-3t2 (м/c). Найти путь, пройденный точкой за 3с, за 3-ю секунду, до остановки.
3.Какую работу нужно затратить, чтобы растянуть пружину на 10 мм, если сила в 100 Н растягивает пружину на 0,02 м?
4.Вычислить силу давления воды на вертикальную площадку, имеющую форму треугольника с основанием 4м и высотой 6м. Вершина треугольника находится на поверхности воды, а основание параллельно ей.
|
|
|
Практическая работа №9
Вариант 1
Тема. Решение дифференциальных уравнений с разделяющимися переменными.
Цель. Сформировать умения решать дифференциальные уравнения с разделяющимися переменными.
Методические указания
Определения:
Дифференциальным уравнением называется равенство, содержащее производные или дифференциалы неизвестной функции.
Функция, удовлетворяющая дифференциальному уравнению, т.е. обращающая его в тождество, называется интегралом или решением этого уравнения.
Рассмотрим дифференциальные уравнения вида
Уравнение вида  ; где f ( x ),
; где f ( x ),  -данные функции, называется уравнением с разделёнными переменными.
-данные функции, называется уравнением с разделёнными переменными.
Решение, содержащее произвольную постоянную с, называется общим решением дифференциального уравнения.
Решение, в которое поставлено конкретное числовое с, называется частным решением. Значение с вычисляется при подстановке начальных данных в общее решение.
Уравнение вида  ;
;
где 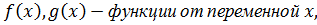

Называется уравнением с разделяющимися переменными.
|
|
|
Задача нахождения решения дифференциального уравнения, удовлетворяющего условию  Пример 1.
Пример 1.
Решить дифференциальное уравнение  .
.
Решение:
Это дифференциальное уравнение с разделяющимися переменными.
Заменим  :
:
 если у≠1, то
если у≠1, то 



Это и есть решение заданного дифференциального уравнения в явном виде.
Пример 2.
Решить дифференциальное уравнение  .
.
Решение:
Это также дифференциальное уравнение с разделяющимися переменными.
 если у≠1, то
если у≠1, то 


потенцируем  обозначим
обозначим  - это общее решение заданного дифференциального уравнения.
- это общее решение заданного дифференциального уравнения.
Содержание работы
1. а) Докажите, что функция  удовлетворяет дифференциальному уравнению
удовлетворяет дифференциальному уравнению 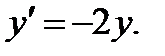
б*) Проверьте, что функция  является решением дифференциального уравнения
является решением дифференциального уравнения 
2. Решите дифференциальные уравнения:
а) 
б) 
3. Найдите частные решения дифференциальных уравнений:
а) 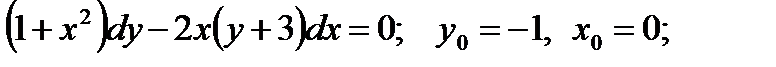
б)* 
в)* 
Практическая работа №10
Вариант I
Тема: Решение однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
Цель: Сформировать умение решать однородные линейные уравнения II порядка с постоянными коэффициентами.
Методические указания
Линейным однородным дифференциальным уравнением второго порядка называется уравнение вида
|
|
|
Y''+py'+gy=0, p,g - постоянные величины
Для решения заменяем
y''=к2 , y'=k, y=1 k2+pk+g=0
возможны 3 случая:
1)D>0; k1≠k2
Общее решение: y=c1 ek1 x + c2 ek2 x
2)D=0; k1=k2=k
Общее решение: y=ekx (c1 +c2 x)
3) D<0; K1=a+bi ,K2=a-bi
Y= eax (c1 cosbx+c2 sinbx)-общее решение
Пример 1. Решить уравнение  .
.
Решение. Дискриминант этого квадратного уравнения  , поэтому
, поэтому  .
.
Покажем, как по виду корней характеристического уравнения найти общее решение однородного линейного уравнения второго порядка.
Если  - действительные корни характеристического уравнения, то
- действительные корни характеристического уравнения, то  .
.
Если корни характеристического уравнения одинаковы, т.е.  , то общее решение дифференциального уравнения ищут по формуле
, то общее решение дифференциального уравнения ищут по формуле  или
или  .
.
Если же характеристическое уравнение имеет комплексные корни  , то
, то  .
.
Пример 2. Найти общее решение уравнения  .
.
Решение.Составим характеристическое уравнение для данного дифференциального уравнения:  . Его корни
. Его корни  ,
, 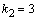 действительны и различны. Поэтому общее решение
действительны и различны. Поэтому общее решение  .
.
Пример 3. Решить уравнение  .
.
Решение. Характеристическое уравнение  или
или  имеет корни
имеет корни  . Так что
. Так что  .
.
Пример 4. Решить уравнение  .
.
Решение. Характеристическое уравнение  данного однородного линейного уравнения мы уже решили выше в примере 4. Корни этого уравнения
данного однородного линейного уравнения мы уже решили выше в примере 4. Корни этого уравнения  , поэтому общее решение линейного однородного уравнения
, поэтому общее решение линейного однородного уравнения
|
|
|
Содержание работы
1)Найти частные решения дифференциальных уравнений:
a) y'' + y' – 6y=0; y0 = 3, x0 =0, y'0 =1
b) y'' – 6y' +9y=0; y0=1; y0' =1; x0 =0
2)Решить уравнение:
a) y'' + 2y'+2y=0
b) y'' + 7y'+6y=0
Практическая работа № 11
Вариант 1
Тема: Применение численного интегрирования в приближенных вычислениях.
Цель: Научиться вычислять определенные интегралы методом прямоугольников и трапеций.
Методические указания
1. Чтобы найти приближенное значение интеграла  методом прямоугольников, нужно:
методом прямоугольников, нужно:
1) разделить отрезок интегрирования [a ; b] на п равных частей точками х0=а, х1, х2, …, хп-1, хп= b ;
2) вычислить значения подынтегральной функции y = f ( x ) в полученных точках: y 0 = f ( x 0 ), y 1 = f ( x 1 ), y 2 = f ( x 2 ), …, yn -1 = f ( xn -1 ), yn = y ( xn );
3) воспользоваться формулой 
2. Чтобы найти приближенное значение интеграла  по формулам трапеций, нужно:
по формулам трапеций, нужно:
1) разделить отрезок интегрирования [a ; b] на п равных частей точками х0=а, х1, х2, …, хп-1, хп= b ;
2) вычислить значения подынтегральной функции y = f ( x ) в полученных точках: y 0 = f ( x 0 ), y 1 = f ( x 1 ), y 2 = f ( x 2 ), …, yn -1 = f ( xn -1 ), yn = y ( xn );
3) воспользоваться формулой 
Пример 1. Вычислить по формуле прямоугольников  . Найти абсолютную и относительную погрешности вычислений.
. Найти абсолютную и относительную погрешности вычислений.
Решение:
Разобьём отрезок [a, b] на несколько (например, на 6) равных частей. Тогда а = 2, b = 5 , 
х0 = 2=a
х1 =  2 +
2 +  = 2,5
= 2,5
х2 =  = 2,5+
= 2,5+  =3
=3
х3 = 3 +  = 3,5
= 3,5
х4 = 3,5+  = 4
= 4
х5 = 4+  = 4,5
= 4,5
f (x0) = 22 = 4
f (x 1 ) = 2 ,5 2 = 6,25
f (x 2 ) = 32 = 9
f (x 3 ) = 3,52 = 12,25
f (x 4 ) = 42 = 16
f (x 5 ) = 4,52 = 20,25.
| х | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 |
| у | 4 | 6,25 | 9 | 12,25 | 16 | 20,25 |
По формуле (1):

Для того, чтобы вычислить относительную погрешность вычислений, надо найти точное значение интеграла:



Содержание работы
1. Вычислите по формуле прямоугольников и трапеций  , с точностью до 0,001, разбив интервал интегрирования на 10 частей.
, с точностью до 0,001, разбив интервал интегрирования на 10 частей.
2. Вычислите интеграл  по формуле прямоугольников и трапеций, разбив промежуток интегрирования на 10 равных частей.
по формуле прямоугольников и трапеций, разбив промежуток интегрирования на 10 равных частей.
3. Вычислите интеграл  по формуле прямоугольников, разбив промежуток интегрирования на 5 равных частей.
по формуле прямоугольников, разбив промежуток интегрирования на 5 равных частей.
Проверьте полученные результаты, вычислив данные интегралы методом замены переменной.
Практическая работа №12
Вариант 1
Тема. Выполнение действий над матрицами.
Цель. Научиться выполнять действия над матрицами.
Методические указания
Произвольная система чисел из некоторого множества, расположенная в виде прямоугольной таблицы, содержащей m строк и n столбцов, называется матрицей.


Две матрицы называются равными, если число строк и столбцов у них соответственно равны.
Если число строк матрицы равно числу её столбцов, то такая матрица называется квадратной, а это число порядком матрицы.
В =  - матрица третьего порядка
- матрица третьего порядка
Пусть даны матрицы
А =  и В =
и В = 
Произведением А на число с называется матрица
С = 
Пример 1.

Суммой матриц А и В называется матрица:
С = А + В = 
Пример 2.
А =  В =
В =  А + В =
А + В = 
Для матриц выполняются все свойства действий с рациональными числами.
Произведением матрицы А на матрицу В называется матрица
С =  , где
, где

Пример 3.

Квадратная матрица, все диагональные элементы которой равны 1, а остальные 0 называется единичной.
Е =  .
.
Матрицы, имеющие вид 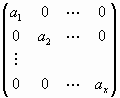 называют диагональными.
называют диагональными.
Матрица, которая получается из данной матрицы заменой строк столбцами, называется транспонированной по отношению к данной.
Содержание работы
1. Вычислить линейные комбинации матриц:
а) 2А-В, если

б) 3А+2В, если
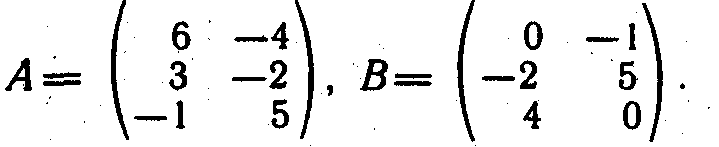
в) 2А+ 3 В -C, если

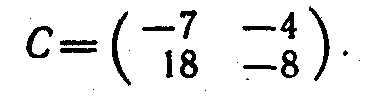
2.Вычислить С=А2+2В, где

3.Найти АВ-ВА, где

4.Найти  , если
, если

Практическая работа №13
Вариант 1
Тема. Выполнение действий над определителями матриц.
Цель. Научиться выполнять различные действия над определителями.
Методические указания
 .- определитель 2 порядка
.- определитель 2 порядка
Пример 1.


Определитель 3 порядка
Пример 2.

Минором  к элементу
к элементу  определителя
определителя  -го порядка называется определитель
-го порядка называется определитель  -го порядка, полученный из исходного вычеркиванием
-го порядка, полученный из исходного вычеркиванием  -той строки и
-той строки и  -того столбца.
-того столбца.
Пример 3. Найти минор  к элементу
к элементу 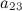 определителя
определителя  .
.
Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:

тогда 
Ответ. 
Алгебраическое дополнение
Алгебраическим дополнением  к элементу
к элементу  определителя
определителя  -го порядка называется число
-го порядка называется число 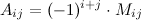
Пример4. Найти алгебраическое дополнение 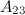 к элементу
к элементу 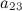 определителя
определителя  .
.
Решение. 
Ответ: 
Содержание работы
1. Вычислить определители второго порядка: 
2. Вычислить определители третьего порядка: 
3. Записать все миноры определителя: 
4. Записать все алгебраические дополнения определителя: 
5. Вычислить определитель разложением его по элементам: а) второй строки, б) третьего столбца:  .
.
Практическая работа №14
Вариант 1
Тема. Решение систем линейных уравнений по формулам Крамера.
Цель. Научиться решать системы линейных уравнений по формулам Крамера.
Методические указания
1. Система двух линейных уравнений с двумя переменными
 при условии, что
при условии, что 
имеет единственное решение, которое находится по формулам:
 ;
;  .
.
2. Система трёх линейных уравнений с тремя переменными
 при условии, что
при условии, что 
имеет единственное решение, которое находится по формулам
 ;
;  ;
;  .
.
Пример 1.
Решить систему уравнений:

относительно переменных х и у.
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы :

Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:

Сделаем аналогичное действие, заменив в первом определителе второй столбец:

Применим формулы Крамера и найдем значения переменных:
 и
и  .
.
Ответ: 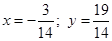
Пример2 .
Решить систему по формулам Крамера.

Решение :
Решим систему по формулам Крамера.

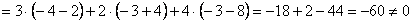 , значит, система имеет единственное решение.
, значит, система имеет единственное решение.






Ответ :  .
.
Содержание работы
1. Решите систему уравнений с помощью формул Крамера:
1)  2)
2) 
2. Решите систему уравнений с помощью определителей:
1)  2)
2) 
Практическая работа №15
Тема:Решение систем уравнений методом Гаусса.
Цель: Научиться решать системы линейных уравнений матричным методом.
Методические указания
Пусть 
 .
.
1) Запишем расширенную матрицу, состоящую из коэффициентов при переменных
х, y , z и свободных членов.
2) Приведем полученную матрицу к треугольному виду, пользуясь следующими преобразованиями:
· умножение или деление коэффициентов и свободных членов на одно и то же число;
· сложение и вычитание строк матрицы;
· перестановка строк матрицы.
3) Запишем новую эквивалентную систему уравнений: 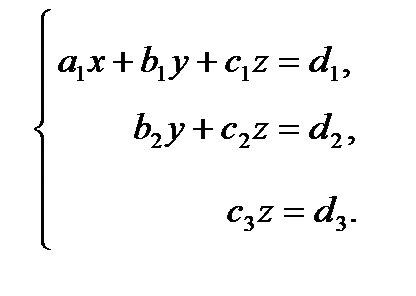

4) Последовательно решим уравнения относительно переменных.
Содержание работы
Решите системы уравнений методом Гаусса:

.
Практическая работа №16
Вариант 1
Тема: Выполнение действий над комплексными числами, заданными в алгебраической форме.
Цель: Научиться выполнять действия над комплексными числами.
Методические указания
1. Понятие мнимой единицы:  , i – мнимая единица.
, i – мнимая единица.
2. Числа вида  , где а, b – действительные числа, i - мнимая единица, называются комплексными. a – действительная часть, bi – мнимая часть.
, где а, b – действительные числа, i - мнимая единица, называются комплексными. a – действительная часть, bi – мнимая часть.
3. Действия над комплексными числами в алгебраической форме
Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами.
Пример 1. Даны комплексные числаz1 = 2 + 3i, z2 = 5 – 7i. Найти:
а) z1 + z2; б) z1 – z2; в) z1z2.
Решение.
а) z1 + z2 = (2 + 3i) + (5 – 7i) = 2 + 3i + 5 – 7i = (2 + 5) + (3i – 7i) = 7 – 4i;
б) z1 – z2 = (2 + 3i) – (5 – 7i) = 2 + 3i – 5 + 7i = (2 – 5) + (3i + 7i) = – 3 + 10i;
в) z1z2 = (2 + 3i)(5 – 7i) = 10 – 14i + 15i – 21i2 = 10 – 14i + 15i + 21 = (10 + 21) + (– 14i +15i) = 31 + i
(здесь учтено, что i2 = – 1).Два комплексных числа называются сопряженным, если они отличаются друг от друга только знаками перед мнимой частью.
Произведение двух сопряженных чисел всегда равно действительному числу. Воспользуемся этим свойством для выполнения деления двух комплексных чисел. Чтобы выполнить деление, произведем дополнительное действие: умножим делимое и делитель на комплексное число, сопряженное делителю.
Пример 2. Выполнить деление:
Решение. Имеем 
Произведем умножение для делимого и делителя в отдельности:
(2 + 3i)(5 + 7i) = 10 + 14i + 15i + 21i2 = – 11 + 29i;
(5 – 7i)(5 + 7i) = 25 – 49i2 = 25 + 49 = 74.Итак,

Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен.
Пример 3. Решите уравнение
x2 – 6x + 13 = 0;
Решение. а) Найдем дискриминант по формуле
D = b2 – 4ac.
Так как a = 1, b = – 6, c = 13, то
D = (– 6)2 – 4*1*13 = 36 – 52 = – 16;

Корни уравнения находим по формулам

Мы видим, что если дискриминант квадратного уравнения отрицателен, то квадратное уравнение имеет два сопряженных комплексных корня.
Содержание работы
1. Вычислить:


2. Найти значения хи уиз равенств:

3. Выполнить действия:
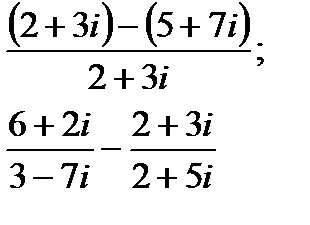
4. Решить квадратные уравнения:

Практическая работа № 17
Вариант 1
Тема: Выполнение действий над комплексными числами ,заданными в тригонометрической и показательной форме.
Цель: Научиться выполнять действия над комплексными числами в тригонометрической и показательной форме.

Практическая работа №18
Вариант 1
Тема. Решение задач с элементами комбинаторики.
Цель. Сформировать умение решать задачи с элементами комбинаторики.
Методические указания
Произведение всех натуральных чисел от 1 до n включительно называют
n-факториалом и пишут n!=1×2×3…(n-1)×n
Pn=n! Pn- перестановка из n элементов.
 А - размещение. А - размещение.
 С - сочетания.
Пример1. Сколькими способами 7 книг разных авторов можно расставить на полке в один ряд?
Перестановками называют комбинации, состоящие из одних и тех же п различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок обозначается Рп и оно равно п!, т.е. Рп = п!, где п! = 1 * 2 * 3 * … п.
Решение: Р7 = 7!, где 7! = 1 * 2 * 3 * 4 * 5 * 6 * 7 =5040, значит существует 5040 способов осуществить расстановку книг.
Ответ: 5040 способов.
Размещения – соединения, содержащие по m предметов из числа n данных, различающихся либо порядком предметов, либо самими предметами; число их.
В комбинаторике размещением называется расположение “предметов” на некоторых “местах” при условии, что каждое место занято в точности одним предметом и все предметы различны.
В отличие от сочетаний размещения учитывают порядок следования предметов. Так, например, наборы < 2,1,3 > и < 3,2,1 > являются различными, хотя состоят из одних и тех же элементов {1,2,3} (то есть, совпадают как сочетания).
Пример2. Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны? Это пример задачи на размещение без повторений.
Размещаются здесь десять цифр по 6. Значит, ответ на выше поставленную задачу будет: С - сочетания.
Пример1. Сколькими способами 7 книг разных авторов можно расставить на полке в один ряд?
Перестановками называют комбинации, состоящие из одних и тех же п различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок обозначается Рп и оно равно п!, т.е. Рп = п!, где п! = 1 * 2 * 3 * … п.
Решение: Р7 = 7!, где 7! = 1 * 2 * 3 * 4 * 5 * 6 * 7 =5040, значит существует 5040 способов осуществить расстановку книг.
Ответ: 5040 способов.
Размещения – соединения, содержащие по m предметов из числа n данных, различающихся либо порядком предметов, либо самими предметами; число их.
В комбинаторике размещением называется расположение “предметов” на некоторых “местах” при условии, что каждое место занято в точности одним предметом и все предметы различны.
В отличие от сочетаний размещения учитывают порядок следования предметов. Так, например, наборы < 2,1,3 > и < 3,2,1 > являются различными, хотя состоят из одних и тех же элементов {1,2,3} (то есть, совпадают как сочетания).
Пример2. Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны? Это пример задачи на размещение без повторений.
Размещаются здесь десять цифр по 6. Значит, ответ на выше поставленную задачу будет:  Ответ:151200 способов
Содержание работы
1. Сколько двузначных чисел можно составить из цифр 1, 3, 5, 8, 9 так, чтобы в каждом числе не было одинаковых цифр?
2. Из 6 открыток надо выбрать 3. Сколькими способами это можно сделать?
3. Решить уравнение
Ответ:151200 способов
Содержание работы
1. Сколько двузначных чисел можно составить из цифр 1, 3, 5, 8, 9 так, чтобы в каждом числе не было одинаковых цифр?
2. Из 6 открыток надо выбрать 3. Сколькими способами это можно сделать?
3. Решить уравнение  4. Найти X, если
4. Найти X, если  5. Вычислить:
а)
5. Вычислить:
а)  б ) б )  в)
в)  Практическая работа №19
Вариант 1
Тема: Решение простейших задач на определение вероятностей события.
Цель: Сформировать умения находить вероятность события, используя классическое определение вероятностей и элементов комбинаторики.
Методические указания
1. Основные формулы комбинаторики
Pn=n! Pn- перестановка из n элементов.
Практическая работа №19
Вариант 1
Тема: Решение простейших задач на определение вероятностей события.
Цель: Сформировать умения находить вероятность события, используя классическое определение вероятностей и элементов комбинаторики.
Методические указания
1. Основные формулы комбинаторики
Pn=n! Pn- перестановка из n элементов.
 А - размещение. А - размещение.
 С - сочетания.
2. Классическое определение вероятности события. С - сочетания.
2. Классическое определение вероятности события.
 , где , где 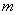 - число благоприятствующих событию - число благоприятствующих событию  исходов, исходов,  - число всех элементарных равновозможных исходов.
Пример1. В классе 30 учащихся. Из них 12 мальчиков, остальные девочки. Известно, что к доске должны быть вызваны двое учащихся. Какова вероятность, что это девочки? Решение:Обозначим событие, вероятность которого надо найти, буквой А. Очевидно, что по условию задачи порядок вызова к доске не играет роли, поэтому N= - число всех элементарных равновозможных исходов.
Пример1. В классе 30 учащихся. Из них 12 мальчиков, остальные девочки. Известно, что к доске должны быть вызваны двое учащихся. Какова вероятность, что это девочки? Решение:Обозначим событие, вероятность которого надо найти, буквой А. Очевидно, что по условию задачи порядок вызова к доске не играет роли, поэтому N=  . Найдём теперь число М благоприятствующих исходов. Для этого следует определить число способов выбора двух девочек из 18. Оно равно . Найдём теперь число М благоприятствующих исходов. Для этого следует определить число способов выбора двух девочек из 18. Оно равно  . По определению вероятности . По определению вероятности  . Свойства вероятностей 1. Вероятность достоверного события равна 1: . Свойства вероятностей 1. Вероятность достоверного события равна 1:  . 2. Вероятность невозможного события равна 0: . 2. Вероятность невозможного события равна 0: 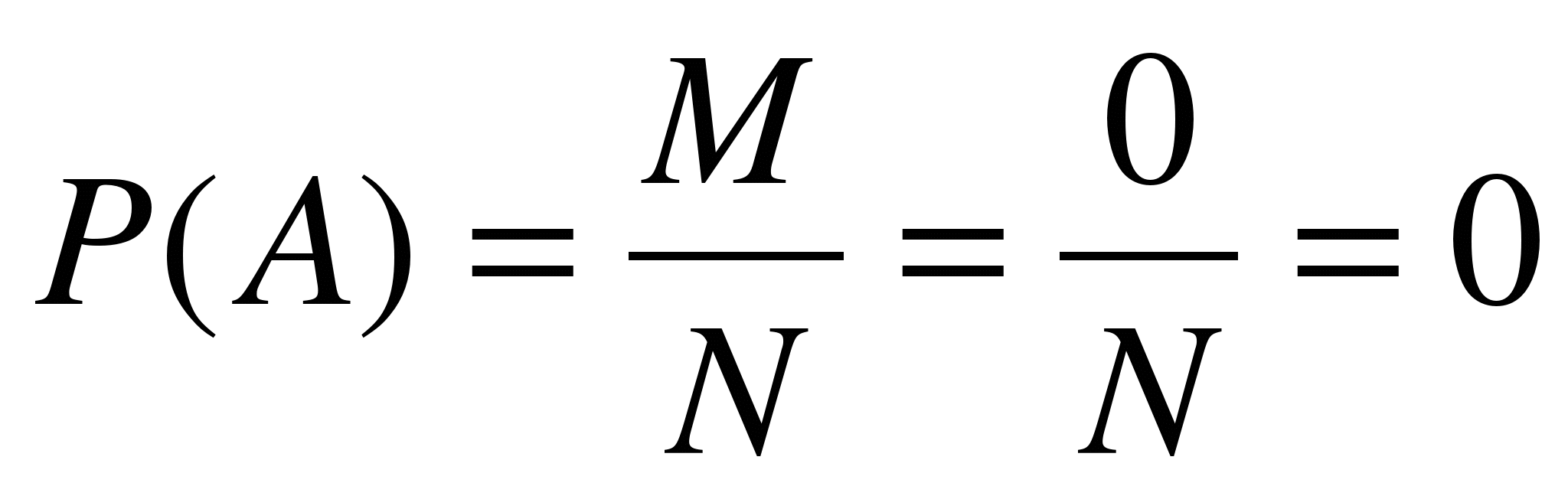 Теорема. Сумма вероятностей противоположных событий равна 1: Теорема. Сумма вероятностей противоположных событий равна 1:  . Вероятность противоположного события находится по формуле: . Вероятность противоположного события находится по формуле:  . Пример2.Вероятность попадания некоторым стрелком по бегущей мишени равна 0,8. какова вероятность того, что этот стрелок промахнётся , сделав выстрел? Решение:Пусть событие А – попадание по мишени, тогда Р(А)=0,8. Событие . Пример2.Вероятность попадания некоторым стрелком по бегущей мишени равна 0,8. какова вероятность того, что этот стрелок промахнётся , сделав выстрел? Решение:Пусть событие А – попадание по мишени, тогда Р(А)=0,8. Событие  - промах. - промах.  = 1-Р(А)=1-0,8=0,2. Ответ:0,2.
Содержание работы
Задача 1.Игральный кубик (кость) бросили один раз. Какова вероятность того, что выпало число очков, больше чем 4.
задача 2.В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 — из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
Задача 3.Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна = 1-Р(А)=1-0,8=0,2. Ответ:0,2.
Содержание работы
Задача 1.Игральный кубик (кость) бросили один раз. Какова вероятность того, что выпало число очков, больше чем 4.
задача 2.В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 — из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
Задача 3.Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 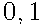 . Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Задача 4.На экзамене по геометрии школьнику достается один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна . Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Задача 4.На экзамене по геометрии школьнику достается один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна  . Вероятность того, что это вопрос на тему «Параллелограмм», равна . Вероятность того, что это вопрос на тему «Параллелограмм», равна  . Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Задача 5.Из урны, в которой находятся 5 белых и 3 черных шара, вынимают один шар. Найти вероятность того, что шар окажется чёрным.
Задача 6. В ящике в случайном порядке разложены 20 деталей, причем 5 из них стандартные. Рабочий берет наудачу 3 детали. Найти вероятность того, что по крайней мере одна из взятых деталей окажется стандартной.
Задача 7.Найти вероятность того, что наудачу взятое двухзначное число окажется кратным либо 3, либо 5, либо тому и другому одновременно. . Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Задача 5.Из урны, в которой находятся 5 белых и 3 черных шара, вынимают один шар. Найти вероятность того, что шар окажется чёрным.
Задача 6. В ящике в случайном порядке разложены 20 деталей, причем 5 из них стандартные. Рабочий берет наудачу 3 детали. Найти вероятность того, что по крайней мере одна из взятых деталей окажется стандартной.
Задача 7.Найти вероятность того, что наудачу взятое двухзначное число окажется кратным либо 3, либо 5, либо тому и другому одновременно.
|
Практическая работа № 20
Вариант 1
Тема: Решение простейших задач на определение дисперсии, математического ожидания и среднего квадратического отклонения случайной величины.
Цель: Сформировать умения находить математическое ожидание и дисперсию случайной величины по заданному закону её распределения.
Методические указания
Математическим ожиданиемдискретной случайной величины называется сумма произведений ее возможных значений на соответствующие им вероятности:
М(Х) = х1р1 + х2р2 + … + хпрп .
Замечание 1. Математическое ожидание называют иногда взвешенным средним, так как оно приближенно равно среднему арифметическому наблюдаемых значений случайной величины при большом числе опытов.
Замечание 2.Из определения математического ожидания следует, что его значение не меньше наименьшего возможного значения случайной величины и не больше наибольшего.
Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата ее отклонения от ее математического ожидания:
D(X) = M (X – M(X))².
Средним квадратическим отклонением σ случайной величины Х называется квадратный корень из дисперсии.
Пример
Закон распределения дискретной случайной величины Х задан в таблице. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
| Условие задачи | |||||
| xi | 2 | 4 | 6 | 8 | 10 |
| pi | 0,2 | 0,3 | 0,1 | 0,2 | 0,2 |
Решение
Расчет ведем по формулам для числовых характеристик дискретных случайных величин.
Математическое ожидание:

Дисперсия:

Среднее квадратическое отклонение:

Содержание работы
1. Даны вероятности значений случайной величины Х: значение 7 имеет вероятность 0,2; значение 1 – вероятность 0,3; значение 5 – вероятность 0,1; значение 4 – вероятность 0,4. Постройте ряд распределения случайной величины Х и определите математическое ожидание, дисперсию.
2. Случайная величина Х характеризуется рядом распределения:
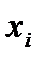
| 0 | 1 | 2 | 3 | 4 |

| 0,2 | 0,4 | 0,3 | 0,08 | 0,02 |
Определите математическое ожидание и дисперсию.
Дата добавления: 2018-11-24; просмотров: 672; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
