Тема: Геометрические и физические приложения производной.
Цель: Отработать навыки применения производной в исследовании физических процессов.
Методические указания
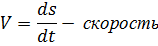
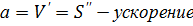
Уравнение касательной к графику 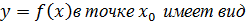
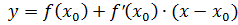
Пример 1. Найти уравнение касательной к графику функции  в точке
в точке 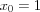
Решение:
1. 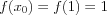
2. 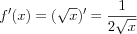
3. 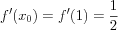
4. 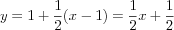
Пример 2.Тело движется прямолинейно по закону 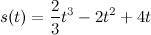 (м). Определить скорость его движения в момент
(м). Определить скорость его движения в момент 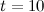 с.
с.
Решение. Искомая скорость - это производная от пути, то есть
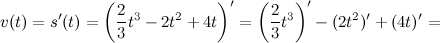
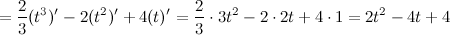
В заданный момент времени
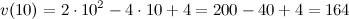 (м/с).
(м/с).
Ответ: 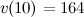 (м/с)
(м/с)
Содержание работы
1) Составить уравнение касательной к графику 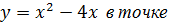
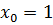 .
.
2) Найдите скорость движения материальной точки в конце 3-й секунды, если движение точки задано уравнением 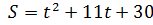 м.
м.
3) Зависимость пути от времени при прямолинейном движении тела массой 12 кг задана уравнением 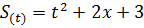 м. Найти кинетическую энергию тела
м. Найти кинетическую энергию тела
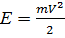 через 5 с после начала движения.
через 5 с после начала движения.
4) Зависимость пути от времени при прямолинейном движении точки задана уравнением 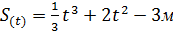 . Вычислить её скорость и ускорение в момент времени t=4 c.
. Вычислить её скорость и ускорение в момент времени t=4 c.
5) Тело массой 4 кг движется по закону 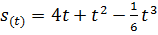 ; S- путь в метрах; t – секунд . Найдите силу, действующую на точку в момент t=20c.
; S- путь в метрах; t – секунд . Найдите силу, действующую на точку в момент t=20c.
6) Стороны а и в прямоугольника изменяются по закону 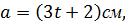
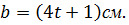 С какой скоростью изменяется его площадь S в момент времени t=2c?
С какой скоростью изменяется его площадь S в момент времени t=2c?
Практическая работа № 4
Вариант 1
Тема: Исследование и построение графиков функций с помощью производной.
Цель: Отработать умения находить с помощью производной промежутки монотонности, выпуклость и вогнутость, точки экстремума и использовать эти исследования при построении графика функции.
|
|
|
Методические указания
При исследовании и построении графиков функций можно использовать следующую схему:
1. Найти область определения функции.
Областью определения (существования) функции D ( y ) называется множество всех действительных значений аргумента х, при которых она имеет действительные значения.
2. Проверить функцию на четность и нечетность.
Функция f называется четной, если для любого х из ее области определения f (- x )= f ( x ). График четной функции симметричен относительно оси ординат.
Функция f называется нечетной, если для любого х из ее области определения f (- x )=- f ( x ). График нечетной функции симметричен относительно начала координат.
3. Найти точки пересечения графика функции с координатными осями:
а) с ОХ: решить уравнение у = 0;
б) с ОУ: решить уравнение х = 0.
4. Найти промежутки знакопостоянства функции. На числовую прямую нанести нули функции и точки разрыва и определить знаки функции в каждом промежутке.
5. Исследовать функцию на монотонность и экстремумы:
|
|
|
· Найти производную 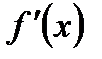 .
.
· Найти критические точки функции, т.е. точки в которых производная обращается в нуль или не существует;
· Исследовать знак производной в промежутках, на которые найденные критические точки делят числовую прямую. Если в некотором промежутке 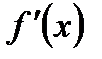 >0, то функция возрастает в этом промежутке; если же
>0, то функция возрастает в этом промежутке; если же 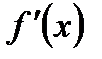 <0, то функция убывает в этом промежутке.
<0, то функция убывает в этом промежутке.
· Выяснить наличие экстремума в каждой критической точке х0, отличной от точек разрыва функции:
1) если 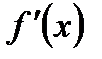 <0 на (а;х0) и
<0 на (а;х0) и 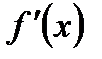 >0 на (х0;в), то х0 – точка минимума функции;
>0 на (х0;в), то х0 – точка минимума функции;
2) если 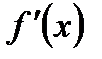 >0 на (а;х0) и
>0 на (а;х0) и 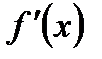 <0 на (х0;в), то х0 – точка максимума функции.
<0 на (х0;в), то х0 – точка максимума функции.
Вычислить значения функции в точках экстремума.
6. Найти контрольные точки.
7. Построить график функции.
8. Найти область значений функции Е(у).
Содержание работы
Исследовать и построить графики функций:
1.y=x2-x
2. y=3x-x3
Практическая работа №5
Вариант 1
Тема. Вычисление неопределённых интегралов методом непосредственного интегрирования.
Цель: Сформировать умения применять таблицу и свойства интегралов для нахождения неопределённых интегралов.
Методические указания
Определение. Если функция 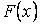 является первообразной для
является первообразной для 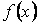 , то выражение
, то выражение 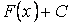 называется неопределённым интегралом от функции
называется неопределённым интегралом от функции 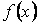 и обозначается символом
и обозначается символом 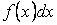 .
.
Таким образом, 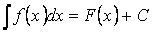 , если
, если 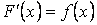
|
|
|
Непосредственным интегрированием называется такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.
Свойства неопределённого интеграла
Свойство 1. Неопределённый интеграл от суммы функций равен сумме неопределённых интегралов 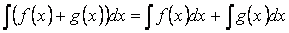
Свойство 2. Неопределённый интеграл от разности функций равен соответствующей разности неопределённых интегралов 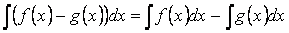
Свойство 3. Постоянный множитель можно выносить за знак интеграла 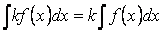
Свойство 4. Если 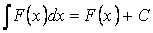 ,то
,то 
Основные формулы интегрирования
1. 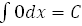
2. 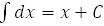
3. 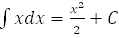
4. 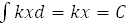
5. 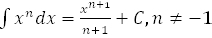
6. 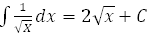
7. 
8. 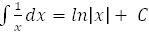
9. 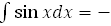 cos x+ C
cos x+ C
10. 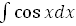 = sin x + C
= sin x + C
11. 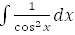 = tgx + C
= tgx + C
12. 
13. 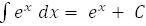
14. 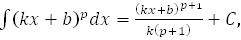 p ≠ -1, k ≠ 0
p ≠ -1, k ≠ 0
15. 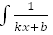 dx=
dx=  ln(kx+b)+C, где k
ln(kx+b)+C, где k 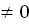
16. 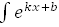 dx=
dx= 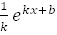 +C, где k
+C, где k 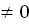
17. 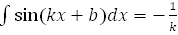 cos(kx+b)+C, где k
cos(kx+b)+C, где k 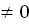
18. 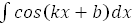 =
= 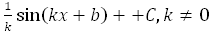
19. 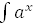 dx=
dx= 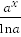 +C, где a
+C, где a 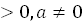
20. 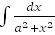 =
= 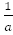 arctg
arctg 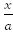 +C, a
+C, a 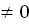
21. 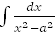 =
= 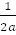 ln│
ln│ 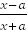 │+ C, a
│+ C, a 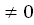
22. 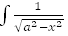 dx=
dx= 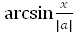 + C, a
+ C, a 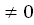
23. 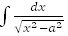 =
= 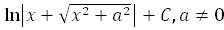
24. 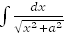 =
= 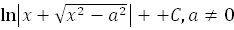
25. 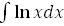 =x ln x
=x ln x 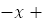 C
C
26. 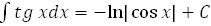
Практическая работа № 6
Вариант 1
Тема: Вычисление неопределенного интеграла методом подстановки и методом интегрирования по частям.
Цель: Отработать навыки вычисления неопределённых интегралов методом подстановки и интегрирования по частям.
|
|
|
Методические указания.
В основе интегрирования методом подстановки лежит формула
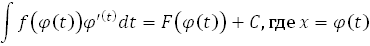
Рассмотрим этот метод.
Алгоритм вычисления неопределенного интеграла методом подстановки:
1. Определяют, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно).
2. Определяют, какую часть подынтегральной функции заменить новой переменной, и записывают эту замену.
3. Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной.
4. Производят замену под интегралом.
5. Находят полученный интеграл.
6. В результате производят обратную замену, т.е. переходят к старой переменной. Результат полезно проверять дифференцированием.
Пример 1.
Вычислить интеграл:
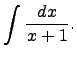
Решение.
Сделаем замену переменных 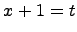 и найдем дифференциал от обеих частей, тогда
и найдем дифференциал от обеих частей, тогда
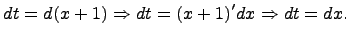
Подставляя все в исходный интеграл, получим:
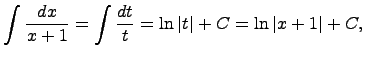
Интегрирование по частям
Другим довольно общим приемом преобразования интеграла является так называемое "интегрирование по частям".
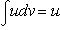
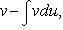 (1)
(1)
Формула (1) называется формулой интегрирования по частям.
Эта формула применяется в случае, когда подынтегральная функция представляет произведение алгебраической и трансцендентной функции.
В качестве u обычно выбирается функция, которая упрощается дифференцированием, в качестве dv - оставшаяся часть подынтегрального выражения, содержащая dx, из которой можно определить v путем интегрирования.
Пример 2.
Найти неопределенный интеграл.
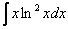
Решение.
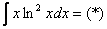
За 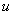 необходимо обозначить логарифм (то, что он в степени – значения не имеет). За
необходимо обозначить логарифм (то, что он в степени – значения не имеет). За 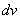 обозначаем оставшуюся часть подынтегрального выражения.
обозначаем оставшуюся часть подынтегрального выражения.
Записываем в столбик:
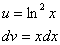
Сначала находим дифференциал 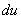 :
:
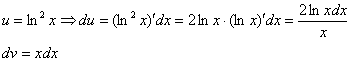
Здесь использовано правило дифференцирования сложной функции 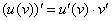 . Теперь находим функцию
. Теперь находим функцию 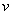 , для этого интегрируем правую часть нижнего равенства
, для этого интегрируем правую часть нижнего равенства 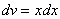 :
:
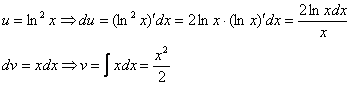
Для интегрирования применили простейшую табличную формулу 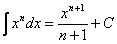
Теперь всё готово для применения формулы 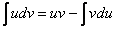 . Открываем «звёздочкой» и «конструируем» решение в соответствии с правой частью
. Открываем «звёздочкой» и «конструируем» решение в соответствии с правой частью 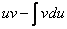 :
:
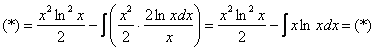
Под интегралом снова многочлен на логарифм! Поэтому решение опять прерывается и правило интегрирования по частям применяется второй раз. Не забываем, что за 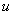 в похожих ситуациях всегда обозначается логарифм.
в похожих ситуациях всегда обозначается логарифм.

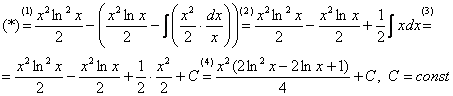
(1) Очень часто здесь теряют минус, также необходимо обратить внимание на то, что минус относится ко всей скобке  , и эти скобки нужно корректно раскрыть.
, и эти скобки нужно корректно раскрыть.
(2) Раскрываем скобки. Последний интеграл упрощаем.
(3) Берем последний интеграл.
(4) Упрощаем ответ.
Необходимость дважды (а то и трижды) применять правило интегрирования по частям возникает не так уж и редко.
Пример 3.
Найти неопределенный интеграл.
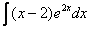
Решение:
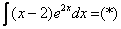
Используя знакомый алгоритм, интегрируем по частям:

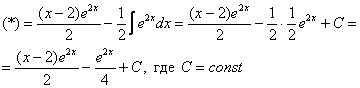
Единственное, что еще можно сделать, это упростить ответ:
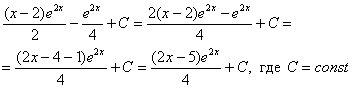
Пример 4.
Найти неопределенный интеграл.
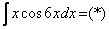
Интегрируем по частям:
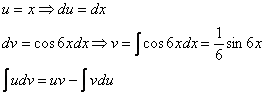
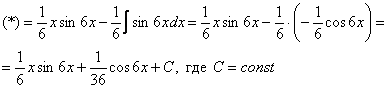
Содержание работы
1. Найти интеграл методом замены переменной:
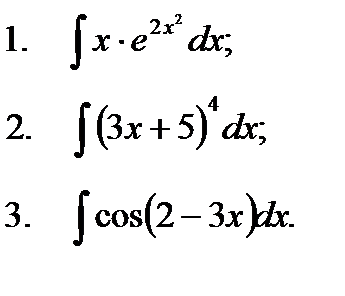
2. Найти интеграл методом интегрирования по частям:
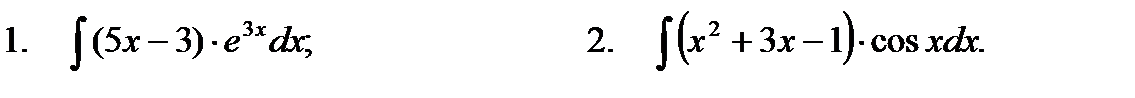
Практическая работа № 7
Вариант 1
Тема: Определенный интеграл.
Цель: Научиться вычислять определенные интегралы.
Методические указания
Формула Ньютона-Лейбница
Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Если F (x) - первообразная функции f (x) на[a, b], то
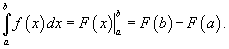
Основные свойства определенного интеграла
I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. 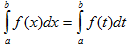 , где х, t – любые буквы.
II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю. , где х, t – любые буквы.
II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.
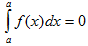 III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.
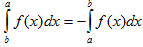 IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
 V. Постоянный множитель можно выносить за знак определенного интеграла.
V. Постоянный множитель можно выносить за знак определенного интеграла.
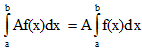 VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
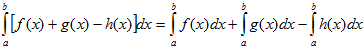
|
Пример 1. Вычислить
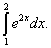
Решение. Используя формулу
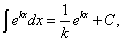
получим
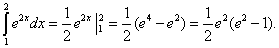
Пример 2.
Вычислить
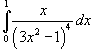 .
Решение.
Сделаем замену: .
Решение.
Сделаем замену:
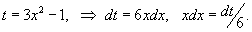 Пересчитаем пределы интегрирования. Если x = 0, то t = −1. Если же x = 1, то t = 2.
Тогда интеграл через новую переменную t легко вычисляется:
Пересчитаем пределы интегрирования. Если x = 0, то t = −1. Если же x = 1, то t = 2.
Тогда интеграл через новую переменную t легко вычисляется:
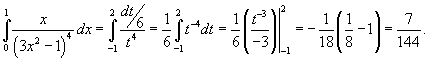
|
Содержание работы
Вычислить определенные интегралы:
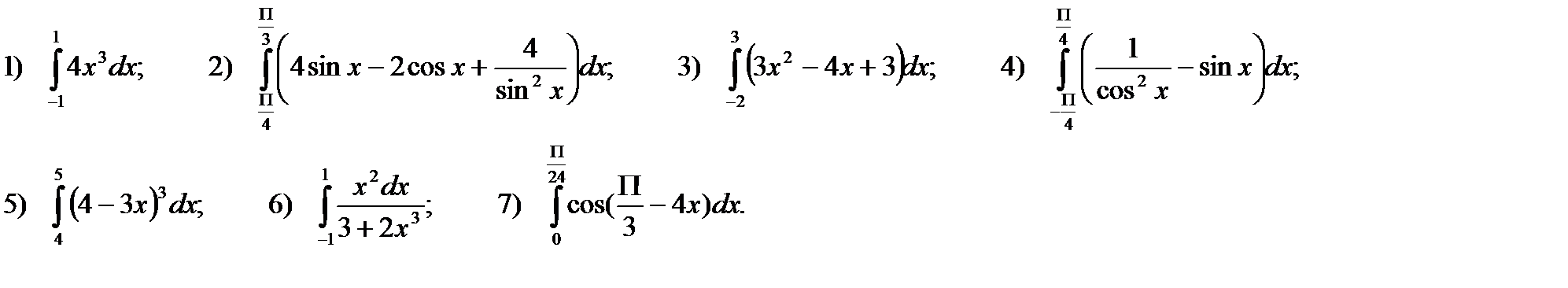
Практическая работа №8
Вариант 1.
Тема. Геометрические и физические приложения определённого интеграла.
Цель: Сформировать умения находить площади фигур, ограниченных графиками рациональных функций.Отработать навыки использования физических приложений определённого интеграла при решении прикладных задач.
Методические указания
Площадь криволинейной трапеции
Площадь фигуры, ограниченной осью 0x, двумя вертикальными прямыми x = a, x = b и графиком функции f (x) (рисунок 1), определяется по формуле
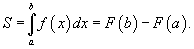

| 
| |
| Рис.1 | Рис.2 |
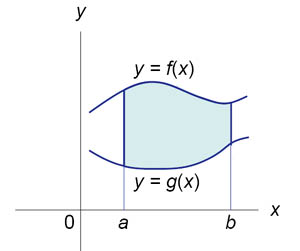
Пусть F (x) и G (x) – первообразные функций f (x) и g (x), соответственно. Если f (x) ≥ g (x) на замкнутом интервале [a, b], то площадь области, ограниченной двумя кривыми y = f (x), y = g (x) и вертикальными линиями x = a, x = b (рисунок 2), определяется формулой
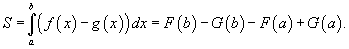
Пример 1.
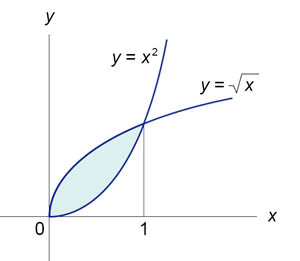
Найти площадь фигуры, ограниченной кривыми 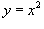 и и 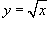 . Решение.
Сначала определим точки пересечения двух кривых (рисунок 3). . Решение.
Сначала определим точки пересечения двух кривых (рисунок 3).
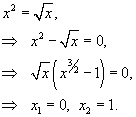 Таким образом, данные кривые пересекаются в точках (0,0) и (1,1). Следовательно,
площадь фигуры равна
Таким образом, данные кривые пересекаются в точках (0,0) и (1,1). Следовательно,
площадь фигуры равна
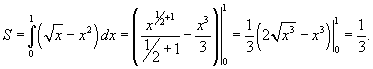
| ||||||
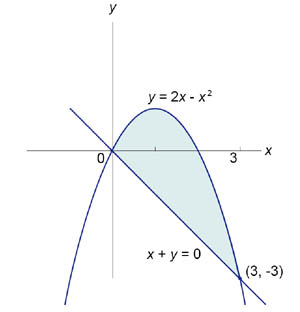
Пример 2.
Найти площадь фигуры, ограниченную графиками функций 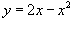 и и 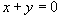 .
Решение.
Найдем координаты точек пересечения кривых (рисунок 4). .
Решение.
Найдем координаты точек пересечения кривых (рисунок 4).
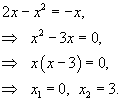 Данная область ограничивается сверху параболой Данная область ограничивается сверху параболой 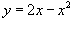 ,
а снизу - прямой линией ,
а снизу - прямой линией 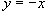 . Следовательно, площадь этой области равна . Следовательно, площадь этой области равна
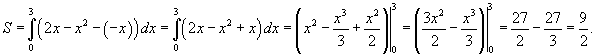
|
Объём тела вращения. Рассмотрим тело, полученное вращением вокруг оси OX криволинейной трапеции, ограниченной графиком функции f ( x ),прямыми x = a и x = b и осью OX ( рис.1 ).
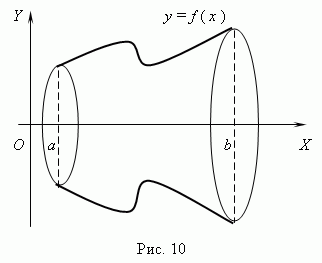
Объём V тела вращения будет равен: 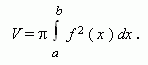
Дата добавления: 2018-11-24; просмотров: 1281; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!