Как исследовать функцию на непрерывность?

Nbsp;

Методические рекомендации

По выполнению практических работ по дисциплине « Математика»

Для обучающихся по техническим специальностям

( базовый уровень)

2018 г

 

 

Методические рекомендации составлены в соответствии с требованиями ФГОС СПО и методическими рекомендациями по реализации основной профессиональной образовательной программы в образовательных учреждениях среднего профессионального образования .

 

 

Автор: ____________

Рецензенты: _______________

                 _______________ 

 

 

Рассмотрены на цикловой комиссии математических , естественно-научных дисциплин и специальности ________________________________

Протокол от «____»__________ 2018 г №_______

Председатель ЦК ______________ Баранова О.И.

Рекомендованы методическим советом

Протокол от «_____»_________2018 г №________

Председатель МС ______________ Е.В. Омутова

Содержание

Пояснительная записка………………………………………………………………..3

 

Практическая работа №1 Исследование функции на непрерывность и вычисление пределов функций ……………………………………………………………………4

 

Практическая работа №2 Вычисление производных сложных функций и функций нескольких переменных………………………………………………………………9

 

Практическая работа№3Геометрические и физические приложения производной…………………………………………………………………………..12   

 

Практическая работа № 4 Исследование и построение графиков функций с помощью производной……………………………………………………………….14

 

Практическая работа №5 Вычисление неопределённых интегралов методом непосредственного интегрирования…………………………………………………16

 

Практическая работа № 6 Вычисление неопределенного интеграла методом подстановки и методом интегрирования по частям………………………………..18

 

Практическая работа № 7 Определенный интеграл……………………………….22

 

Практическая работа №8 Геометрические и физические приложения определённого интеграла…………………………………………………………….25

 

Практическая работа №9 Решение дифференциальных уравнений с разделяющимися переменными……………………………………………………..29

 

Практическая работа №10 Решение однородных дифференциальных уравнений второго порядка с постоянными коэффициентами…………………………….…..31

 

Практическая работа № 11 Применение численного интегрирования в приближенных вычислениях…………………………………………………………33

 

Практическая работа №12 Выполнение действий над матрицами……………….36

 

Практическая работа №13 Выполнение действий над определителями матриц..39

 

Практическая работа №14 Решение систем линейных уравнений по формулам Крамера. ………………………………………………………………………………41

 

Практическая работа №15 Решение систем уравнений методом Гаусса…………43

 

Практическая работа №16 Выполнение действий над комплексными числами, заданными в алгебраической форме…………………………………………………44

Практическая работа № 17 Выполнение действий над комплексными числами , заданными в тригонометрической и показательной форме……………………….47

 

Практическая работа №18 Решение задач с элементами комбинаторики. ………49

 

Практическая работа №19 Решение простейших задач на определение вероятностей события………………………………………………………………..50

 

Практическая работа № 20 Решение простейших задач на определение дисперсии, математического ожидания и среднего квадратического отклонения случайной величины………………………………………………………………………………52

 

Критерии оценки знаний обучающихся…….............................................................55

 

Литература……………………………………………………………………………56

 

 

Пояснительная записка.

Методические указания  по выполнению практических работ по дисциплине «Математика»  составлены в соответствии с Федеральным государственным образовательным стандартом СПО  В них включены примеры и задачи по элементам дифференциального и интегрального исчисления, задания на решения дифференциальных уравнений, а также примеры и задачи по темам: комплексные числа, комбинаторика и элементы теории вероятностей. В каждой теме приводятся основные формулы и краткие теоретические сведения для выполнения соответствующих примеров и задач. Задания сопровождаются подробными решениями .Имеются и необходимые геометрические иллюстрации.

В учебном процессе выделяют два вида самостоятельной работы: аудиторная и внеаудиторная. Аудиторная самостоятельная работа выполняется на учебных занятиях под непосредственным руководством преподавателя и по его заданиям.

Основным видом самостоятельной аудиторной работы являются практические занятия. Методические указания ставят своей целью оказать помощь обучающимся  в выполнении практических работ и способствовать повышению интереса к изучению математики.

Практическая работа №1

Вариант 1

Тема. Исследование функции на непрерывность и вычисление пределов функций.

Цель. Отработать навыки исследования функции на непрерывность и вычисления пределов функций.

Методические указания.

Определение 1. Постоянное число А называется пределом функции f(x) при x→a, если для всякой последовательности {x_n} значений аргумента, стремящейся к а, соответствующие им последовательности {f(x_n)} имеют один и тот же предел А.

Предел функции обозначается .

C войства пределов.

1. Предел суммы

Предел суммы равен сумме пределов, если каждый из них существует, т.е.

2. Предел разности

Предел разности равен разности пределов, если каждый из них существует, т.е.

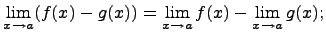
3. Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

4. Предел произведения функции на постоянную величину

Постоянный  коэффициент можно выносить за знак предела:

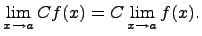
5. Предел произведения Предел произведения равен произведению пределов, если каждый из них существует, т.е.

6. Предел частного

Предел частного равен частному пределов, если каждый из них существует и знаменатель не обращается в нуль, т.е.

7. Предел степенной функции

где степень p - действительное число.

Рассмотрим несколько примеров на свойства пределов.

Пример 1.

 На первом шаге была применена теорема о пределе частного, так как предел знаменателя не равен нулю. На втором шаге использовалась теорема о пределе суммы для числителя и знаменателя дроби. После была применена теорема о пределе произведения.

Пример 2. Найти предел

Знаменатель и числитель дроби при x стремящемся к 2 стремятся к нулю, поэтому теорема о пределе частного здесь неприменима. В таких случаях нужно попытаться упростить дробь. Имеем

Это преобразование справедливо при всех значениях x, отличных от 2, поэтому в соответствии с определением предела можем написать

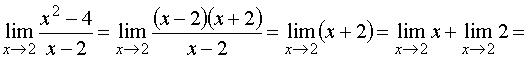
Пределы с неопределенностью вида и метод их решения

Рассмотрим группу пределов, когда 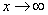, а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены

Пример3.Вычислить предел .

Попытаемся подставить бесконечность в функцию. Что  получается в числителе? Бесконечность. А что получается в знаменателе? Тоже бесконечность. Таким образом,  есть так называемая неопределенность вида .

 

Как решать пределы данного типа?

Итак, метод решения следующий: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на в старшей степени.

 Разделим числитель и знаменатель дроби на :

. Так как 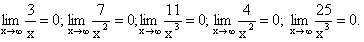, то в результате

 

получим: . Это и есть ответ нашего примера.

Замечание: Предел отношения двух любых целых рациональных функций от х при х стремящимся к бесконечности равен :

1) отношению коэффициентов при высших степенях х , если степени этих функций между собой равны;

2) нулю, если степень числителя ниже степени знаменателя;

3) бесконечности, если степень числителя выше степени знаменателя.

Определение: функция непрерывна в точке , если предел функции в данной точке равен значению функции в этой точке: .

Точка разрыва первого рода

Если в точке нарушено условие непрерывности и односторонние пределы конечны, то она называется точкой разрыва первого рода.

Точки разрыва второго рода

Обычно к данной категории относят все остальные случаи разрыва. Это, когда левосторонний или правосторонний, а чаще, оба предела бесконечны.

Как исследовать функцию на непрерывность?

Исследование функции на непрерывность в точке проводится по схеме, которая состоит в проверке  условий непрерывности:

Пример 1.Исследовать функцию на непрерывность. Определить характер разрывов функции, если они существуют.

Решение:

1) Уделим внимание точке , в которой функция не определена.

2) Вычислим односторонние пределы:

Односторонние пределы конечны и равны.

Таким образом, в точке функция терпит устранимый разрыв.
Ответ: функция непрерывна на всей числовой прямой кроме точки , в которой она терпит устранимый разрыв.

Содержание работы

1. Вычислите пределы, раскрыв неопределённости вида .

а)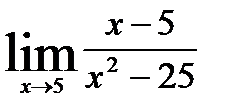

б)

в) .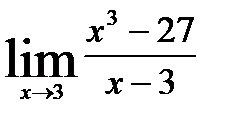

2. Вычислите предел функции на бесконечности:

а)

б)

3. Исследуйте на непрерывность функции: а) y =2 x -1 в точке x =3

                                           б) y = x -3 x ² в точке x = -2

4. Найти точки разрыва функции

 

Практическая работа №2

Вариант 1.

Тема. Вычисление производных сложных функций и функций нескольких переменных

Цель.Отработать умение вычислять производные элементарных и сложных функций, находить частные производные функции z = f ( x ; y ) двух независимых переменных x и y по аргументу x и y .

                                             Методические указания

Формулы дифференцирования

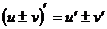
Таблица производных

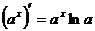
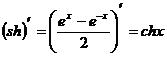
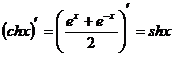
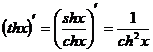
Производная сложной функции

Пусть y– сложная функция x, т.е. y= f(u), u = g(x), или

Если g(x) и f(u) – дифференцируемые функции своих аргументов соответственно в точках x и u= g(x),то сложная функция также дифференцируема в точке xи находится по формуле

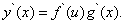
Пример 1. Найти производную функции

Воспользуемся правилом дифференцирования сложной функции.

Находим

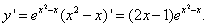
Пример 2. Найти производную функции

Решение.

 Используя свойства логарифмов, данную функцию можно записать проще:

Это сложная логарифмическая функция.

получаем

Для частных производных справедливы все правила дифференцирования и таблица производных элементарных функций. Есть только пара небольших отличий, с которыми познакомимся на примере.

Пример 1.

Найти частные производные первого порядка функции

Найдем частные производные первого порядка. Их две.

Обозначения:
или – частная производная по «икс»
или – частная производная по «игрек»

Начнем с . Когда находим частную производную по «икс», то переменная считается константой (постоянным числом).

Теперь . Когда находим частную производную по «игрек», то переменная считается константой (постоянным числом).

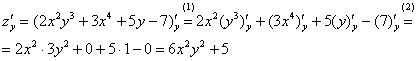
 Дифференциалом функции y = f(x) называется выражение вида dy=A 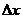- это главная линейная часть приращения ∆y , на основании предыдущей теоремы , обозначив дифференциал независимой переменной через dx=∆x, получим выражение для дифференциала функции:

.

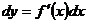Пример 2. Найти дифференциалы функций:

1) ;

2) ;

Решение. Применяя правила дифференцирования степенной и логарифмической функций, находим

1) ;

2) ;

Содержание работы.

I Найти производную сложной функции:

1)

2)

3)

4)

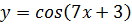
5)

II Найти частные производные функции:

1) -2xy+6x-4 +2

2)

                          

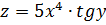
Практическая работа №3

Вариант 1

---

Дата добавления: 2018-11-24; просмотров: 980; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

1234Следующая ⇒

---

Мы поможем в написании ваших работ!