Тема 3.1.3 Построение третьей проекции детали по двум данным. Выполнение необходимых разрезов и сечений.

 

4.3.1 Задание по теме.

 

Построить третье изображение детали по двум данным, выполнить необходимые разрезы и сечения. Построить изображение детали в аксонометрии с вырезом передней четверти детали.

Работу выполнить карандашом на листе формата А3.

 

4.3.2 Порядок выполнения.

 

Изучить основные положения ГОСТ 2.305-68 и 2.317-69, а также рекомендуемую литературу по данной теме. Ознакомиться с заданием (см. приложение А1). Изучить рекомендации по выполнению чертежей и методические указания к данной работе. Ознакомиться с примером выполнения чертежа (рисунок 4.3). Выделить на листе бумаги формата А3 зоны для изображения трех видов и наклонного сечения детали. Нанести тонко карандашом все линии видимого и невидимого контуров, разделяя деталь на основные геометрические части. Нанести все необходимые выносные и размерные линии, построить разрезы и выполнить штриховку в разрезах. Построить горизонтальную проекцию и натуральный вид наклонного сечения. На втором листе формата А3 выполнить наглядное изображение этой детали в прямоугольной изометрии.

 

4.3.3 Методические указания.

 

Изображения предметов на чертеже могут выполняться в прямоугольных (ортогональных) проекциях - видах. Основные виды - вид спереди, вид сверху, вид слева. Для изображения внутренних поверхностей, невидимых на видах применяются разрезы и сечения.

 

Вид –изображение обращенной к наблюдателю видимой части поверхности предмета.Для

 

уменьшения количества изображений допускается на видах показывать необходимые невидимые части поверхности предмета при помощи штриховых линий.

Разрез –изображение предмета,мысленно рассеченного одной или несколькимиплоскостями с удалением передней, отсеченной части и изображением линиями видимого контура того, что получается в секущей плоскости и что расположено за ней.

 

Сечение –изображение фигуры,получившейся при мысленном рассечении предмета однойили несколькими плоскостями, с изображением только того, что попало в секущую плоскость.

 

 

А

 

 

30

А-А ^В                                                                                            Б-Б

10

 

R15

 

Ø20	45	R5	80
50
			32
	15
		40
В		В-В
Б	R10

 

			10
Ø8	10
	Ø20
60			80
	Ø20		Ø20
			2 отв.
10 10	80	10	А		НГЧ. 02.11.004
Б	140				Лит.	МассаМасштаб
			Изм. Лист	№ докум.Подп. Дата	Крышка
			Разраб.	Сидоров К.Н.
			Пров.	Петров С.И.
			Т. контр.		Лист	Листов
			Н. контр.			НИ РХТУ
						шифр 123456
			Утв.

 

Рис. 4.3. Пример выполнения задания

Тема 3.1.4 Построение аксонометрического изображения

 

4.4.1 Задание по теме.

 

Построить изображение детали в аксонометрии с вырезом передней четверти детали. Работу выполнить карандашом на листе формата А3.

4.4.2 Порядок выполнения.

 

Изучить рекомендуемую литературу по данной теме. Изучить рекомендации по выполнению чертежей и методические указания к данной работе. Ознакомиться с примером выполнения чертежа (рисунок 4.4).

 

Аксонометрическое изображение (или сокращенно аксонометрия)представляет собой одиниз видов наглядного изображения объектов, которое получается при параллельном проецировании. Суть этого способа проецирования заключается в том, что данный объект вместе с присоединенными к нему осями прямоугольных координат в пространстве проецируется параллельными лучами на некоторую произвольно выбранную плоскость, называемую плоскостью аксонометрических проекций .

 

Аксонометрические изображения более выразительны, чем прямоугольные на двух или трех плоскостях, так как передают одной проекцией на одной плоскости отображение сразу трех сторон (передней, верхней и левой) объекта, что очень облегчает понимание его действительной формы и ее размеров. Таким образом, аксонометрия представляет собой такое изображение, в котором проекция любой точки в пространстве привязана к аксонометрическим осям, что делает изображение метрически определенным.

 

Отрезки осей присоединенной к объекту системы координат проецируются на плоскость аксонометрических проекций с сокращениями, величина которых зависит от угла между данной осью и плоскостью и называется коэффициентом искажения .

 

Если k - коэффициент искажения по оси Ах , т - по оси Ау и п - по оси А z , то для прямо-

 

угольного аксонометрического изображения при любой ориентации аксонометрических осей сумма квадратов коэффициентов искажения равна двум, т. е. k ² + т ² + п ² = 2.

 

Из возможных вариантов направления проецирования, ориентации аксонометрических осей и соответствующих им коэффициентов, регламентированных стандартом ЕСКД ГОСТ 2.317 - 69*, мы будем использовать только - прямоугольную изометрическую проекцию.

НГЧ. 02.11.004

Лит.

Масса

Масштаб

Изм.

Лист

№ докум.

Подп.

Дата

КРЫШКА

Разраб.

Сидоров К.Н.

Пров.

Петров С.И.

Т. контр.

Лист

Листов

НИ РХТУ

Н. контр.

шифр 123456

Утв.

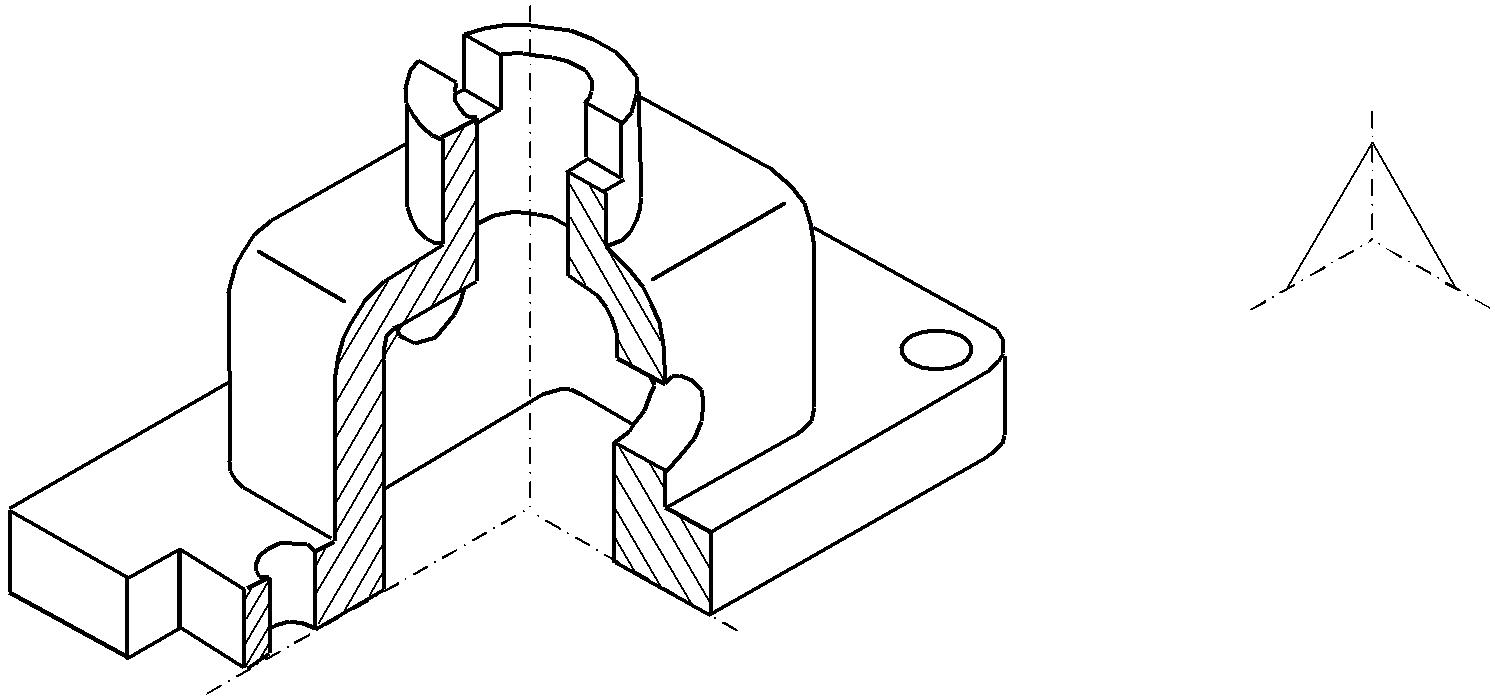
Рис. 4.4. Пример выполнения задания

Изометрическая проекция.Оси присоединенной к объекту системы координат образуют с плоскостью аксонометрических проекций одинаковые углы. Поэтому по всем трем

 

осям коэффициенты искажения равны, т.е. ^{k = m = n =  2}₃ ^{» 0,82} , а также равны углы (120°) между аксонометрическими осями Ах , Ау , А z . Масштаб изометрической проекции равен 1:1. Аксонометрическую оcь А z располагают вертикально.

 

На рисунке 4.5 приведено точное построение осей в изометрии, а на 4.6 - приближенное.

Аz

Аz

 

 

1200	1200
	0			7													7
			4															0	4
Ах		Ау																		Ау
	1200		Ах
Рис. 4.5 - Точное построение			Рис. 4.6 - Приближенное
осей в изометрии			построение осей
						в изометрии

ГОСТ ЕСКД 2.317 - 69* рекомендует с целью упрощения построения принимать зна-чения коэффициентов искажения равными 1 вместо 0,82, что приводит к увеличению изо-метрической проекции в 1,22 раза.

 

Выполнение аксонометрических изображений.Аксонометрию объекта строят по координатам вершин, центров оснований и других характерных точек, входящих в структуру объекта. На аксонометрии отображают контуры отсеков поверхностей, очерковые ребра, очерковые образующие поверхностей вращения.

 

По умолчанию на аксонометрии не отображают части плоскостей и других поверхностей, расположенные внутри контуров отсеков.

 

Линейные размеры формы откладывают только параллельно аксонометрическим осям с учетом коэффициентов искажения.

При необходимости показать отверстия, внутренние полости, выемки и т.п. части формы объекта применяют разрезы. Плоскости разрезов всегда ориентируют параллельно двум осям присоединенной системы координат.

 

Штриховку на разрезах выполняют в соответствии с рисунком 4.7. Направлением штриховки служит одна или другая диагональ квадрата, расположенного в плоскости двух осей присоединенной системы координат.

A_z

1

1

 

 

A_x Ay

 

 

Рис. 4.7 - Штриховка на разрезах аксонометрических изображений

 

На аксонометрическом изображении объекта могут быть нанесены размеры формы по правилам ГОСТ ЕСКД 2.307 - 68*, выносные и размерные линии должны быть расположены параллельно осям присоединенной системы координат. Измерение линейных размеров формы объекта на аксонометрическом изображении выполнимо только в направлениях, параллельных проекциям аксонометрических осей. Измерение размеров формы в других направлениях затруднено тем, что проекции таких размеров формы отличаются от их натуральных величин. Угловые размеры на аксонометрических изображениях не измеряют, так как проекции углов не соответствуют их натуральным величинам.

 

Аксонометрические изображения окружности.Окружность в аксонометрии отображается в виде эллипса. Формы многих геометрических и технических объектов содержат окружности, плоскости которых параллельны двум осям присоединенной к объекту системы координат. Проекции таких окружностей приведены на рисунке 4.8. Для всех окружностей принят условный диаметр d=1. На представляющих собой проекциях окружностей эллипсах нанесены численные значения их больших и малых осей, а также двух сопряженных диаметров, параллельных осям присоединенной системы координат. Над полками линий-выносок указаны значения для практического масштаба, а под полками - для теоретического масштаба. Малая ось каждого эллипса параллельна, а большая - перпендикулярна проекции координатной оси, перпендикулярной плоскости окружности.

 

С целью упрощения выполнения аксонометрических изображений вместо эллипсов рекомендуется строить с помощью циркуля приближенно заменяющие их четырехцентровые овалы, представленные на рисунке 4.9.

		1	Аz	1
0,70		0,82		0,82
				0,70
0,58
				0,58
1				1
0,82				0,82
	1,22			1,22
		1		1
Аx		1,22		Аy
		1
		1		1
		0,82	0,70	0,82
			0,58
Рис. 4.8 - Аксонометрические изображения окружности

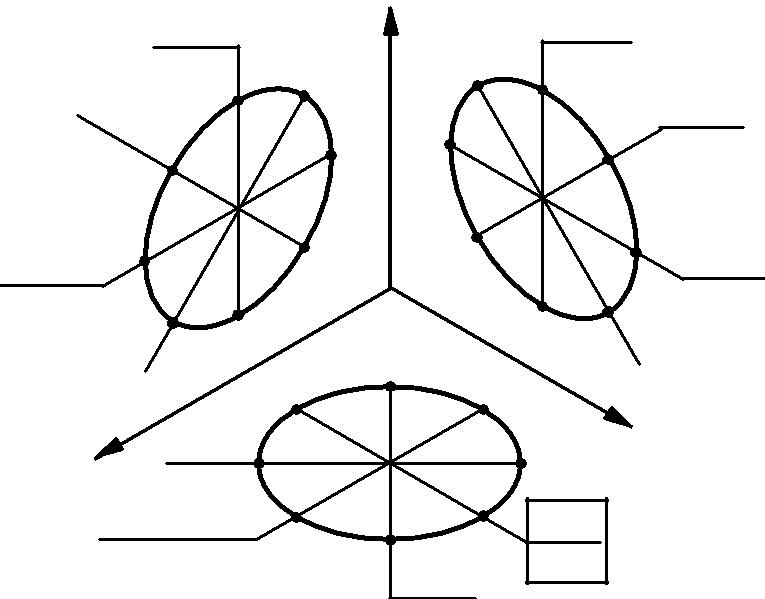
	а)				б)
					А
				а		b
	А6			R	0	R
R2	B5
B3			R1	d		c
	l2			X		У
B2				B4
					В
					А
A3	0	А4		а		b
	l1
				R1	0	R1
B6				C		D
				d		c
	А5			X		У
B1					В

Рис. 4.9 - Построение четырехцентрового овала: а - по размерам; б - вписанного в ромб

 

Оси овалов В 1 и В 2 (рисунок 4.9,а) соответственно равны большим и малым осям эл-липсов. Каждый овал состоит из четырех дуг окружностей ВЗ , 34. В 5, В 6 с центрами А 3, А 4, .А5, А6. Дуги ВЗ и В 4 имеют радиусR1,а дуги В 5 и В6 - радиус R 2. Центры А 3 и А 4 расположены на больших осях В 1 на расстояниях l 1 от центра овала. Центры А 5 и А 6 расположены на малых осях или их продолжениях на расстояниях l 2 от центра овала. Точки соединения дуг окружностей расположены на прямых, проходящих через центры А 3 и А 5, А 3 и А 6, А4 и А 5, А4 и А6. В таблице4.1приведены величины параметров овалов,отображающих окружность с условным диаметром d=1.

Таблица 4.1 - Размеры для построения четырехцентрового овала

 

 

		Размеры				Масштаб
B1	B2	R1	R2	l1	l2
1,22·d	0,7·d	0,26·d	0,96·d	0,35·d	0,61·d	1,22:1

 

На рисунке 4.9,б показано построение овала, вписанного в ромб. Построение строят в следующей последовательности:

 

1) строят ромб со стороной, равной диаметру изображаемой окружности. Через точку 0 проводят изометрические оси и на них от точки 0 откладывают отрезки, равные радиусу изображаемой окружности. Через точки a, b, c и d проводят прямые, параллельные осям; получают ромб. Большая ось овала будет располагаться на большой диагонали ромба;

 

2) вписывают ромб в овал. Для этого из вершин тупых углов (точки А и В) описывают дуги радиусом R, равным расстоянию от вершины тупого угла (точке А или В) до точек a , b или c , d соответственно;

 

3) для определения положения центров малых окружностей из центра 0 проводят дугу, равную радиусу меньшей полуоси овала (касательную к ранее проведенной дуге). Получают точки Си D, которые будут центрами малых дуг;

 

3) через точки В и С, В и D, А и С А и D проводят прямые, которые в пересечении с дугами большого радиуса дают точки сопряжения окружностей;

4) дугами радиуса R1 сопрягают дуги большого овала.

 

Так строят овал, лежащий в плоскости, перпендикулярной к оси Z. Овалы, находящиеся в других плоскостях строят аналогично, причем большая полуось овала всегда перпендикулярна той оси, которая в построении овала не участвует.

Линии пересечения поверхностей тел вращения строят по точкам. Эти точки находятся или по координатам, взятым с ортогональных проекций, или способом вспомогательных секущих плоскостей, непосредственно в аксонометрических изображениях.

Вспомогательные секущие плоскости (рисунок 4.10) пересекают данные цилиндры по образующим линиям.

 

			Аz	1 2 3
	1
		2		3
	1	2		3
	1 2
Аx	3			Аy

 

Рис. 4.10 - Определение точек линии пересечения поверхностей

 

---

Дата добавления: 2018-11-24; просмотров: 1755; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!