Расчет последовательных цепей переменного тока
При отсутствии одного из реактивных сопротивлений все электрические параметры определяются по вышеприведенным формулам. При этом из них нужно исключить параметры с индексом отсутствующего элемента. На рисунке изображена цепь с последовательным соединением. Элемент XС отсутствует, поэтому все формулы упрощаются отсутствием величин емкости.
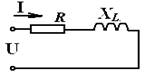
Если схеме имеет несколько одинаковых по характеру элементов, то электрические параметры определяются по формулам, приведенным для цепи с R, ХL, ХС, при этом в них нужно ввести арифметические суммы параметров, имеющих одинаковые индексы.
1. Пример с двумя активными сопротивлениями R1 , R2, индуктивным ХL.
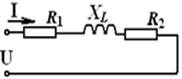
Напряжение, полное сопротивление и полная мощность равны:
U=√ (UR1+UR2)2 + UL2
Z=√ (R1+R2)2+XL2
S=√ (P1+P2)2+QL2
Коэффициент мощности равен:
cos φ = ( UR1 + UR2 ) /U, cos φ = ( R1 + R2 )/ Z, cos φ = ( P1 + Р 2 ) /S
Диаграммы имеют вид:
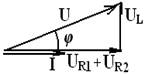

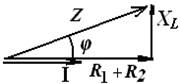
2. Пример решения задачи с двумя активными, индуктивным и емкостным сопротивлениями.
Дано: U = 50 В, R1 = 9 Ом, ХL = 12 Ом, ХС = 27 Ом, R2 = 11 Ом
Определить: Z, I, UR1, UR2, UC, UL, Р, Q, S, cos φ, φ.
Решение.
1. Полное сопротивление цепи равно Z=√ (R1 + R2) 2 + (XL - X C) 2 ,
Z=√ (9 + 11) 2 + (12 - 27) 2 =25 Ом.
2. Ток в цепи равен I = U /Z= 50 В / 25 Ом = 2А.
3. Падение напряжения на активном сопротивлении R1: UR1= I∙R1 =2А∙ 9Ом = =18В
на активном сопротивлении R2: UR2= I∙ R2 = 2 А∙ 11 Ом= 22 В
на индуктивном сопротивлении: UL =I ∙ ХL =2 А ∙12 Ом= 24 В
на емкостном сопротивлении: UС =I ∙ ХС = 2А ∙ 27Ом = 54 В
4. Коэффициент мощности цепи
cos φ= (R2 + R1) / Z= (9+11)Ом /25 Ом= 0,8 или cos φ= UR /U, или cos φ= P / Z
Угол сдвига фаз необходимо найти во избежание потери знака угла (косинус является четной функцией): sin φ= ( XL - XC) /Z = (12 – 27) Ом / 25 Ом = - 0,6
или sin φ = ( UL - UC) /U, или sin φ = ( QL - QC) /S
5. Отсюда угол φ = -36º 52´
6. Активная мощность цепи Р = U I cos φ = 50 В∙ 2 А ∙0,8 = 80 Вт
Можно найти и по формулам Р = Р1 + Р2 = I 2 (R2 + R1)
или Р = Р1 + Р2 = U2R1 / R 1 + U2R2 / R2
или Р = Р1 + Р2 = I∙ (UR1+ UR2 )
7. Определим реактивную мощность Q=S sin φ
или Q = U ∙I ∙ sin φ = 50 В ∙ 2 А ∙ (- 0,6)= - 60 вар
или Q = QL - QC = I 2 (XL - XC)
или Q = I (UL - UC)
или Q = U 2L / XL - U2C / XC
8. Полная мощность цепи S =U I = 50 В ∙2 А= 100 ВА
или по формулам S = I2 Z , или S = U2 / Z, или S =√(Р2 + Q2 ), где Q = QL- QC
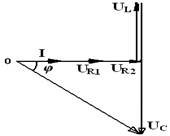
Порядок построения диаграммы
1. Построение векторных диаграмм начинаем с выбора масштаба для тока и напряжения.
m I = 1 А/ см, m U = 5 B/ см. - масштабные коэффициенты, они означают, сколько ампер или вольт содержится в 1 см. Масштаб можно задавать и графически.
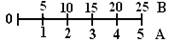
От точки 0 горизонтально вправо проводим вектор тока I общий для всей цепи. В выбранном масштабе его длина будет l I = I / m I= 2 А / (1 А / см)= 2 см.
2. Вектор активного напряжения UR1 совпадает по фазе с током, угол сдвига фаз между ними равен 0, поэтому откладываем его вдоль вектора тока от точки 0 вправо. Его длина l UR1 = UR1 / m U=18 В / (5 В / см)=3,6 см.
3. От конца вектора UR1 откладываем вправо вдоль вектора тока вектор активного напряжения UR2. Его длина l UR2 = UR2 / m U= 22 В / (5 В / см) = 4,4 см.
4. От конца вектора UR2 откладываем вертикально вверх вектор падения напряжения UL на индуктивном сопротивлении, так как он опережает ток на угол 90.
Его длина l U L = UL / m U= 24 см / (5 В/см) = 4, 8 см.
5. От конца вектора UL откладываем вертикально вниз вектор падения напряжения UC на емкостном сопротивлении, так как он отстает от тока на угол 90º.
Его длина l UC = UC / m U=54 В / (5 В/см) = 10, 8 см.
Геометрическая сумма векторов UR1, UR2, UL, UC должна быть равна полному напряжению U, приложенному к зажимам цепи, т. е. U = UR1+ UR2+ UL +UC. Измерив длину этого вектора, убеждаемся, что она l U= 10 см. Это значит, что с учетом масштаба его величина будет U = 10 см. ∙ 5 В/ см = 50 В.
По условию задачи именно такое напряжения приложено к зажимам цепи.
Дата добавления: 2018-11-24; просмотров: 210; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
