МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ №2 ПО ТЕМЕ «ЗАКОНЫ ПЕРЕМЕННОГО ТОКА. ОДНОФАЗНЫЕ И ТРЕХФАЗНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ»

Однофазные электрические цепи

Теория

В этих цепях, так же как и в цепях постоянного тока, при решении задач используют закон Ома, первый закон Кирхгофа, формулы мощности, свойства последовательного и параллельного соединений. Однако из-за того, что в переменном токе действуют три вида совершенно различных по характеру сопротивлений (активное R, индуктивное Х_L и емкостное Xс), форма записи законов изменяется. Иначе устанавливается связь и между однородными электрическими величинами. Так, при последовательном соединении в постоянном токе общее сопротивление было равно арифметической сумме сопротивлений, в переменном токе берется уже геометрическая сумма R , Х_L и Х_С. Геометрически складываются также напряжения и мощности на этих сопротивлениях. В разветвленных цепях постоянного тока первый закон Кирхгофа устанавливал связь между токами в арифметической форме, в переменном токе эта связь будет геометрическая. В связи с особенностями однофазных электрических цепей синусоидального тока рассмотрим, основные соотношения между электрическими величинами для наиболее характерных цепей. Однофазная электрическая цепь переменного синусоидального тока с последовательным соединением активного R, индуктивного Х_L и емкостного X_С сопротивлений.

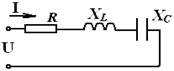
На этой схеме: I = U /Z, A - ток, потребляемый цепью, единица измерения – ампер;
R, 0м - активное сопротивление цепи, единица измерения - Ом;
U_R, В - напряжение на активном сопротивлении, единица измерения - вольт;
Р, Вт - активная мощность цепи, единица измерения - ватт;
Х_L = ωL = 2πf,Oм - индуктивное (реактивное) сопротивление цеди, единица измерения - Ом;
U_L, B - напряжение на индуктивном сопротивлении, единица измерения - вольт;
Q_L , вap - индуктивная (реактивная) мощность, единица измерения вольт-ампер реактивный;
Хс = 1 / ωC= 1 / 2πfC, Ом - емкостное (реактивное) сопротивление цепи, единица измерения - Ом;
Uc , В - напряжение на емкостном сопротивлении, единица измерения - вольт;
Q_С , вap - емкостная (реактивная) мощность, единица измерения -вольт-ампер реактивный;
Z , Ом - полное сопротивление цепи, единица измерения - Ом;
U, В - полное напряжение, подведенное к зажимам цепи, единица измерения - вольт;
S, ВA - полная мощность, единица измерения - вольт-ампер.

Общее решение типовых задач

1. На основании закона Ома напряжения на активном, индуктивном и емкостном сопротивлениях могут быть определены по формулам: U_R = IR, U_L= I Х_L, U_C = I Х_{С .}При этом следует иметь в виду, что U_R - совпадает по фазе с током,
U_L - опережает по фазе ток на 90⁰,
U_C- отстает от тока на 90°.

2. Строим диаграмму напряжений. Результирующее напряжение U представляет геометрическую сумму напряжений U_R, U_L, U_C.

Результирующее напряжение U , которое является напряжением, подведенным к зажимам цепи, можно найти не только графически (в этом случае диаграмма должна быть построена в масштабе), но и математически, на основании теоремы Пифагора: U ² = U_R ² +( U_L - U_C )²

3. Если каждое из напряжений на векторной диаграмме (рис.1) разделить на ток I, то получится фигура, подобная векторной диаграмме, которая будет называться треугольником сопротивлений, т.к. R = U_R / I , Х _L = U_L / I , Х_С = U_C / I , Z = U / I .

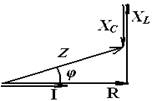
Из треугольника сопротивлений следует, что Z ² = R ² +( X_L - X_C )²

4. Если каждое из напряжений на векторной диаграмме (рис.1) умножить на ток I, то получится фигура, подобная векторной диаграмме, которая будет называться треугольником мощностей, так как Р = U_R I, Q_L= U_L I, Q_C= U_C I, S =U I.

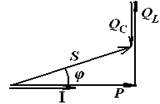
Из треугольника мощностей следует, что S ² = P ² + ( Q_L – Q_C )².

Используя закон Ома для каждого элемента цепи, мощность можно найти:
Р = I ²R
Q_L = I ²X_L
Q_C = I ² X_C
S = I² Z

5.Из треугольника мощностей также следует, что Р = S cos φ или Р = U I cos φ;
Q=S sin φ или Q = U I sin φ где Q = Q_L - Q_C- результирующая реактивная мощность.

6.Анализируя векторную диаграмму напряжений, треугольник сопротивлений, треугольник мощностей, можно сделать вывод, что при U_L >U_C ( X_L > Х_C) результирующий вектор напряжения U опережает вектор тока Iна угол φ < 90°, а при U_L < U_C(X_L < X_C) результирующий вектор напряжения отстает от вектора тока на угол φ. Тригонометрические функции угла сдвига фаз можно записать в виде:
cos φ= U_R /U
cos φ= R / Z
cos φ= P / S
sin φ = ( U_L - U_C) /U
sin φ= ( X_L - X_C) /Z
sin φ = ( Q_L - Q_C) /S.

Величина cos φ называется коэффициентом мощности.

Дата добавления: 2018-11-24; просмотров: 206; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!