Скорость распространения волн
Министерство образования и науки Российской федерации
Федеральное агентство по образованию
Южно-Уральский государственный университет
Филиал в г. Миассе
Кафедра «Гидравлика и теплотехника»
621.311.22
В.Г. Зезин
Нестационарные процессы Гидродинамики
Учебное пособие
Челябинск
Издательство ЮУрГУ
2011
Оглавление
1. Модели нестационарного движения жидкости. 3
1.1. Классификация моделей нестационарного течения. 3
1.2. Скорость распространения волн. 5
1.3. Дифференциальные уравнения нестационарного движения жидкости в трубопроводе. 9
1.4. Волновые уравнения для потока жидкости в длинных трубопроводах. 12
2. Медленно изменяющиеся течения. 18
2.1. Общие свойства и уравнения движения. 18
2.2. Примеры медленно изменяющихся течений. 19
2.2.1. Разгон потока жидкости. 19
2.2.2. Выравнивание уровней жидкости в сообщающихся сосудах. 21
2.2.3. Предельная частота движений поршня насоса. 23
3. Волновые процесы в гидросистеме. 26
3.1. Описание волн. 26
3.2. Взаимодействие волн с различными элементами гидросистемы.. 30
3.2.1. Отражение волны от упругого элемента гидросистемы.. 30
3.2.2. Прохождение волны через дроссель. 35
3.2.3. Прохождение волны через стык трубопроводов различного диаметра 39
3.3. Стоячие волны.. 41
3.4. Гидравлический удар. 43
3.5. Характеристики элементов гидросистем. 47
3.5.1. Характеристики источников питания. 47
3.5.2. Характеристики гидродвигателей. 49
|
|
|
3.5.3. Характеристики регулирующей и распределительной аппаратуры.. 53
3.5.4. Общие замечания по характеристикам элементов гидросистемы.. 56
4. Анализ волновых процессов в гидросистеме методом характеристик. 58
4.1. Общие положения. 58
4.2. Фазовые характеристики волн. 59
4.3. Пример расчета переходного процесса в объемном гидроприводе методом характеристик. 61
4.4. Общий алгоритм расчета переходного волнового процесса в гидросистеме методом характеристик. 71
5. Библиографический список. 74
Модели нестационарного движения жидкости
Классификация моделей нестационарного течения
Нестационарные течения – это течения, при которых параметры потока изменяются по времени. Эти изменения могут происходить медленно, например, при перетекании жидкости из одного резервуара в другой, а могут и быстро, например, при резком перекрытии трубопровода. В первом случае течение называется медленно изменяющимся, во втором – быстро изменяющимся.
Перестройка потока вызывается изменением режима работы гидросистемы за счет внешнего воздействия, либо наличием в самой системе элемента, работающего в циклическом режиме, например, пульсатора (насоса, гидромотора и пр.). И в том и другом случае изменения в параметры потока первоначально вносятся в месте установки элемента, работающего в переменном режиме. Передача этого возмущения всей остальной жидкости осуществляется волнами сжатия и расширения рабочей среды. Это быстро изменяющиеся течения.
|
|
|
Характеристики волн расширения и сжатия зависят от ее упругости, поэтому при анализе волновых процессов пренебрегать сжимаемостью недопустимо. Рассмотрим пример. Пусть имеются два резервуара, соединенные трубопроводом с запорным клапаном, рис. 1.1.
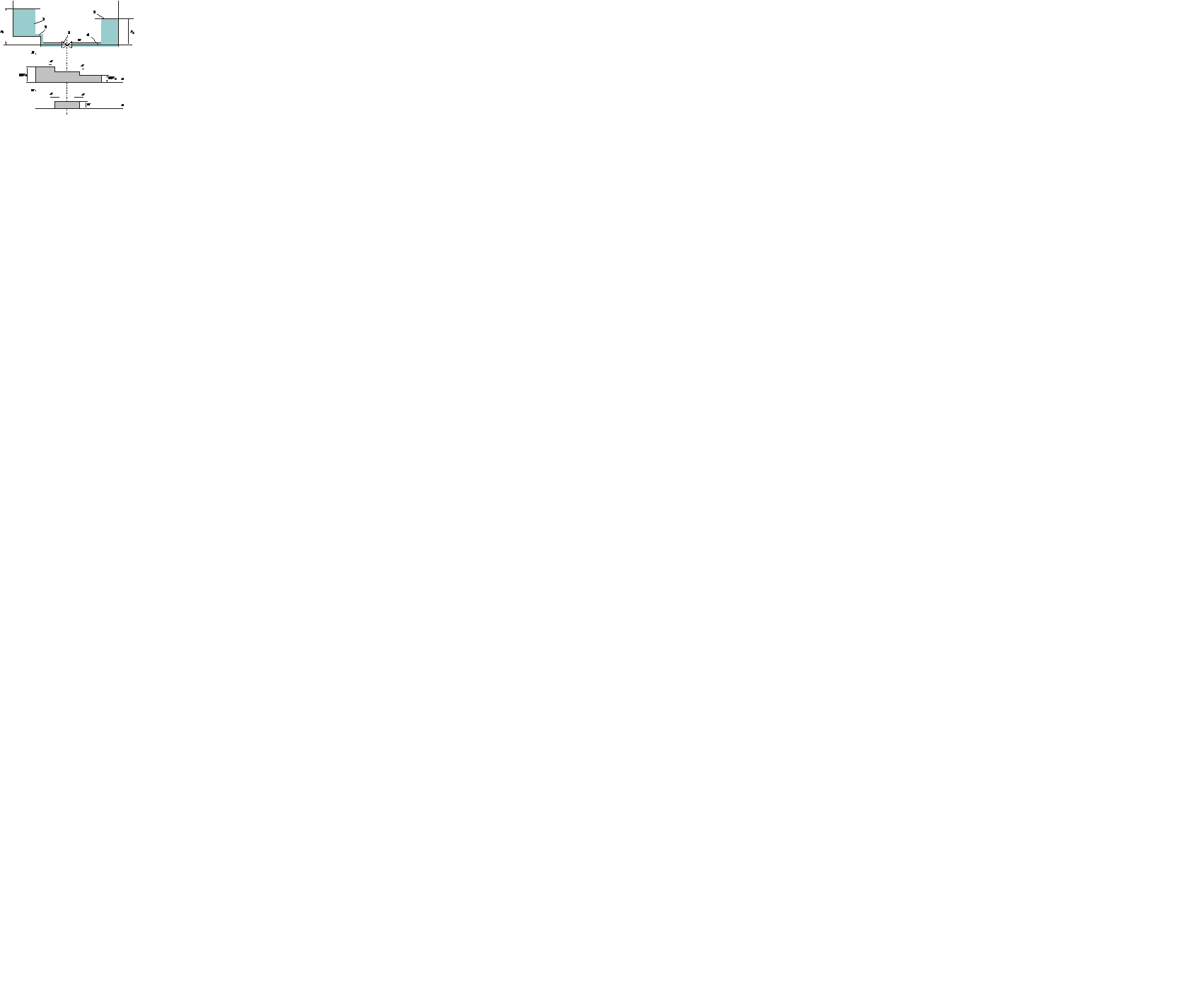
Рис. 1.1. Пример нестационарного течения
Пусть первоначально клапан перекрыт, скорость течения в трубопроводе равна нулю, а давления определяются высотой уровней жидкости в резервуарах: в левом трубопроводе р2 = rgz1; в правом р4 = rgz2. Поскольку уровень в левом резервуаре выше, то жидкость в левом трубопроводе испытывает большее сжатие чем в правом, то есть р2 > р4.
При резком (мгновенном) открытии клапана произойдет расширение более сжатой жидкости, примыкающей к клапану слева и ее переток из левого трубопровода в правый, что будет сопровождаться выравниванием давлений: падением давления в левом трубопроводе и повышением в близлежащих к клапану слоях жидкости в правом трубопроводе. Затем этот процесс будет распространяться на более отдаленные от клапана слои жидкости.
|
|
|
Следовательно, открытие клапана приведет к образованию двух волн, распространяющихся от него в противоположные стороны. Одна волна распространяется по трубопроводу 2 влево и несет с собой понижение давления и увеличение скорости (волна расширения), другая (волна сжатия) распространяется по трубопроводу 4 вправо и приводит к повышению давления и скорости, см. рис. 1.1.
Обе волны, достигнув резервуаров, отразятся от них. Появятся новые (отраженные) волны, которые направятся в сторону клапана и будут нести с собой определенные изменения давления и скорости. Встреча этих волн с клапаном приведет к образованию новых волн и т. д. В гидросистеме возникнет волновой процесс, который постепенно затухая, приведет ее к новому стационарному состоянию.
В сущности, все нестационарные течения представляют собой волновые процессы, ибо только волны передают всему потоку возмущения, вносимые в каком либо месте гидросистемы.
Параметром, характеризующим степень нестационарности течения, является локальное ускорение потока
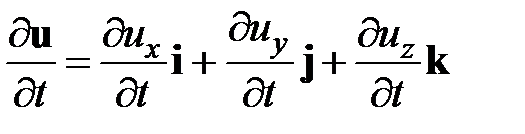 .
.
|
|
|
Локальные ускорения особенно велики у быстро изменяющихся течений, связанные с ними силы способны вызвать сильные волны расширения и сжатия.
У медленно изменяющихся потоков локальные ускорения и интенсивность волн существенно меньше. Поэтому для моделирования таких течений применяют упрощенные математические модели (модели несжимаемой жидкости), исключающие волновой процесс. То есть в таких моделях предполагается, что любое внешнее возмущение передается сразу всей жидкости потока, а не постепенно, слой за слоем, как происходит в действительности.
Как известно из теории подобия, соотношение локальных и конвективных ускорений определяется числом Струхаля
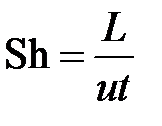 ,
,
где L, u, t – характерные размер области течения, скорость потока и время процесса соответственно.
Число Струхаля растет при увеличении относительной величины локального ускорения потока. Поэтому быстро изменяющимся течениям соответствуют большие числа Струхаля, а медленно изменяющимся – малые.
Скорость распространения волн
Скорость распространения волн сжатия и расширения жидкости в трубах определяется упругими свойствами жидкости и стенок трубопровода. При этом большое значение имеет воздух или газ, содержащийся в жидкости в нерастворенном виде, даже в небольшом количестве.
Рассмотрим участок трубопровода, заполненный жидкостью, ограниченный с одной стороны поршнем, рис. 1.2. Пусть жидкость содержит нерастворенный в ней газ с объемной долей b.
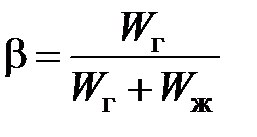 ,
,
где Wг, Wж – объем газа и жидкости соответственно в рассматриваемом участке трубопровода.

Рис. 1.2. К определению скорости волны
Плотность смеси жидкости и газа определится через плотности составляющих следующим образом
 .
.
Пусть в начальный момент времени поршень находится в покое, то есть скорость жидкости равна нулю v = 0. Приложим к поршню силу DF, под действием которой поршень переместится и приведет в движение слои жидкости, располагающиеся вблизи него. Скорость жидкости в этих слоях возрастет на величину Dv, а давление на Dр и данные возмущения распространяются от слоя к слою со скоростью а. За интервал времени d t волна возмущений распространится на величину d х = а×d t, например, от сечения 1 до сечения 2, что приведет к изменению количества движения жидкости, заключенной между этими сечениями. В соответствии с законом сохранения количества движения можем записать
 .
.
Если пренебречь импульсом сил трения 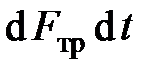 по сравнению с импульсом сил давления
по сравнению с импульсом сил давления 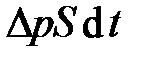 и учесть, что
и учесть, что 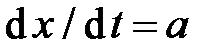 , то получим следующее уравнение, связывающее приращение давления и скорости жидкости в волне
, то получим следующее уравнение, связывающее приращение давления и скорости жидкости в волне
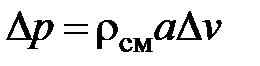 .
.
Считая границы сечений 1 и 2 неподвижными, запишем закон сохранения массы для объема жидкости, заключенной между ними при прохождении волны сжатия
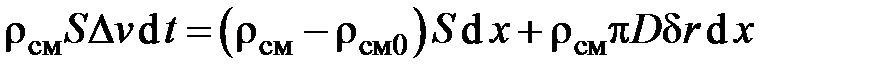 .
.
Здесь rсм0 – плотность невозмущенной жидкости, содержащей нерастворенный газ; D – диаметр трубопровода; dr – приращение радиуса трубопровода за счет повышения давления на величину Dр. Первое слагаемое в правой части представляет собой увеличение массы жидкости за счет изменения плотности, обусловленного сжатием, как газа, так и жидкости, а второе – за счет деформации стенок трубопровода. Разделим обе части на rсмSd x и учтем, что 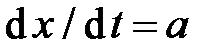
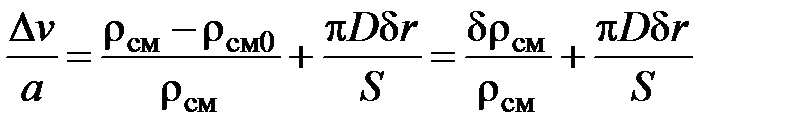 .
.
Преобразуем первый член правой части . Для этого рассмотрим некоторую массу жидкости  , подвергающуюся сжатию давлением d p. Так как при сжатии масса не изменяется, то
, подвергающуюся сжатию давлением d p. Так как при сжатии масса не изменяется, то 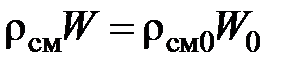 . Из последнего соотношения следует
. Из последнего соотношения следует
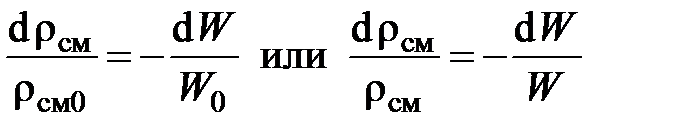 ,
,
где rсм0, W0 – начальное значение плотности и объема рассматриваемой массы жидкости.
Учитывая, что 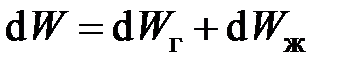 и
и 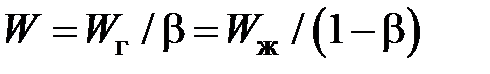 представим в виде
представим в виде
 .
.
Процесс сжатия будем считать адиабатическим, тогда справедливо соотношение 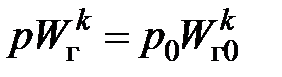 , дифференцируя которое, получим
, дифференцируя которое, получим
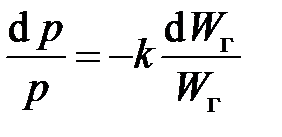 .
.
Для капельной жидкости изменение объема при сжатии связано с изменением давления через модуль упругости (закон Гука для жидкости) Еж:
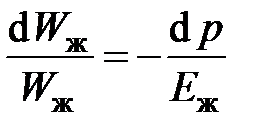 .
.
Подставляя и в , получим
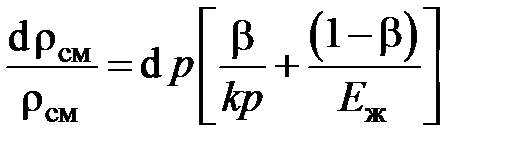 .
.
Ограничимся рассмотрением малых приращений давления в волне сжатия. Тогда первый член правой части уравнения может быть представлен в форме .
Преобразуем теперь последний член . Так как 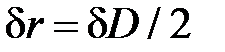 , то
, то
 .
.
В соответствии с законом Гука
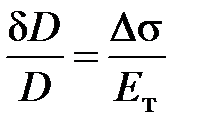 ,
,
где Ds – приращение напряжений материала стенки трубопровода при повышении давления на Dр; Ет – модуль упругости материала трубопровода.
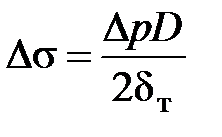 ,
,
где dт – толщина стенки трубопровода.
Подставив и в , получим
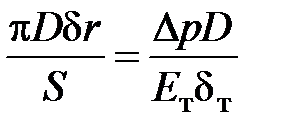 .
.
С учетом , и выражение примет вид
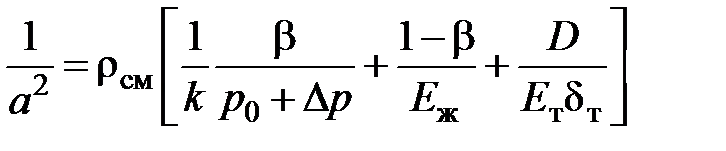 .
.
Соотношение показывает, что скорость распространения волн в газонасыщенной жидкости зависит от величины приращения давления Dр. При этом скорость волн сжатия тем выше, а волн разрежения тем ниже, чем больше величина приращения Dр. Увеличение газосодержания (увеличение b) уменьшает скорость распространения волн.
Скорость распространения слабых волн 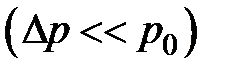 принято называть скоростью звука и обозначать а0. Из следует, что
принято называть скоростью звука и обозначать а0. Из следует, что
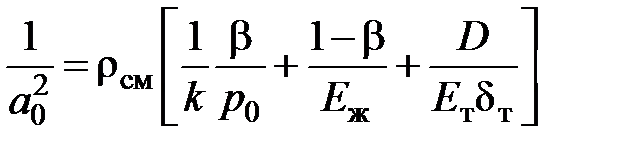 .
.
Выражение
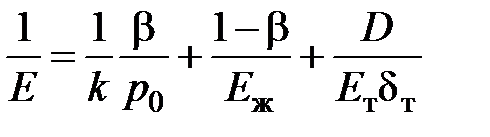 .
.
Представляет собой приведенный модуль упругости слабо газонасыщенной жидкости в нежестком трубопроводе. Отсюда следует выражение
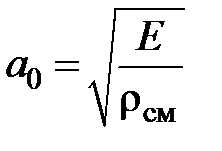 .
.
Если жидкость не содержит газа 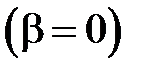 , а стенки трубопровода жесткие
, а стенки трубопровода жесткие 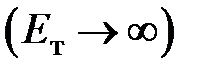 , то Е = Еж и скорость распространения слабых и умеренно сильных волн, несущих изменение давления
, то Е = Еж и скорость распространения слабых и умеренно сильных волн, несущих изменение давления 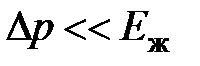
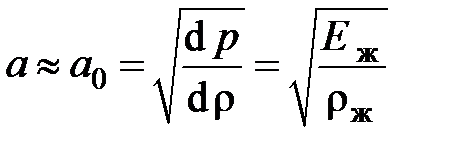 .
.
Например, для воды (r = 10 3 кг/м3, Еж = 2,1×10 9 Па ) а0 = 1450 м/с, а для масла АМГ–10 (r = 850 кг/м3, Еж = 1,35×10 9 Па ) а0 = 1250 м/с.
Упругие стенки трубопровода снижают скорость распространения волн. В этом случае
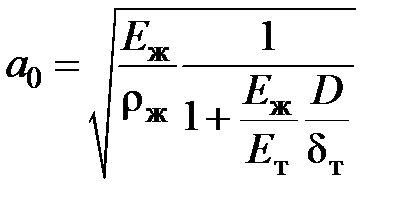 .
.
Например, при относительной толщине трубопровода d/D = 1/20 в стальной трубе (Ет = 2,1×10 11 Па) скорость волны в воде а0 = 1450/1,1 =1320 м/с, а в масле а0 = 1250/1,06 =1190 м/с.
Таким образом, скорость распространения ударных волн и звука в жидкости без нерастворенного газа имеют порядок 103 м/с.
Скорость звука в газе (b = 1, rсм = r0) в жестком трубопроводе (Ет ® ¥) в соответствии с
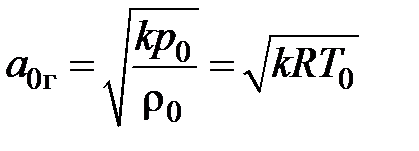 .
.
Например, для воздуха (k = 1,4, R = 287 Дж/кг×К) в диапазоне температур от минус 50 °С до 50 °С
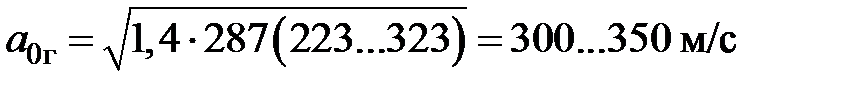 .
.
Интересно отметить, что при низком давлении скорость звука в газожидкостной смеси может быть существенно ниже, чем даже скорость звука в газе, что видно из рис. 1.3, где приведены результаты расчета по формуле скорости звука в воде, содержащей воздух.

Рис. 1.3. Влияние давления и газосодержания на скорость звука
1.3. Дифференциальные уравнения нестационарного движения
жидкости в трубопроводе
Система дифференциальных уравнений, описывающих нестационарное движение сжимаемой вязкой жидкости в трубопроводе, представляет собой уравнение Бернулли и уравнение неразрывности.
Уравнение Бернулли (уравнение движения). Как известно из курса МЖГ, общая форма уравнения Бернулли для произвольной трубки тока с элементом длины 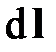 имеет вид
имеет вид
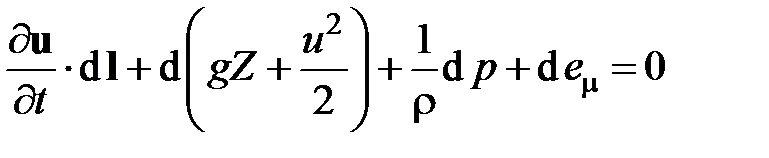 ,
,
где Z – вертикальная координата рассматриваемой точки линии тока; u и u – вектор локальной скорости жидкости в данной точке и его абсолютная величина соответственно; r – плотность жидкости; еm – потери механической энергии потока на преодоление вязких сил сопротивления. Дифференциалы в вычисляются по направлению линии тока 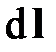 .
.
Получим, используя , уравнение Бернулли для осредненных по поперечному сечению трубопровода параметров. Для этого проинтегрируем уравнение по площади поперечного сечения.
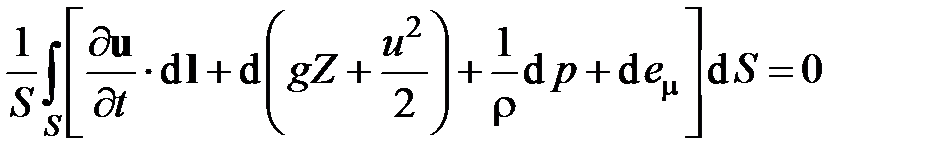 .
.
Рассматривать будем плавноизменяющиеся течения, для которых поперечные составляющие скорости, а также углы, образующиеся между соседними линиями тока, малы. Для таких течений давление р и плотность r можно считать постоянными в пределах рассматриваемого сечения трубопровода. Интегрирование будем выполнять в системе координат, связанной с осью трубопровода: ось х направлена по оси трубопровода, оси y и z ортогональны ей. Рассмотрим более подробно подынтегральную функцию. Так как векторы u и l коллинеарны, то
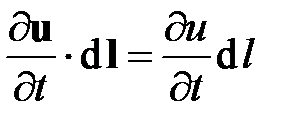 .
.
Дифференциалы вдоль линии тока представляют собой выражения вида
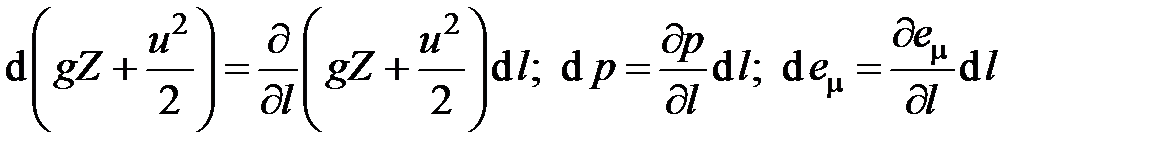 .
.
Подставив эти формулы в и сокращая на 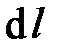 , получим
, получим

Производные по направлению l выражаются формулами типа
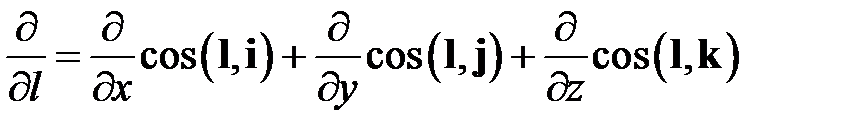 .
.
Учитывая допущение о рассмотрении только плавноизменяющихся течений, направляющие косинусы между направлением l и осями y и z можно считать равными нулю. Тогда примет вид
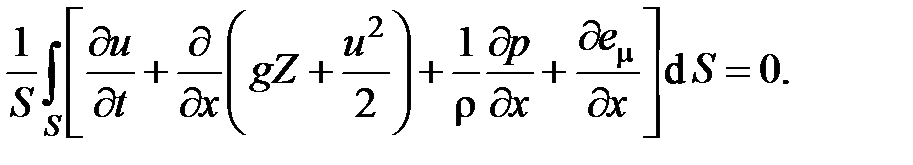
Выполним интегрирование в . Рассмотрим первое слагаемое
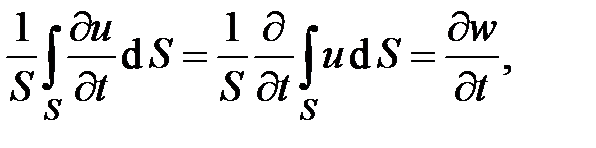
где w – средняя по поперечному сечению скорость потока 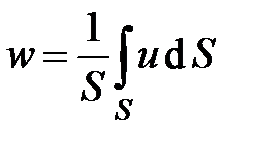 .
.
Второе слагаемое преобразуется следующим образом
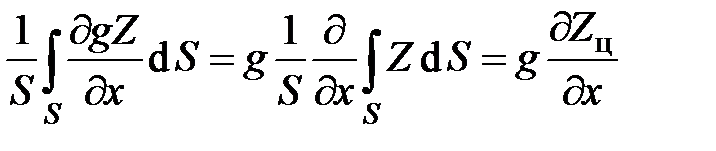 ,
,
где Zц – вертикальная координата центра масс рассматриваемого сечения 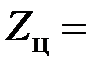
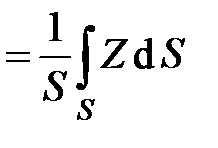 .
.
Интегрирование третьего слагаемого дает
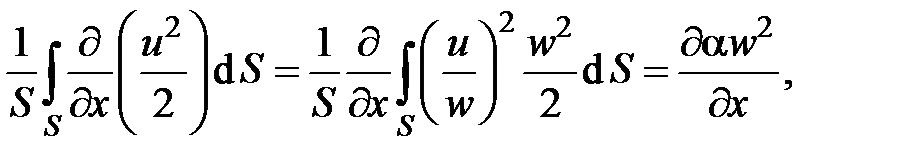
где a – коэффициент осреднения (коэффициент количества движения или коэффициент Буссинеска) имеющий следующий вид
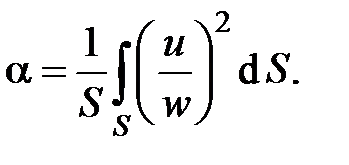
Так как давление и плотность постоянны по площади сечения, то четвертое слагаемое остается без изменений.
Потери удельной (отнесенной к единице массы движущегося потока) энергии еm представляют собой затраты энергии на преодоление сил трения. Исходя из этого, и соображений размерности можем записать
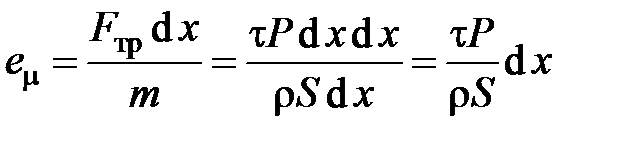 ,
,
где Fтр – сила трения; m – масса жидкости в участке трубопровода длиной d x; Р – периметр трубопровода; t – напряжения трения, действующие на стенках трубопровода.
Таким образом, после осреднения уравнение Бернулли для нестационарного движения сжимаемой жидкости в трубопроводе принимает вид
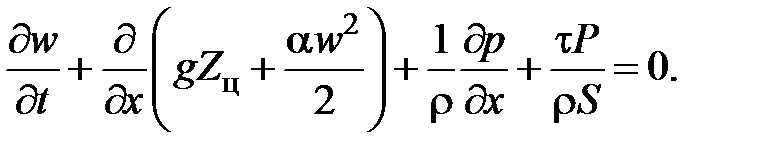
Уравнение можно еще упростить, если учесть, что сжимаемость реальных жидкостей, характеризуемая модулем упругости 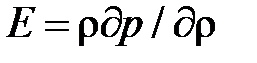 , как правило, незначительна. По крайней мере, в большинстве случаев справедливо соотношение
, как правило, незначительна. По крайней мере, в большинстве случаев справедливо соотношение 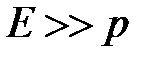 . Тогда имеем
. Тогда имеем
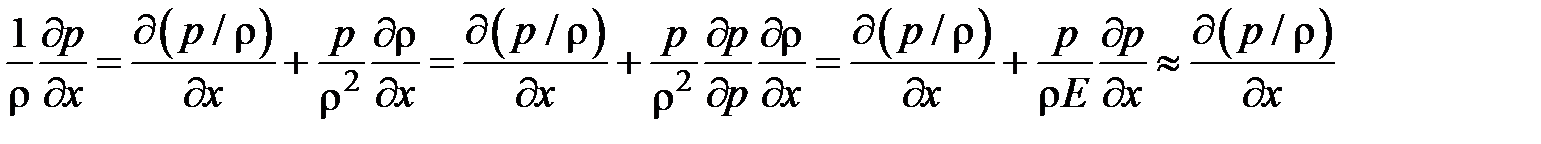 .
.
С учетом последнего соотношения уравнение принимает вид
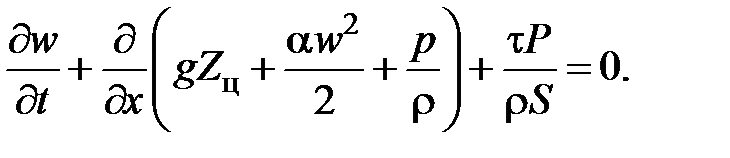
Или, переходя к напорам,
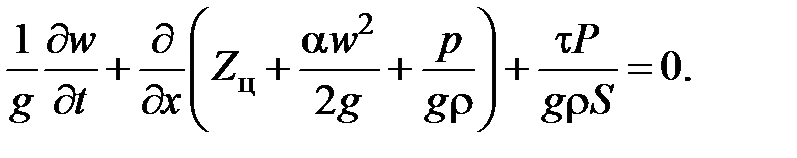
Выражение в скобках представляет собой полный напор потока
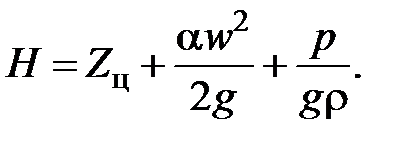
Уравнение неразрывности. Уравнение неразрывности для нестационарного движения сжимаемой жидкости в трубопроводе получим так же, как уравнение Бернулли, проинтегрировав общее уравнение неразрывности МЖГ
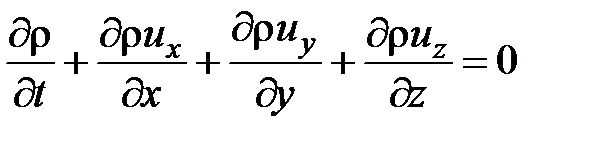
по площади поперечного сечения трубопровода S. Рассматривая плавноизменяющиеся течения, получим
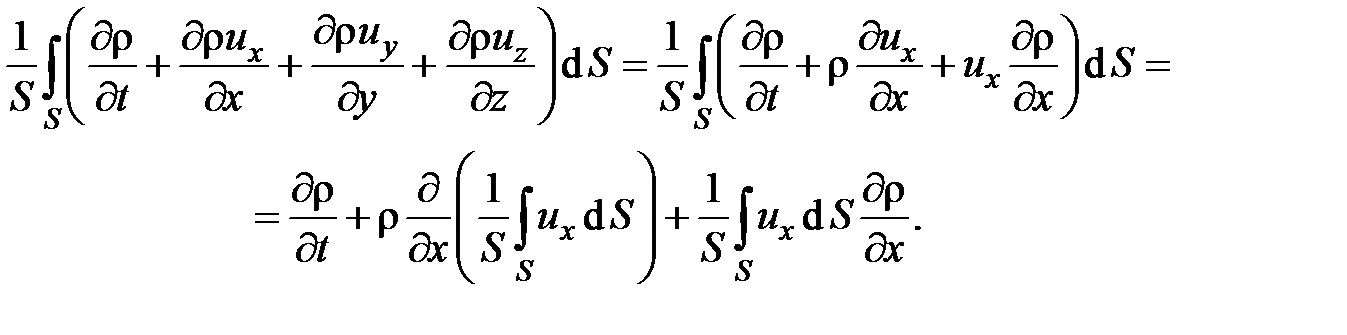
Таким образом, уравнение неразрывности для рассматриваемого случая течения имеет вид
 .
.
Учитывая, что 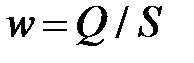 , где Q – объемный расход, последнее уравнение можно представить и следующим образом
, где Q – объемный расход, последнее уравнение можно представить и следующим образом
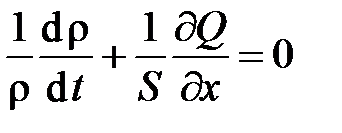 .
.
Получим еще одну форму уравнения неразрывности, необходимую для анализа волнового движения жидкости, используя определение модуля упругости жидкости Е. Преобразуем следующим образом производную от плотности в последнем уравнении
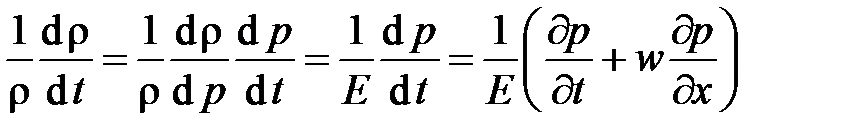
С учетом уравнение запишется
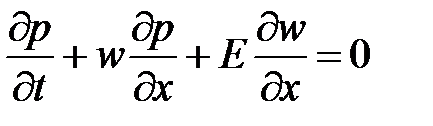 .
.
Учитывая, что 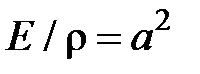 , последнее уравнение примет вид
, последнее уравнение примет вид
 .
.
1.4. Волновые уравнения для потока жидкости в
длинных трубопроводах
Волны сжатия и расширения, причиной появления которых при внесении возмущений в поток жидкости является сжимаемость среды, передают изменения параметров потока (скорости и давления) из одного узла гидросистемы в другой. Найдем закономерности распространения этих волн.
Идеальная жидкость. Рассмотрим течение идеальной сжимаемой жидкости в длинном горизонтальном трубопроводе с постоянной площадью поперечного сечения. Для идеальной жидкости t = 0. Уравнение Бернулли для этого случая имеет вид
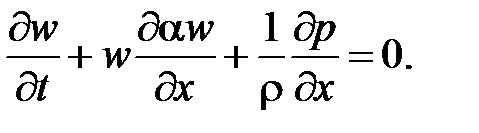
Сравним порядки членов уравнения , содержащих конвективные производные. Считая, что течение происходит со скоростями существенно меньшими скорости распространения волн (w << a) и, используя , можем записать
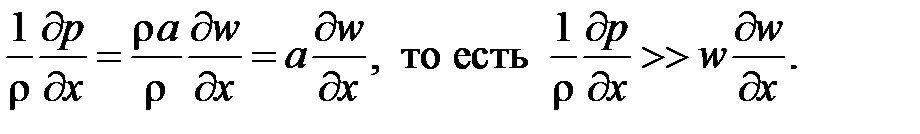
Аналогичные оценки выполним и для уравнения неразрывности
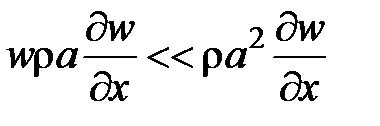 .
.
Тогда, с учетом полученных оценок, уравнение Бернулли и уравнение неразрывности для рассматриваемого случая течения примут вид
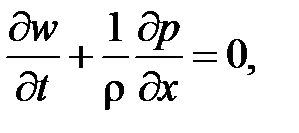
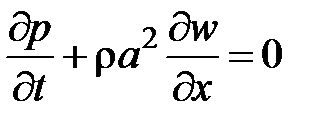 .
.
Найдем решение системы уравнений , . Для этого умножим первое из них на rа и сложим со вторым:

Будем считать, что плотность жидкости и скорость волны изменяется незначительно. Это справедливо, при умеренных колебаниях давления и незначительной объемной доли нерастворенного газа в рабочей жидкости. Тогда произведение rа можно внести под знак производной.
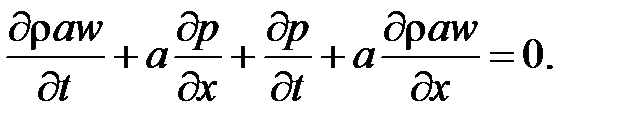
После преобразований уравнение принимает вид
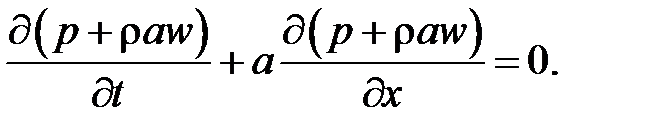
Вычтя умноженное на rа уравнение из уравнения и повторив выполненные выше преобразования, получим
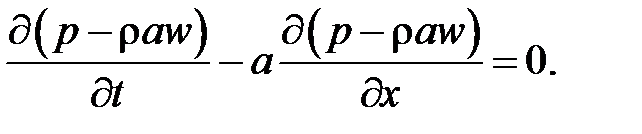
Полученные уравнения и представляют собой систему линейных дифференциальных уравнений в частных производных первого порядка с постоянными коэффициентами. Их общее решение выражается через произвольные, но дифференцируемые функции координаты и времени:
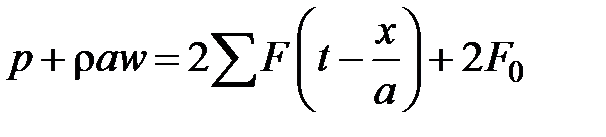 ;
;
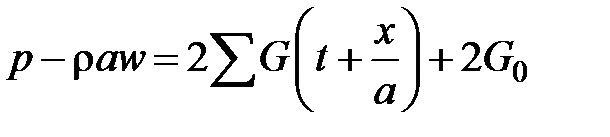 ,
,
где F0, G0 – константы, которые определяются начальными параметрами потока (р0, w0):
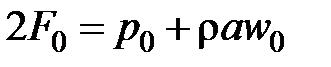 ;
;
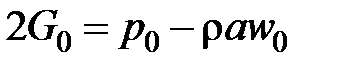 .
.
Функции F и G (так называемые волновые функции) определяются внешними возмущениями, вносимыми в поток, а также взаимодействием потока с различными элементами гидросистемы. Если возмущений нет, то F = G = 0. Коэффициент 2, присутствующий в выражениях , введен для упрощения вида конечного результата решения.
Убедиться, что является решением уравнения , а – уравнения можно непосредственной подстановкой, что превращает исходные уравнения в тождества.
С учетом и решение системы , принимает вид
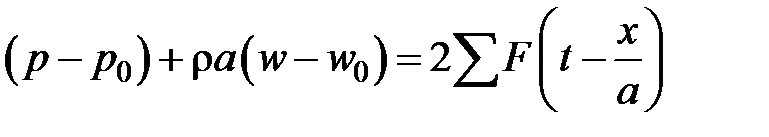 ;
;
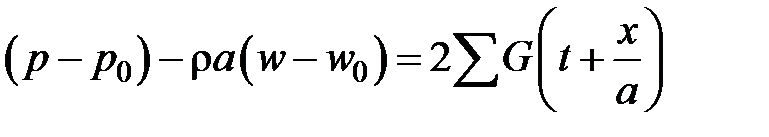 .
.
Сложение и вычитание уравнений и приводит решение к виду, которое в явной форме выражает изменение давления и скорости течения идеальной сжимаемой жидкости через волновые функции:

Рассмотрим подробнее смысл волновых функций 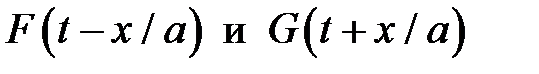 . Пусть состояние потока в сечении 1 с координатой х1 в момент времени t1 описывается функциями
. Пусть состояние потока в сечении 1 с координатой х1 в момент времени t1 описывается функциями 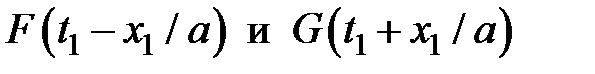 . Так как одинаковым значениям аргумента соответствуют одинаковые значения функций, то изменение состояния потока, наблюдающееся в сечении х1 в момент времени t1, повторится позже (при t2 > t1) в другом сечении 2 с координатой х2, такой, что:
. Так как одинаковым значениям аргумента соответствуют одинаковые значения функций, то изменение состояния потока, наблюдающееся в сечении х1 в момент времени t1, повторится позже (при t2 > t1) в другом сечении 2 с координатой х2, такой, что:
· для функции  должно выполняться равенство
должно выполняться равенство 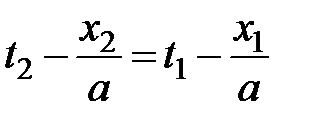 и, следовательно
и, следовательно 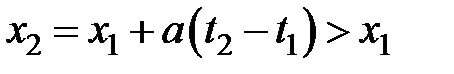 ;
;
· для функции 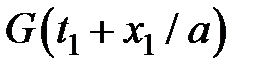 должно выполняться равенство
должно выполняться равенство 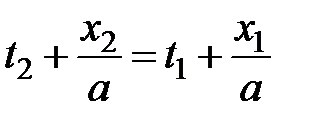 и, следовательно
и, следовательно 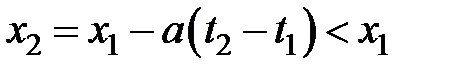 .
.
Следовательно, изменение состояния потока, описываемое функцией F будет повторяться с некоторым запозданием в сечении х > х1, а возмущения, описываемые функцией G, с опозданием повторится в сечениях с х < х1.
Таким образом, функция 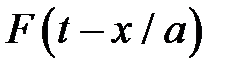 описывает волны, бегущие вдоль оси х, а уравнение – распространение этих волн в потоке жидкости и изменение параметров течения по пути следования этих волн.
описывает волны, бегущие вдоль оси х, а уравнение – распространение этих волн в потоке жидкости и изменение параметров течения по пути следования этих волн.
Другая функция 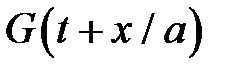 и уравнение описывает волны, бегущие против оси х (против потока) и их влияние на параметры течения.
и уравнение описывает волны, бегущие против оси х (против потока) и их влияние на параметры течения.
В начальной стадии волнового процесса, когда присутствуют только две волны, распространяющиеся от источника возмущения, и нет волн отраженных от соседних узлов гидросистемы, изменение давления и скорости потока выражаются только через волновые функции F и G только этих двух волн:
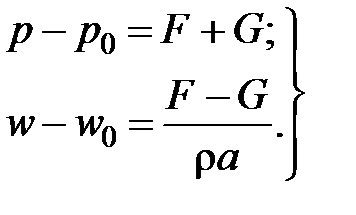
Как видно из для анализа волновых процессов можно использовать принцип суперпозиции, в соответствии с которым изменение давления и скорости в любой точке потока в любой момент времени определяется путем суммирования соответствующих изменений от каждой волны. Также путем суммирования изменений от каждой волны определяются и параметры течения.
Реальная жидкость. При описании динамики реальной жидкости в уравнении движения сохраняется член с напряжением трения t, а само уравнение имеет вид
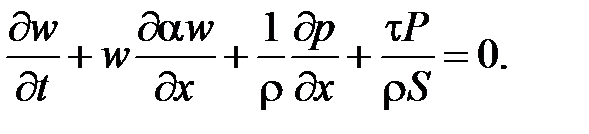
Это уравнение, совместно с уравнением неразрывности образуют систему дифференциальных уравнений в частных производных гиперболического типа. Она может быть решена методом характеристик. Характеристические уравнения бегущих волн для этой системы имеют вид:
· для характеристики 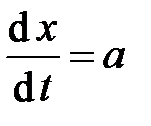 или
или 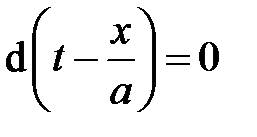 , то есть в фазовой плоскости волны F, распространяющейся вдоль оси х, направленной по потоку
, то есть в фазовой плоскости волны F, распространяющейся вдоль оси х, направленной по потоку
 ;
;
· для характеристики 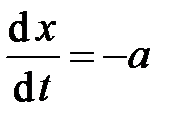 или
или 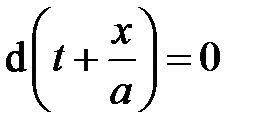 , то есть в фазовой плоскости волны G, распространяющейся против оси х, направленной по потоку
, то есть в фазовой плоскости волны G, распространяющейся против оси х, направленной по потоку
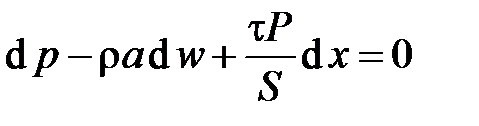 .
.
Перейдем в уравнениях , от давления к напорам  , а от скорости – к объемному расходу
, а от скорости – к объемному расходу 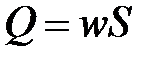 и введем безразмерные переменные:
и введем безразмерные переменные:
· относительный напор 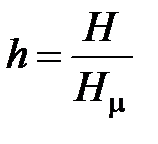 ;
;
· относительный расход 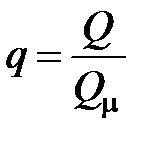 ;
;
· относительные касательные напряжения 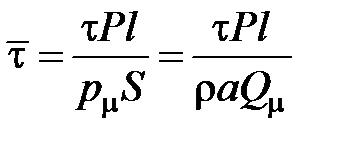 ;
;
· относительную продольную координату 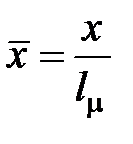 ;
;
· относительное время 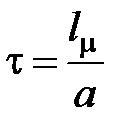 .
.
При назначении масштабных величин 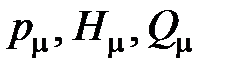 потребуем выполнения равенств
потребуем выполнения равенств 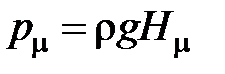 ,
, 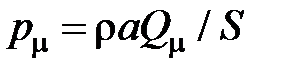 . В качестве масштаба длины lm примем длину расчетного участка гидролинии (между соседними узлами) lm = l.
. В качестве масштаба длины lm примем длину расчетного участка гидролинии (между соседними узлами) lm = l.
В результате получим
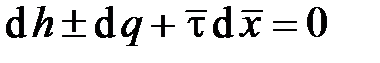 ,
,
Знак «плюс» в относится к волне F, «минус» – к волне G.
Уравнения характеристических направлений в относительных переменных примут вид
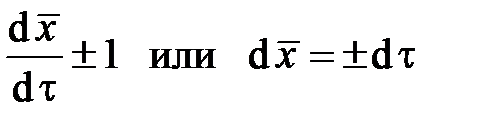 .
.
Касательные напряжения t выражаются через коэффициент трения l:
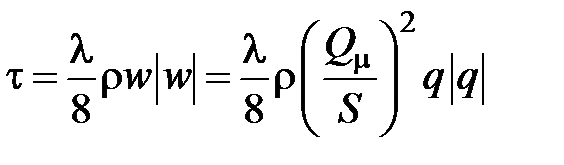 ,
,
тогда
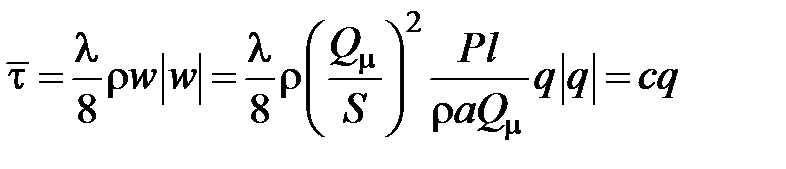 ,
,
где с – параметр сопротивления гидролинии
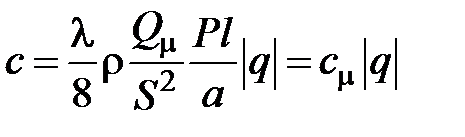 ,
,
а для круглого трубопровода диаметром D
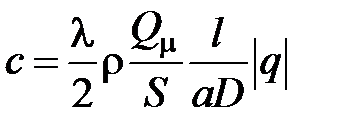 .
.
Средняя величина относительного касательного напряжения 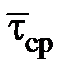 на расчетном участке трубопровода между двумя узлами гидролинии: начальным по ходу волны «н» и конечным «к» (
на расчетном участке трубопровода между двумя узлами гидролинии: начальным по ходу волны «н» и конечным «к» ( 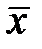 = 0…1) может быть приближенно определена по формуле
= 0…1) может быть приближенно определена по формуле
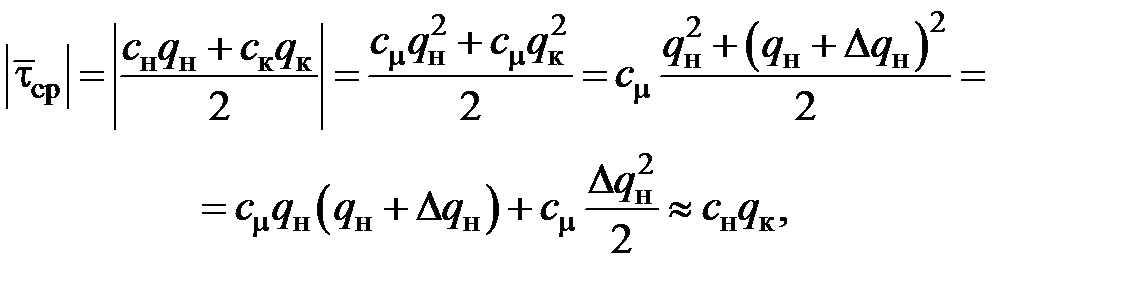
то есть может быть приближенно вычислена путем умножения параметра сопротивления трения сн в начальном по ходу волны узле на относительный расход qк в конечном (противоположном) узле.
Используя формулу , получим выражения для интеграла уравнений в фазовых плоскостях волн (вдоль характеристических направлений) в конечно-разностном виде.
Пусть k + 1 и k – два узла на гидролинии, имеющие координаты 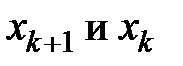 , причем
, причем 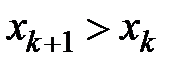 . Относительное время пробега волн между узлами
. Относительное время пробега волн между узлами
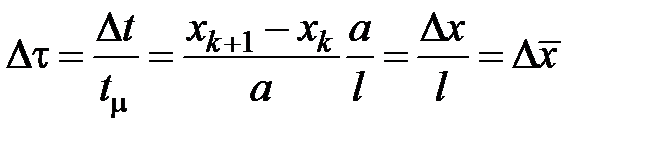 .
.
Обозначим начальный момент временного интервала интегрирования tн = i, тогда конечный момент tк = tн + Dt = i + 1. Заменим дифференциалы в уравнении конечными разностями, учитывая физический смысл волновых уравнений: волна F переносит информацию о параметрах потока по ходу течения жидкости, а волна G – против хода течения. Тогда, например, первый дифференциал в для волны F мы должны представить как разность напора в узле с координатой xk + 1 в момент времени i + 1 и напора в узле с координатой xk в момент времени i, то есть 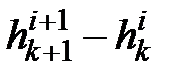 . Для волны G аналогичный дифференциал должен быть аппроксимирован, как
. Для волны G аналогичный дифференциал должен быть аппроксимирован, как 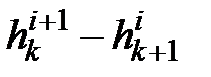 . Кроме того для волны F, в соответствии с и ,
. Кроме того для волны F, в соответствии с и , 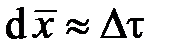 , для волны G
, для волны G 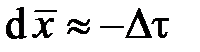 .
.
С учетом этих замечаний интегралы характеристических уравнений в конечно-разностной форме можно выразить следующим образом:
· для волн F, бегущих вдоль оси х*

или
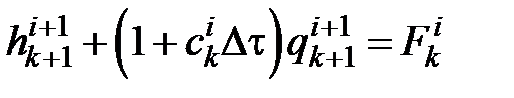 ,
,
где 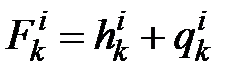 – волновая функция;
– волновая функция;
· для волн G, бегущих против оси х
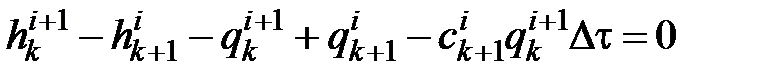
или
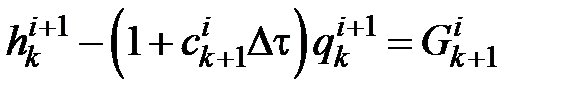 ,
,
где 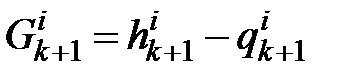 – волновая функция.
– волновая функция.
В частном случае, когда расстояние меду соседними узлами 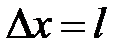
 и уравнения и упрощаются
и уравнения и упрощаются
 ,
,
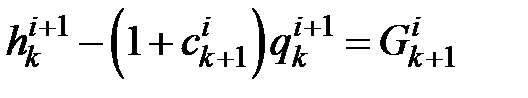 .
.
Дата добавления: 2018-11-24; просмотров: 278; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
