Аппроксимация частотных характеристик

Фильтра нижних частот - прототипа

Анализ требований к частотным характеристикам фильтра

Синтез полосового фильтра существенно упрощается, если его частотные характеристики удовлетворяет условиям геометрической симметрии.

Для симметричных частотных характеристик полосового фильтра выполняется условие:

f_c₁×f_c₂ = f_s₁×f_s₂. (2)

Если условие геометрической симметрии не выполняется, то проводится коррекция одной из частот f_s₁ или f_s_{2 .}

Для этого рассчитываются новые значение частот среза полосы задерживания , (3)

В качестве скорректированного значения частоты среза выбирают то значение, которое ужесточит заданные требования к частотным характеристикам, т.е. приведет к уменьшения ширины одной из двух полос расфильтровки. Если

f_s₁₁>f_s₁, то новое значение частоты среза полосы задерживания f_s_11,в противном случае - f_s₂₂.

Нормирование фильтра частотных характеристик

Нормирование частотной характеристики позволяет перейти к упрощенному расчету частотной характеристики ослабления ФНЧ - прототипа.

Безразмерные нормированные частоты ЧХЗ ФНЧ - прототипа равны:

W_c = 1; 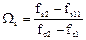, если f_s₁₁>f_s₁или 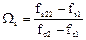, если f_s₂₂<f_s₂. (3)

Тогда график допусков для частотной характеристики ослабления ФНЧ-прототипа примет вид:

Рисунок 3 - График допусков частотной характеристики ослабления ФНЧ - прототипа

Аппроксимация частотной характеристики ФНЧ-прототипа

Аппроксимация частотных характеристик ФНЧ-прототипа состоит в определении "нулей" и "полюсов" заведомо реализуемой функции, которой заменяют (аппроксимируют) частотную характеристику ослабления или АЧХ ФНЧ-прототипа.

Наибольшее применение при синтезе электрических фильтров нашли следующие четыре вида аппроксимации:

- по Батерворту (рисунок 4а)

- по Чебышеву полиномиальная (рисунок 4б),

- по Чебышеву инверсная (рисунок 4в),

- по Золотареву-Кауэру (рисунок 4г).

Рисунок 4 - График частотных характеристик ослабления ФНЧ - прототипа при различных видах аппроксимации

Для этих видов аппроксимации обычно используют формулы, полученные для "нулей" и "полюсов" нормированной передаточной функции ФНЧ-прототипа, представленной в виде:

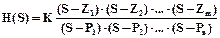, (4)

где К - нормирующий коэффициент;

S =s+ jW - нормированная комплексная частота;

Z_i = s_zi + jW_zi, i = 1,m - "нули" передаточной функции Н(S);

P_i = s_pi + jW_pi, i = 1,n - "полюсы" передаточной функции H(S).

Знаменатель физически реализуемой функции (4) является полиномом Гурвица порядка n, т.е. все n "полюсов" функции (4) должны лежать в левой полуплоскости комплексной плоскости: s_pi < 0, i = 1,n.

Порядок полинома Гурвица определяет порядок ФНЧ-прототипа.

Положение "нулей" функции (4) не ограничивается. Для используемых видов аппроксимации "нули" находятся либо в бесконечности (по Баттерворту и по Чебышеву полиномиальной), либо на мнимой оси (по Чебышеву инверсной и по Золотареву-Кауэру).

Формулы для расчета n, "нулей" и "полюсов" функции H(S):

а) при аппроксимации по Батерворту:

- порядок фильтра определяется как ближайшее большее целое число из соотношения 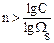, (5)

где ; (6)

W_s определяется согласно (3);

- полюсы , (7)

- нули: Z_i ® ¥, i = 1,m; (8)

б) при аппроксимации по Чебышеву полиномиальной:

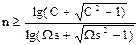, (9)

где С определяется согласно (6), а W_s согласно (3);

«нули»: Z_i ® ¥, i = 1,m;

«полюсы»: (10)

где . (11)

в) при аппроксимации по Чебышеву инверсной:

n определяется согласно (9);

«нули»: 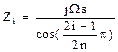, i = 1, 2,..., n; (12)

«полюсы»: 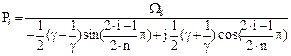(13)

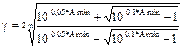где (14)

г) при аппроксимации по Золотареву-Кауэру:

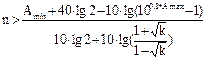, (15)

где .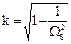

«нули» при n нечетном:

;

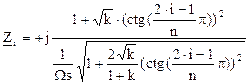Z_n ® ¥

«нули» при n четном:

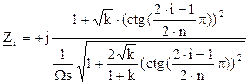
(16)

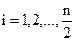
«полюсы»: ,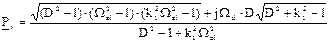

(17)

где ; ξ определяется согласно (11). (18)

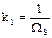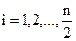; при четном n, 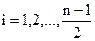при нечетном n.

При нечетном n дополнительный полюс определяется выражением:

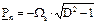. (19)

Для удобства каждая пара сомножителей в (4) с комплексно-сопряженными «полюсами» представляется полиномом второго порядка:

(S - P_i)×(S - P_i_с) = (S - σ_pi - jW_pi)×(S - σ_pi + jW_pi) = S² - 2σ_pi×S + σ_pi² + W_pi² =

= S² + (-2σ_pi)×S + W_oi², (20)

где W_oi² = σ_pi² +W_pi² – собственная частота i-го полюса.

Число полиномов 2-го порядка вида (20) в знаменателе нормированной передаточной функции (4) определяет число звеньев 2-го порядка, необходимых для ее каскадной реализации. При нечетном порядке n знаменателя нормированной передаточной функции ФНЧ-прототипа в число сомножителей функции Н(S) добавляется передаточная функция Н_b(S) звена первого порядка (билина), т.е. получим:

H(S) = K×H₁(S)×H₂(S)×...×H_n/2 (S); - при четном n:

(21)

H(S) = K×H₁(S)×H₂(S)×...×H_(n-1)/2 (S)×H_b(S); - при нечетном n:

где H_i(S) = 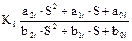, - передаточная функция i-го звена; (22)

K = K₁×K₂×..×K_N, - общий нормирующий коэффициент функции H(S).

N – общее число звеньев, реализующих полученную нормированную передаточную функцию ФНЧ-прототипа H(S).

Нормирующий коэффициент К функции (4) определяется после построения графика нормированной частотной характеристики A(W) и определения по нему величины наименьшего ослабления A_{min min}, которое необходимо свести до нулевого уровня с помощью нормирующего коэффициента К, т.е. из выражения A_min _min = -20×lgK получим: K = 10^0,05^×^Amin^min. (23)

Для проверки правильности расчетов выбранной каскадной реализации ФНЧ-прототипа необходимо построить график нормированной частотной характеристики А(W) и сравнить его с графиком допусков частотной характеристики ФНЧ-прототипа.

Поскольку A(W) = - 20×lgH(W), то после логарифмирования (21) при К = 1 получим: A(W) = A₁(W) + A₂(W) +...+ A_N(W),

где A_i(W) определяется из (22) при S = jW c учетом (1) для интервала частот от W = 0 до W = 2W_z, чтобы проверить все экстремумы функции A(W).

Дата добавления: 2018-11-24; просмотров: 401; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 Следующая ⇒

Мы поможем в написании ваших работ!