Закон распределения вероятностей дискретной случайной величины

Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически.

Каждое значение дискретной случайной величины имеет определенную вероятность появления. Пусть возможное значение x₁ наступает с вероятностью p₁, значение x₂ – с вероятностью p₂ и т.д.

Законом распределениявероятностей дискретной случайной величины X называется любое правило, позволяющее находить все вероятности вида .

Простейшей формой задания закона распределения дискретной случайной величины Х является таблица, которая состоит из двух строк. В первой строке записываются все возможные значения случайной величины, а во второй – вероятности появления этих значений:

X			…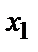
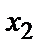
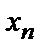
P			…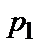

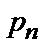
Здесь .

Закон распределения дискретной случайной величины можно изобразить графически. В прямоугольной системе координат строят точки M₁(x₁, p₁), M₂(x₂, p₂), ..., M_n(x_n, p_n) (x_i – возможные значения случайной величины X, p_i – соответствующие вероятности) и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения (рис. 1) или полигоном распределения вероятностей.

 

Рис. 10.1 Многоугольник распределения вероятностей

 

Многоугольник распределения, так же как и ряд распределения, полностью характеризует случайную величину.

Числовые характеристики дискретной случайной величины

Если дискретная случайная величина X задана законом распределения вероятностей вида:

 

X			…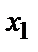
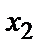
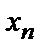
P			…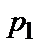

 

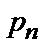
то математическое ожидание  величины  вычисляется по формуле:

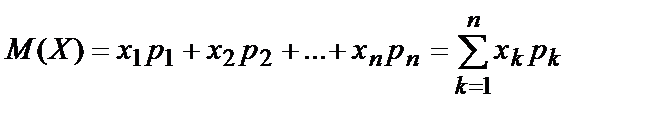.      (10.21)

Математическое ожидание  величины служит характеристикой среднего значения случайной величины .

Математическое ожидание обладает следующими свойствами:

1⁰. Математическое ожидание постоянной величины равно самой постоянной:

М(С)=С,где С=соnst.

2⁰. Постоянный множитель можно выносить за знак математического ожидания:

М(СХ)=С∙М(Х)(С = соnst).

3⁰. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:

М(Х+Y)=М(Х) +М(Y).

Это равенство распространяется на п случайных величин:

М(Х₁+Х₂+…+Х_п)=М(Х₁)+М(Х₂)+…+М(Х_п).

4⁰. Математическое ожидание разности двух случайных величин равно разности их математических ожиданий:

М(Х–Y)=М(Х)–М(Y).

5⁰. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин:

М(Х∙Y)=М(Х)∙М(Y).

Это равенство распространяется на п независимых случайных величин:

М(Х₁∙Х₂∙…∙Х_п)=М(Х₁)∙М(Х₂)∙…∙М(Х_п).

Дисперсиейдискретнойслучайной величины  называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

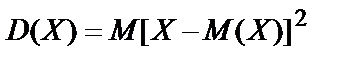 или 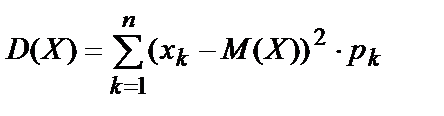. (10.22)

Дисперсию удобно вычислять по формулам:

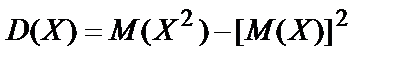 или .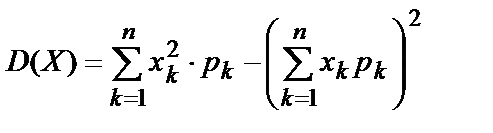

Дисперсия обладает следующими свойствами:

1⁰. Дисперсия постоянной величины равна нулю:

D(С)=0.

2⁰. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:

D(СХ)=С²D(Х)(С=соnst).

3⁰. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий слагаемых:

D(Х+Y)=D(Х)+D(Y).

Это равенство распространяется на п случайных величин:

D(Х₁+Х₂+…+Х_п)=D(Х₁)+D(Х₂)+…+D(Х_п).

4⁰. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:

D(Х–Y)=D(Х)+D(Y).

Средним квадратическим отклонением случайной величины 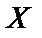называют квадратный корень из дисперсии:

.                                    (10.23)

Дисперсия и среднее квадратическое отклонение характеризуют рассеяние возможных значений случайной величины вокруг её математического ожидания.

---

Дата добавления: 2018-05-12; просмотров: 288; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!