Функция нескольких переменных. Основные понятия
Пусть даны два непустых множества D и U. Если каждой паре действительных чисел (x; y), принадлежащей множеству D, по определенному правилу ставится в соответствии один и только один элемент u из U, то говорят, что на множестве D задана функция f (или отображение) со множеством значений U. При этом пишут 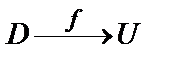 , или
, или 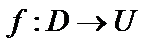 , или
, или 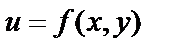 . Множество D называется областью определения функции, а множество U, состоящее из всех чисел вида
. Множество D называется областью определения функции, а множество U, состоящее из всех чисел вида 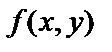 , где
, где 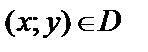 ,
, 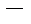 множеством значений функции. Значение функции
множеством значений функции. Значение функции 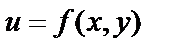 в точке
в точке 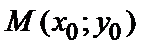 называется частным значением функции и обозначается
называется частным значением функции и обозначается 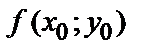 или
или 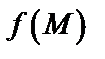 .
.
Частные производные первого порядка
Частной производной от функции 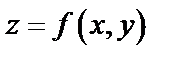 по независимой переменной
по независимой переменной 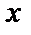 называется конечный предел
называется конечный предел
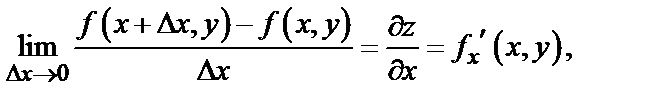
вычисленный при постоянном 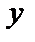 .
.
Частной производной по 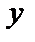 называется конечный предел
называется конечный предел
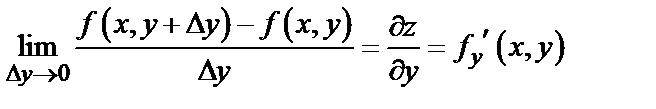 ,
,
вычисленный при постоянном 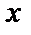 .
.
Для частных производных справедливы обычные правила и формулы дифференцирования.
Полный дифференциал
Полным приращением функции 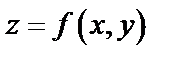 в точке
в точке 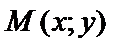 называется разность
называется разность 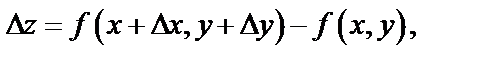 где
где 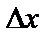 и
и 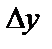
 произвольные приращения аргументов.
произвольные приращения аргументов.
Функция 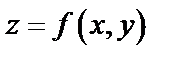 называется дифференцируемой в точке
называется дифференцируемой в точке 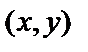 , если в этой точке полное приращение можно представить в виде
, если в этой точке полное приращение можно представить в виде
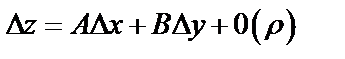 , где
, где 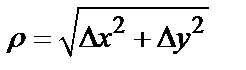 .
.
Полным дифференциалом функции 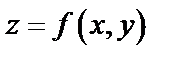 называется главная часть полного приращения
называется главная часть полного приращения 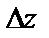 , линейная относительно приращений аргументов
, линейная относительно приращений аргументов 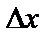 и
и 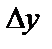 , т.е.
, т.е. 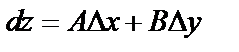 .
.
Дифференциалы независимых переменных совпадают с их приращениями, т.е. 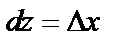 и
и 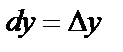 .
.
Полный дифференциал функции 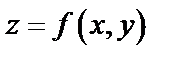 вычисляется по формуле
вычисляется по формуле
|
|
|
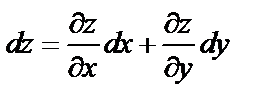 .
.
Аналогично, полный дифференциал функции трех аргументов 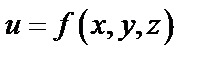 вычисляется по формуле
вычисляется по формуле
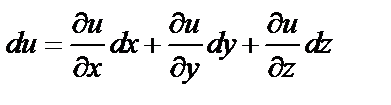 .
.
При достаточно малом 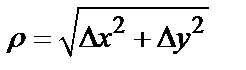 для дифференцируемой функции
для дифференцируемой функции 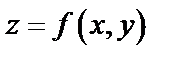 справедливы приближенные равенства
справедливы приближенные равенства
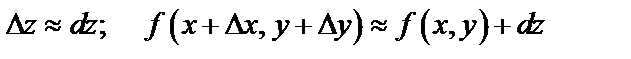 .
.
или
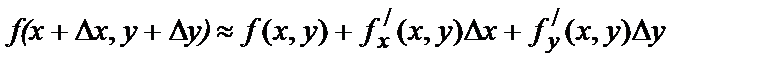 . (7.1)
. (7.1)
Частные производные и дифференциалы высших порядков
Частными производными второго порядка от функции 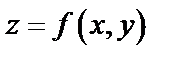 называются частные производные от ее частных производных первого порядка .
называются частные производные от ее частных производных первого порядка .
Обозначение частных производных второго порядка:
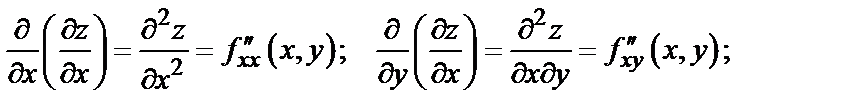
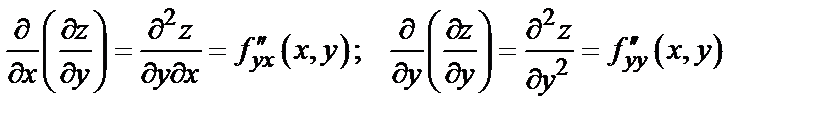 .
.
Аналогично определяются и обозначаются частные производные третьих и высших порядков, например:
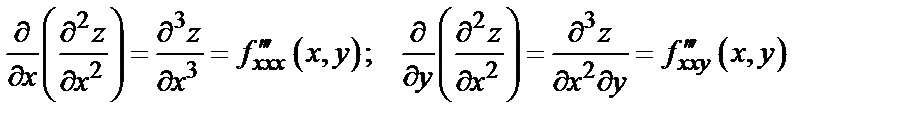 и т.д.
и т.д.
Так называемые «смешанные» производные, отличающиеся друг от друга лишь последовательностью дифференцирования, равны между собой, если они непрерывны, например:
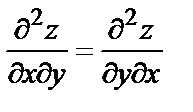 .
.
Дифференциалом второго порядка от функции 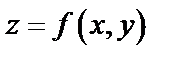 называется дифференциал от ее полного дифференциала, т.е.
называется дифференциал от ее полного дифференциала, т.е. 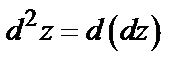 .
.
Аналогично определяются дифференциалы третьего и высших порядков: 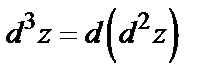 ; вообще
; вообще 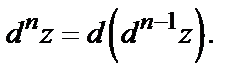
Если x и y – независимые переменные и функция 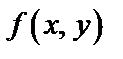 имеет непрерывные частные производные, то дифференциалы высших порядков вычисляются по формулам:
имеет непрерывные частные производные, то дифференциалы высших порядков вычисляются по формулам:
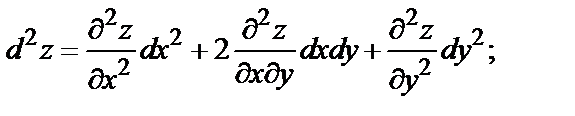
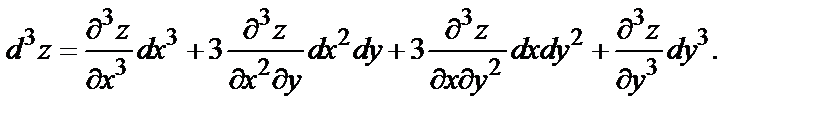
Дифференцирование неявных функций
Производная неявной функции 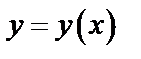 , заданной с помощью уравнения
, заданной с помощью уравнения 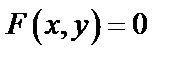 , где
, где 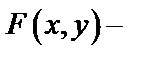 дифференцируемая функция переменных
дифференцируемая функция переменных 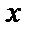 и
и 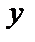 , может быть вычислена по формуле
, может быть вычислена по формуле
|
|
|
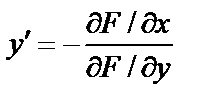 при условии
при условии 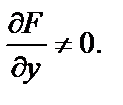 (7.2)
(7.2)
Производные высших порядков неявной функции можно найти последовательным дифференцированием указанной формулы, рассматривая при этом 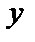 как функцию от
как функцию от 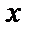 .
.
Аналогично, частные производные неявной функции двух переменных  , заданной с помощью уравнения
, заданной с помощью уравнения 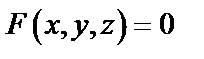 , где
, где 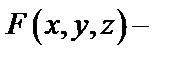 дифференцируемая функция переменных
дифференцируемая функция переменных 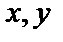 и
и 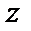 , могут быть вычислены по формулам
, могут быть вычислены по формулам
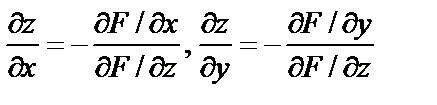 при условии
при условии 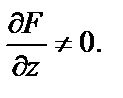 (7.3)
(7.3)
Экстремум функции
Функция 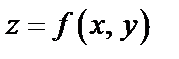 имеет максимум (минимум) в точке
имеет максимум (минимум) в точке 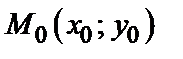 , если значение функции в этой точке больше (меньше), чем ее значение в любой другой точке
, если значение функции в этой точке больше (меньше), чем ее значение в любой другой точке  некоторой окрестности точки
некоторой окрестности точки 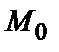 , т.е.
, т.е. 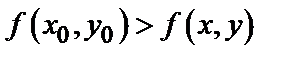 [соответственно
[соответственно 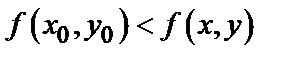 ] для всех точек
] для всех точек 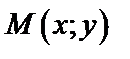 , удовлетворяющих условию
, удовлетворяющих условию 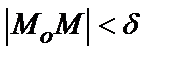 , где
, где 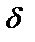
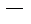 достаточно малое положительное число.
достаточно малое положительное число.
Максимум или минимум функции называется ее экстремумом. Точка 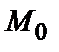 , в которой функция имеет экстремум, называется точкой экстремума.
, в которой функция имеет экстремум, называется точкой экстремума.
Если дифференцируемая функция 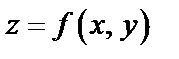 достигает экстремума в точке
достигает экстремума в точке 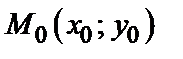 , то ее частные производные первого порядка в этой точке равны нулю, т.е.
, то ее частные производные первого порядка в этой точке равны нулю, т.е.
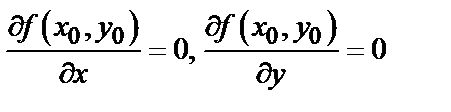
(необходимые условия экстремума).
Точки, в которых частные производные равны нулю, называются стационарными точками. Не всякая стационарная точка является точкой экстремума.
|
|
|
Пусть 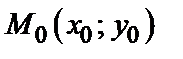
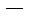 стационарная точка функции
стационарная точка функции 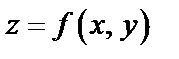 . Обозначим
. Обозначим

и составим дискриминант  Тогда:
Тогда:
а) если 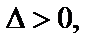 то функция имеет в точке
то функция имеет в точке 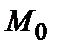 экстремум, а именно максимум при
экстремум, а именно максимум при 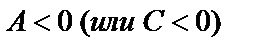 и минимум при
и минимум при 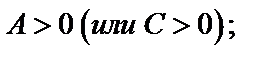
б) если 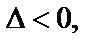 то в точке
то в точке 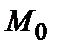 экстремума нет (достаточные условия наличия или отсутствия экстремума);
экстремума нет (достаточные условия наличия или отсутствия экстремума);
в) если 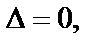 то требуется дальнейшее исследование (сомнительный случай).
то требуется дальнейшее исследование (сомнительный случай).
Решение типового задания
Пример 1.Дана функция 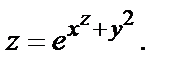 Найти частные производные первого порядка
Найти частные производные первого порядка 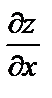 и
и 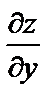 .
.
Решение.
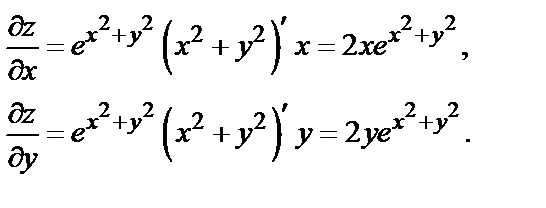
Пример 2. Дана функция 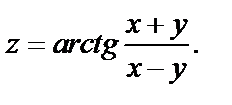 Найти dz.
Найти dz.
Решение.
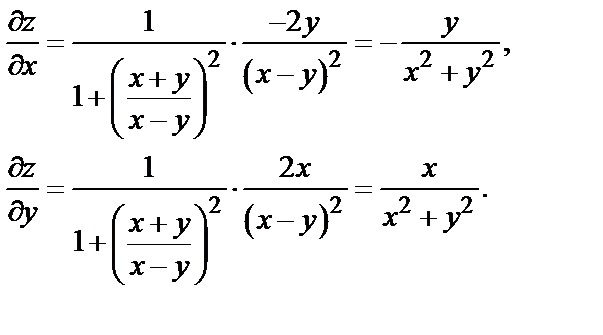
Следовательно, 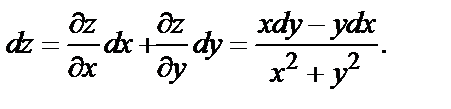
Пример 3. Вычислить приближенно 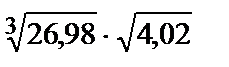 .
.
Решение. Рассмотрим функцию 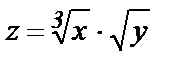 . Тогда
. Тогда 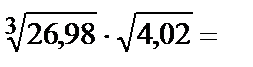
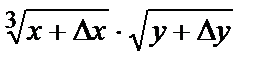 , где
, где  .
.
Воспользуемся формулой (*), предварительно найдя 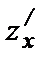 и
и 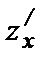 :
: 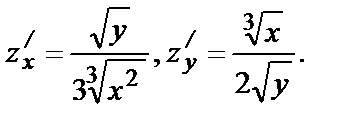 Вычислим значения функции и частных производных в точке (27, 4):
Вычислим значения функции и частных производных в точке (27, 4): 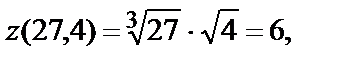
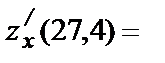

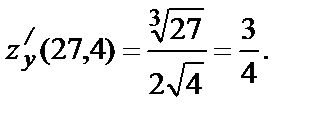
Следовательно,  .
.
Пример 4. Вычислить приближенно 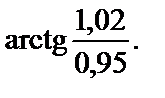
Решение. Рассмотрим функцию 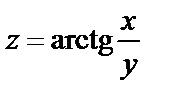 . Тогда
. Тогда 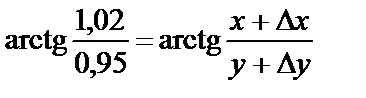 , где
, где 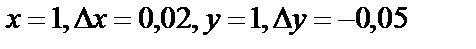 .
.
Воспользуемся формулой (*), предварительно найдя 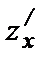 и
и 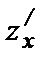 :
: 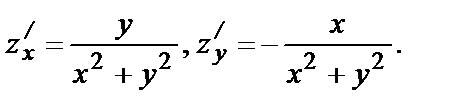 Вычислим значения функции и частных производных в точке (1, 1):
Вычислим значения функции и частных производных в точке (1, 1):
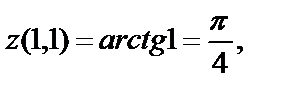
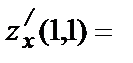
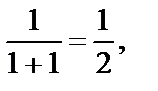
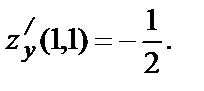
Следовательно, 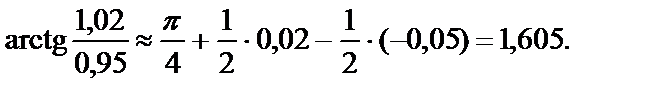
Пример 5. 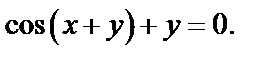 Найти
Найти 
Решение. Здесь 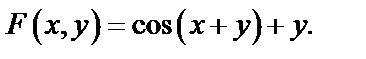
Найдем 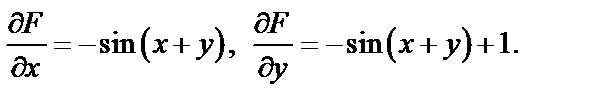
Следовательно,
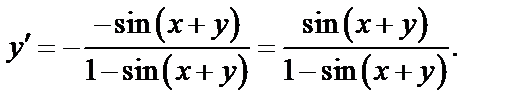
Пример 6. 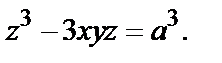 Найти
Найти 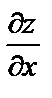 и
и 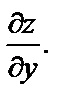
Решение. Здесь 
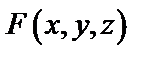 =
= 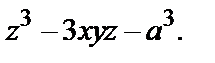
Находим 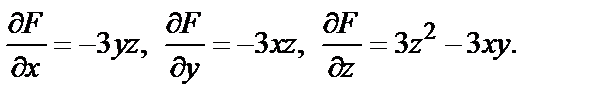
Тогда 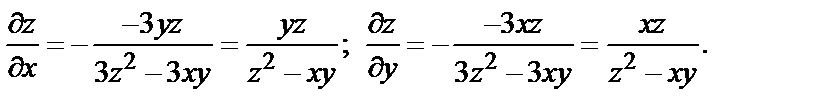
Пример 7. Найти экстремум функции 
Решение. Находим частные производные первого порядка: 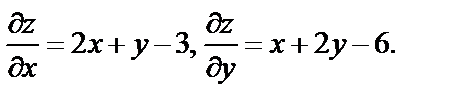 Воспользовавшись необходимыми условиями экстремума, находим стационарные точки:
Воспользовавшись необходимыми условиями экстремума, находим стационарные точки:
|
|
|
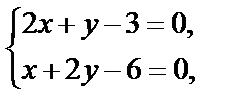 откуда
откуда 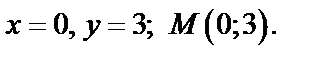
Находим значения частных производных второго порядка в точке M:
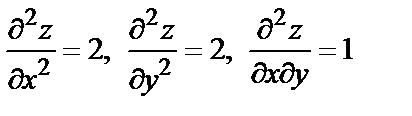
и составляем дискриминант 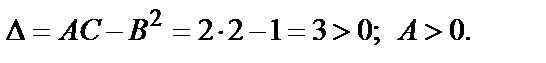 Следовательно, в точке
Следовательно, в точке 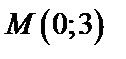 заданная функция имеет минимум. Значение функции в этой точке
заданная функция имеет минимум. Значение функции в этой точке 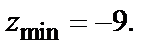
Пример 8. Найти экстремум функции
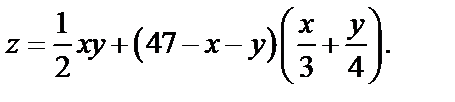
Решение. Находим частные производные первого порядка:
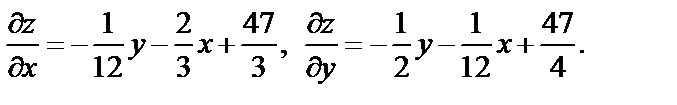
Воспользовавшись необходимыми условиями экстремума, находим стационарные точки:
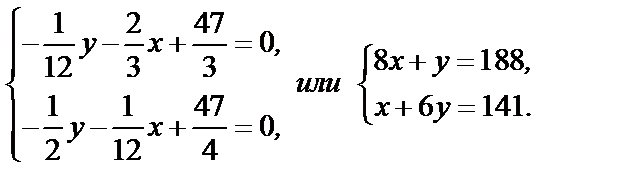
Отсюда x=21, y=20; стационарная точка 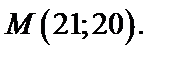
Найдем значения вторых производных в точке M: 
Тогда 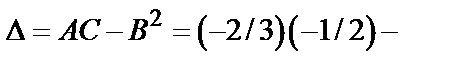
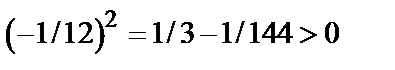 .
.
Так как A<0, то в точке 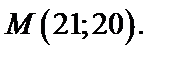 функция имеет максимум:
функция имеет максимум: 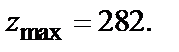
Задачи № 241-270:
Найти частные производные первого порядка 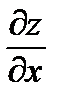 и
и  от функции
от функции 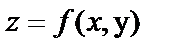 :
:
241. 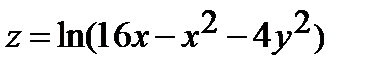
| 256. 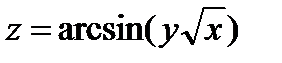
|
242. 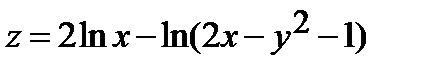
| 257. 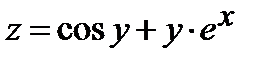
|
243. 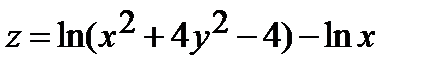
| 258. 
|
244. 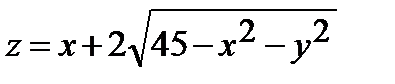
| 259. 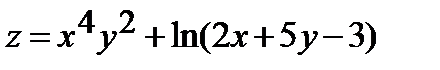
|
245. 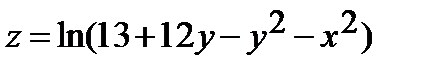
| 260. 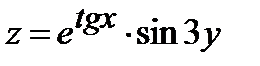
|
246. 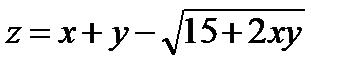
| 261. 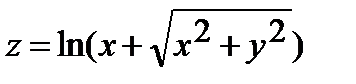
|
247. 
| 262. 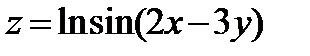
|
248. 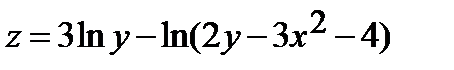
| 263. 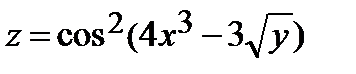
|
249. 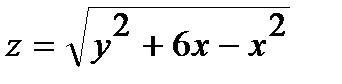
| 264. 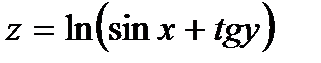
|
250. 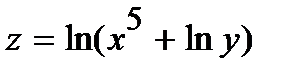
| 265. 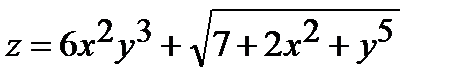
|
251. 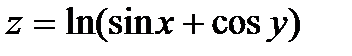
| 266. 
|
252. 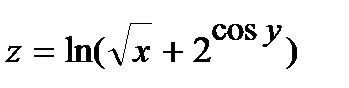
| 267. 
|
253. 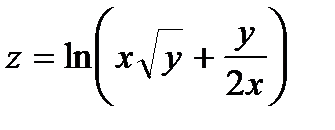
| 268. 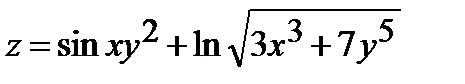
|
254. 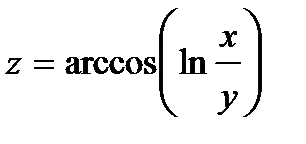
| 269. 
|
255. 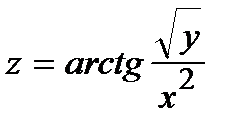
| 270. 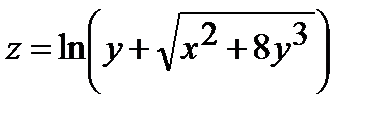
|
Задачи № 271-300:
Вычислить приближенное значение функции 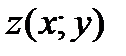 в точке А.
в точке А.
271. 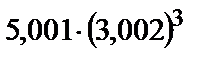
| 286. 
|
272. 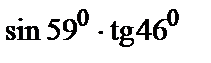
| 287. 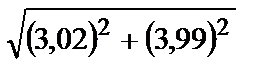
|
273. 
| 288. 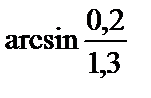
|
274. 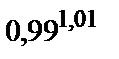
| 289. 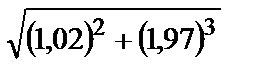
|
275. 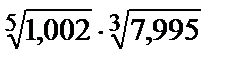
| 290. 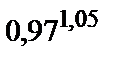
|
276. 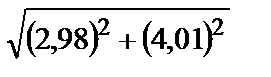
| 291. 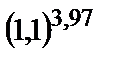
|
277. 
| 292. 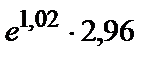
|
278. 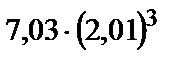
| 293. 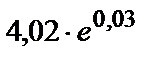
|
279. 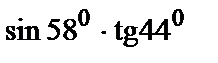
| 294. 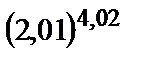
|
280. 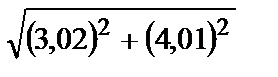
| 295. 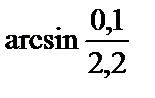
|
281. 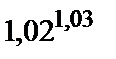
| 296. 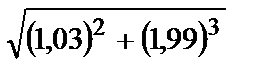
|
282. 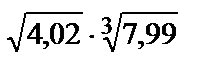
| 297. 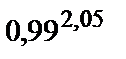
|
283. 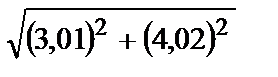
| 298. 
|
284. 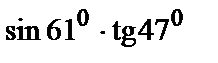
| 299. 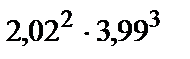
|
285. 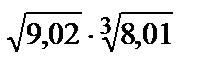
| 300. 
|
Задачи № 301-330:
Найти производную 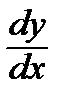 от неявной функции, заданной уравнением:
от неявной функции, заданной уравнением:
301. 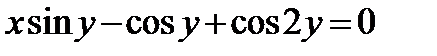
| 316. 
|
302. 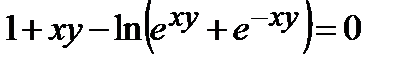
| 317. 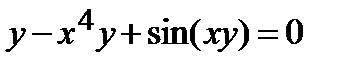
|
303. 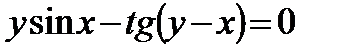
| 318. 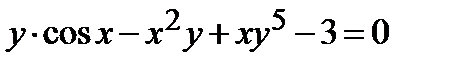
|
304. 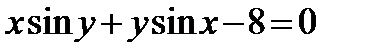
| 319. 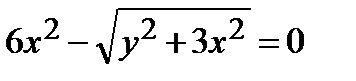
|
305. 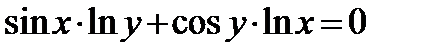
| 320. 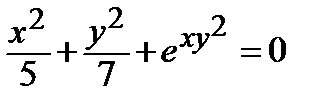
|
306. 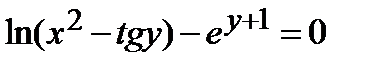
| 321. 
|
307. 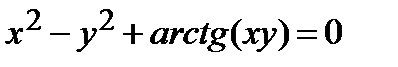
| 322. 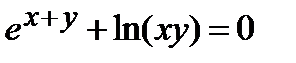
|
308. 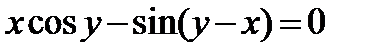
| 323. 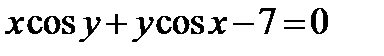
|
309. 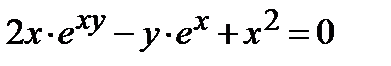
| 324. 
|
310. 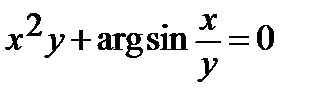
| 325. 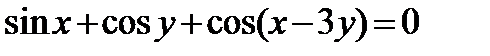
|
311. 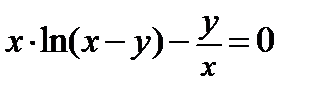
| 326. 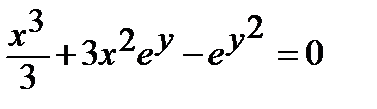
|
312. 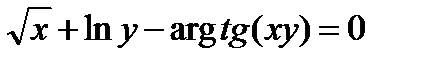
| 327. 
|
313. 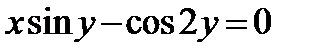
| 328. 
|
314. 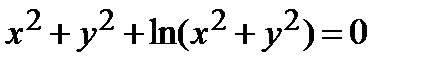
| 329. 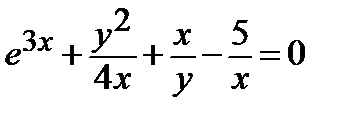
|
315. 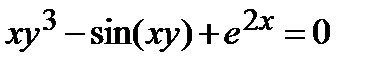
| 330. 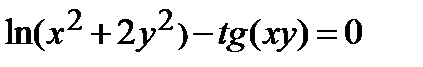
|
Задачи №331-360:
Найти экстремум функции двух переменных  :
:
331. 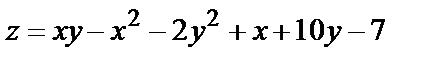
|
332. 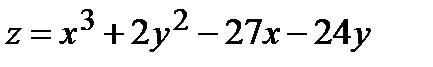
|
333. 
|
334. 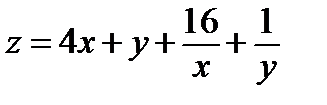
|
335. 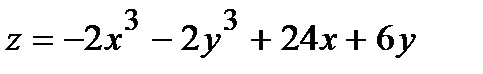
|
336. 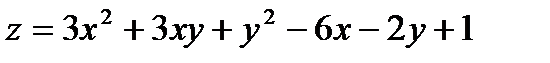
|
337. 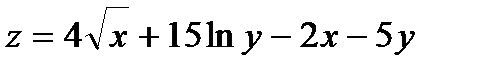
|
338. 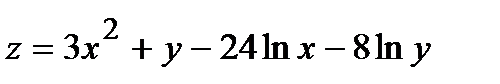
|
339. 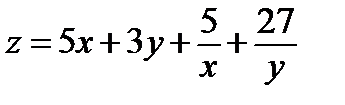
|
340. 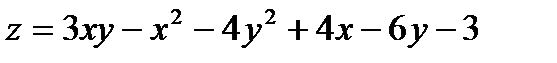
|
341. 
|
342. 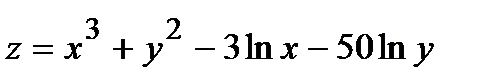
|
343. 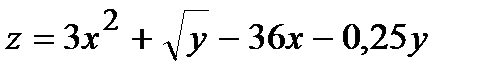
|
344. 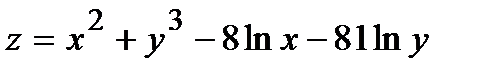
|
345. 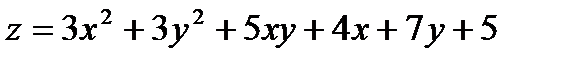
|
346. 
|
347. 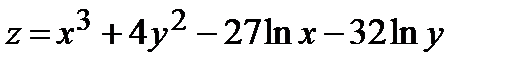
|
348. 
|
349. 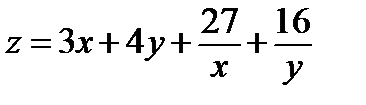
|
350. 
|
351. 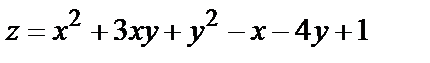
|
352. 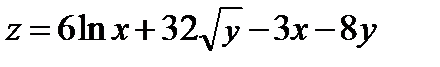
|
353. 
|
354. 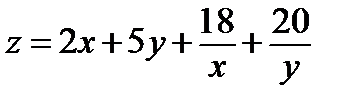
|
355. 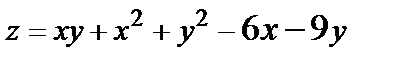
|
356. 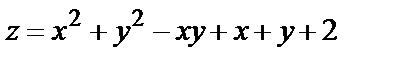
|
357. 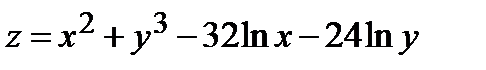
|
358. 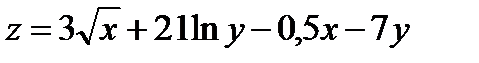
|
359. 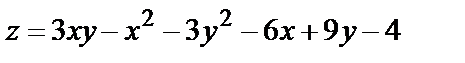
|
360. 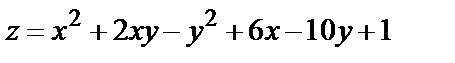
|
ТЕМА 10 ТЕОРИЯ Вероятностей
Теория вероятностей –математическая наука, изучающая закономерности случайных явлений. Под случайными явлениями понимаются явления с неопределенным исходом, происходящие при неоднократном воспроизведении определенного комплекса условий.
10.1 Элементы комбинаторики
В теории вероятностей часто приходится иметь дело с задачами, в которых необходимо подсчитывать число возможных способов каких-либо действий. Задачи такого типа называются комбинаторными, а раздел математики, занимающийся решениями таких задач, - комбинаторикой.
Факториалом натурального числа n называется число
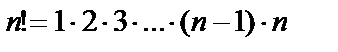 . (10.1)
. (10.1)
По определению, факториалом нуля является единица:
0!=1.
Рассмотрим некоторое множество S , состоящее из n различных элементов. Пусть  . Назовём множество, состоящее из k элементов, упорядоченным, если каждому элементу этого множества поставлено в соответствие число от 1 до k , причём различным элементам множества соответствуют разные числа.
. Назовём множество, состоящее из k элементов, упорядоченным, если каждому элементу этого множества поставлено в соответствие число от 1 до k , причём различным элементам множества соответствуют разные числа.
Размещениями из n элементов по kназываются упорядоченные подмножества множества S,состоящие из k различных элементов и отличающиеся друг от друга составом элементов или порядком их расположения.
Число размещений из n элементов по k равно
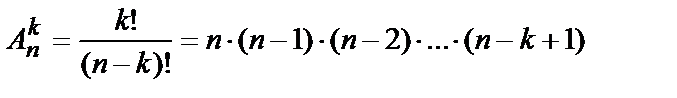 . (10.2)
. (10.2)
Перестановками из n элементовназываются размещения из n элементов по n,т. е. упорядоченные подмножества множества S, состоящие из всех элементов данного множества и отличающиеся друг от друга только порядком их расположения.
Число перестановок из n элементов равно
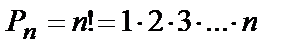 . (10.3)
. (10.3)
Сочетаниями из n элементов по kназываются подмножества множества S , состоящие из k различных элементов и отличающиеся друг от друга только составом элементов.
Число сочетаний из n элементов по k равно
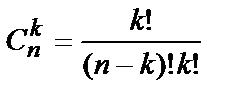 .
.  (10.4)
(10.4)
Размещениями с повторениями из n элементов по k называются упорядоченные подмножества множества S , состоящие из k элементов, среди которых могут оказаться одинаковые, и отличающиеся друг от друга составом элементов или порядком их расположения.
Число размещений с повторениями из n элементов по k равно
 (10.5)
(10.5)
Сочетаниями с повторениями из n элементов по kназываются подмножества множества S,состоящие из k элементов, среди которых могут оказаться одинаковые, и отличающиеся друг от друга только составом элементов.
Число сочетаний с повторениями из n элементов по k равно
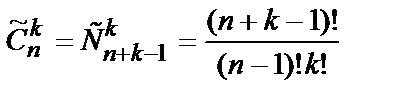 . (10.6)
. (10.6)
Если во множестве S, состоящем из n элементов, есть только m различных элементов, то перестановками с повторениями из n элементовназываются упорядоченные подмножества множества S , в которые первый элемент множества S входит n1 раз, второй элемент — n2 раз и так до
m -го элемента, который входит nm раз (n1 +n2+…+nm = n).
Число перестановок с повторениями из n элементов, в которые первый элемент множества S входит n1 раз, второй элемент — n2 раз и так до m -го элемента, который входит nm раз(n1 +n2 +…+nm = n), равно
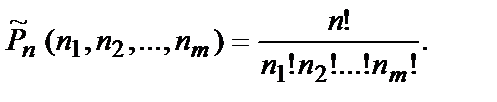 (10.7)
(10.7)
Дата добавления: 2018-05-12; просмотров: 391; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
