Метод вариации произвольной постоянной
(метод Лагранжа):
1) находим общее решение соответствующего линейного однородного уравнения 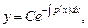
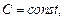
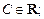
2) общее решение линейного неоднородного уравнения ищем в виде
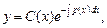 (22.17)
(22.17)
где 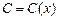 – некоторая функция, которую необходимо найти;
– некоторая функция, которую необходимо найти;
3) подставляем функцию (22.17) в уравнение (22.15) и находим функцию C (x):
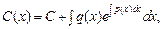
где С – произвольная постоянная;
4) общее решение уравнения (22.15) записываем в виде
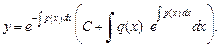 (22.18)
(22.18)
Метод Бернулли:
1) ищем общее решение дифференциального уравнения (22.15) в виде
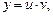 (22.19)
(22.19)
где 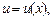
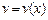 – некоторые функции, которые надо найти;
– некоторые функции, которые надо найти;
2) подставляем функцию (22.19) и ее производную в уравнение (22.15), получаем:
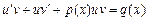 или
или
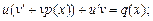 (22.20)
(22.20)
3) функцию v (x) подбираем как частное решение (при 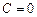 ) дифференциального уравнения
) дифференциального уравнения
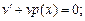 (22.21)
(22.21)
4) при условии (22.21) решаем уравнение (22.20), которое приобретает вид

как дифференциальное уравнение с разделяющимися переменными (находим его общее решение);
5) общее решение исходного уравнения (22.15) записываем как произведение найденных функций u (x) и v (x), т. е. в виде (22.19).
З а м е ч а н и е. При решении дифференциальных уравнений методами Лагранжа и Бернулли реализуем «пошагово» описанные алгоритмы.
Уравнение вида
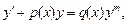 (22.22)
(22.22)
где  называется уравнением Бернулли.
называется уравнением Бернулли.
Если 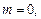 то это линейное дифференциальное уравнение, если
то это линейное дифференциальное уравнение, если 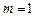 – уравнение с разделяющимися переменными.
– уравнение с разделяющимися переменными.
Если 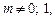 то при решении таких уравнений также применяют метод Лагранжа или метод Бернулли.
то при решении таких уравнений также применяют метод Лагранжа или метод Бернулли.
Пример 1. Решить уравнение двумя способами:
|
|
|
1) 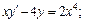 2)
2) 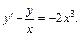
Решение. 1) Преобразуем уравнение (полагая 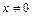 ) к виду линейного неоднородного дифференциального уравнения
) к виду линейного неоднородного дифференциального уравнения

1-й способ. Решим методом Лагранжа. Найдем общее решение соответствующего ему однородного уравнения 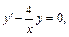
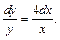
Интегрируем и получаем:
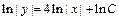
или 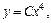 где
где 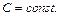
Общее решение исходного дифференциального уравнения будем искать в виде
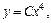 (22.23)
(22.23)
где 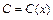 – функция от переменной x.
– функция от переменной x.
Найдем C (x). Для этого дифференцируем (22.23):
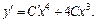
Подставляем функцию (22.23) и ее производную в исходное дифференциальное уравнение:
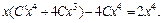
Упрощаем полученное уравнение и решаем относительно 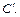 Получаем:
Получаем: 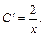
Далее интегрируем:
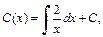
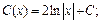
 Подставляем найденное выражение вместо C в равенство (22.23). Тогда общее решение исходного дифференциального уравнения имеет вид
Подставляем найденное выражение вместо C в равенство (22.23). Тогда общее решение исходного дифференциального уравнения имеет вид 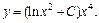
2-й способ. Ищем общее решение исходного уравнения в виде (22.19). После подстановки получим:
 (22.25)
(22.25)
Подбираем функцию v как частное решение (при 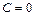 ) уравнения
) уравнения
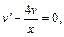 т. е.
т. е. 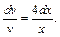
Вследствие интегрирования имеем:
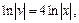
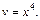
Подставляем найденную функцию v в (22.25), получаем:
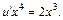
Находим общее решение последнего уравнения, разделяя переменные:
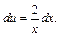
Интегрируем и получаем:
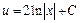 или
или 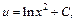 где
где 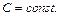
Тогда общее решение исходного уравнения имеет вид (в соответствии с (22.19)):
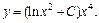
Вывод: в данном примере решение методом Бернулли (2-й способ) оказалось более рациональным, так как быстрее привело к ответу.
|
|
|
2) 1-й способ. Решим уравнение методом Лагранжа. Находим общее решение соответствующего ему однородного уравнения
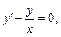 т. е.
т. е. 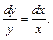
Интегрирование дает:
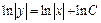 или
или 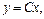
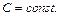
Общее решение исходного дифференциального уравнения будем искать в виде
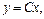 (22.26)
(22.26)
где 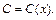
Дифференцируем функцию (22.26):
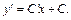
Подставляем функцию (22.26) и ее производную в исходное дифференциальное уравнение:
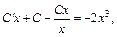
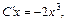
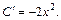 Интегрирование последнего равенства дает нам
Интегрирование последнего равенства дает нам 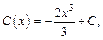 где
где 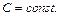
Подставляем найденное выражение вместо C (x) в (22.26). Получаем общее решение заданного уравнения:
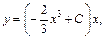 т. е.
т. е. 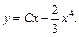
2-й способ. Ищем общее решение в виде 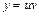 (метод Бернулли), где
(метод Бернулли), где 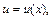
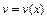 – функции, которые надо найти. Вычисляем производную
– функции, которые надо найти. Вычисляем производную 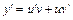 и подставляем ее вместе с функцией
и подставляем ее вместе с функцией 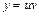 в исходное уравнение. Получаем:
в исходное уравнение. Получаем:
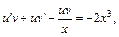 т. е.
т. е.
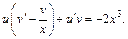 (22.27)
(22.27)
Согласно методу, полагаем 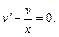 Из этого уравнения (как из дифференциального уравнения с разделяющимися переменными) найдем функцию v (x). Интегрируем равенство
Из этого уравнения (как из дифференциального уравнения с разделяющимися переменными) найдем функцию v (x). Интегрируем равенство 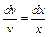 и находим
и находим 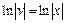 (константу C полагаем равной нулю).
(константу C полагаем равной нулю).
Из последнего уравнения имеем: 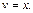 Возвращаемся к уравнению (22.27). С учетом равенства нулю выражения в скобках и найденной функции v (x) оно имеет вид:
Возвращаемся к уравнению (22.27). С учетом равенства нулю выражения в скобках и найденной функции v (x) оно имеет вид:
 или
или 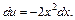
Интегрируем последнее равенство. Получаем:
|
|
|

где 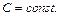
Тогда общее решение 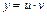 исходного дифференциального уравнения имеет вид:
исходного дифференциального уравнения имеет вид:
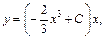 т. е. приходим к ответу:
т. е. приходим к ответу:
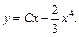
Вывод: более рациональным оказался метод Лагранжа (1-й способ), так как быстрее привел к общему решению исходного дифференциального уравнения.
Пример 2. Найти частное решение дифференциального уравнения:
1) 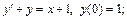 2)
2) 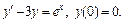
Решение. 1. Найдем общее решение методом Лагранжа. Рассмотрим соответствующее однородное уравнение
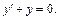
Решаем его как дифференциальное уравнение с разделяющимися переменными, т. е.
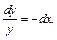
Его решением является 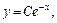 где
где 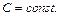
Ищем общее решение заданного дифференциального уравнения в виде
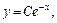 (22.28)
(22.28)
где 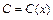 – некоторая функция.
– некоторая функция.
Найдем функцию 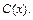 Дифференцируем выражение (22.28):
Дифференцируем выражение (22.28):
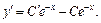
Подставляем найденную производную и функцию (22.28) в заданное уравнение, получаем:
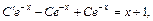 т. е.
т. е.
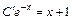 или
или 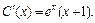
Тогда  Интегрируя по частям, получим:
Интегрируя по частям, получим:
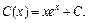
где 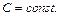
Найденное выражение С (x) подставляем в равенство (22.28), получаем: 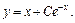
Найдем частное решение, используя начальное условие. Если 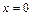 и
и 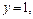 то
то 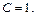 Значит, частное решение имеет вид:
Значит, частное решение имеет вид: 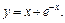
2) Найдем общее решение методом Бернулли, т. е. в виде 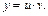
После подстановки производной 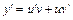 и самой функции
и самой функции 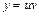 в исходное дифференциальное уравнение получаем:
в исходное дифференциальное уравнение получаем:
 т. е.
т. е.
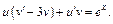 (22.29)
(22.29)
Полагаем 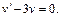 Интегрируем это уравнение как дифференциальное уравнение с разделяющимися переменными и находим v (x):
Интегрируем это уравнение как дифференциальное уравнение с разделяющимися переменными и находим v (x):
|
|
|

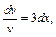
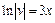 (полагаем
(полагаем 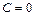 ) или
) или 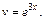
Возвращаемся к дифференциальному уравнению (22.29):
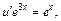
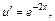
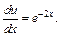
Имеем уравнение 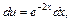 которое интегрируем, и получаем:
которое интегрируем, и получаем:

где 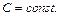
Тогда общее решение заданного дифференциального уравнения имеет вид:
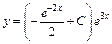 или
или 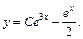
Найдем частное решение, используя начальное условие. Если 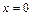 и
и  то
то 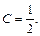 Значит, частное решение имеет вид:
Значит, частное решение имеет вид: 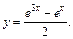
Пример 3. Решить уравнение:
1) 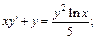 2)
2) 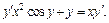
Решение. 1) Это уравнение Бернулли. Будем искать общее решение методом Бернулли, т. е. в виде 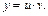
После подстановки получим:
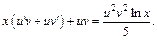
После упрощения имеем:
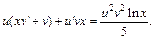 (22.30)
(22.30)
Полагая 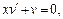 находим функцию
находим функцию 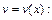
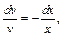
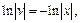
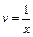 (полагаем
(полагаем 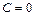 ).
).
Подставляем найденную функцию 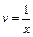 в дифференциальное уравнение (22.30):
в дифференциальное уравнение (22.30):
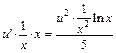 или
или 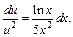
Интегрируем последнее уравнение:
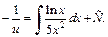
После интегрирования по частям получаем:
 откуда
откуда 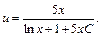
Тогда общее решение заданного дифференциального уравнения имеет вид:
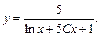
2) Запишем заданное уравнение в виде
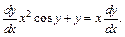
Это уравнение не является линейным дифференциальным уравнением вида (22.15) или уравнением Бернулли вида (22.22). Умножим заданное уравнение на 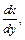 получим:
получим: 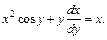
Разделим его на y (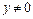 ) и получим уравнение Бернулли
) и получим уравнение Бернулли
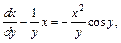 (22.31)
(22.31)
решением которого является функция 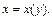 Ищем общее решение последнего дифференциального уравнения в виде
Ищем общее решение последнего дифференциального уравнения в виде 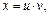 где
где 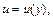
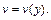 Находим производную
Находим производную 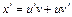 и подставляем ее вместе с функцией в уравнение (22.31):
и подставляем ее вместе с функцией в уравнение (22.31):
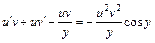 или
или
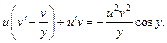 (22.32)
(22.32)
Найдем v (y), решая уравнение
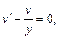 т. е.
т. е. 
Интегрирование дает:
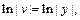 т. е.
т. е. 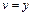 (полагаем
(полагаем 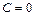 ).
).
Подставляем найденную функцию v в уравнение (22.32):
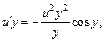
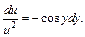 Интегрируя последнее уравнение, получим:
Интегрируя последнее уравнение, получим:
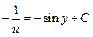 или
или 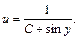
Получаем общее решение (общий интеграл) заданного дифференциального уравнения:
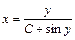 или
или 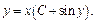
Задания
I уровень
1.1. Решите уравнение:
1)  2)
2)  3)
3) 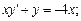 4)
4) 
1.2. Решите задачу Коши:
1) 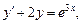
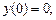 2)
2) 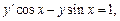
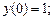
3) 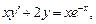
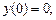 4)
4) 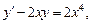
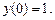
II уровень
2.1. Решите уравнение:
1) 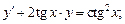 2)
2) 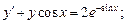
3) 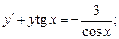 4)
4) 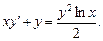
2.2. Решите задачу Коши:
1) 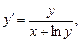

2) 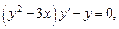
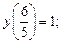
3) 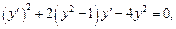

4) 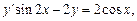
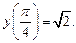
III уровень
3.1. Составьте уравнение кривой 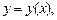 проходящей через точку A (a, a) и обладающей свойством: если в любой точке N (x, y) кривой с ординатой, равной | BN | (рис. 22.2) провести касательную до пересечения с осью ординат в точке С, то площадь трапеции OCNB будет постоянной и равна
проходящей через точку A (a, a) и обладающей свойством: если в любой точке N (x, y) кривой с ординатой, равной | BN | (рис. 22.2) провести касательную до пересечения с осью ординат в точке С, то площадь трапеции OCNB будет постоянной и равна 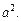
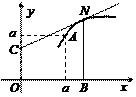 |
Рис. 22.2
3.2. Составьте уравнение кривой 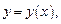 проходящей через точку
проходящей через точку 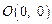 и обладающей свойством: середина отрезка ее нормали, заключенного между любой точкой кривой и осью абсцисс, лежит на параболе
и обладающей свойством: середина отрезка ее нормали, заключенного между любой точкой кривой и осью абсцисс, лежит на параболе 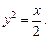
Дата добавления: 2015-12-17; просмотров: 20; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
