Метод конечных элементов (МКЭ)
Для сложных конструкций, которые приходится рассчитывать, число базисных функций k в методе Ритца (N) должно быть весьма большим, чтобы обеспечить приемлемую точность решения. Поэтому матрица жесткости K может достичь, вообще говоря, очень больших размеров (в ней N 2 элементов), затрудняя решение системы уравнений (11) и само ее построение. Оказывается, можно выбрать такой набор базисных функций (в самом методе Ритца не указывается, как именно их выбирать), что лишь небольшая часть элементов матрицы K будет отлична от нуля. Применяя специальные схемы хранения и алгоритмы, можно достичь значительной эффективности благодаря этой разреженности матрицы. Метод конечных элементов, широко используемый в расчетах (в частности, в ANSYS), является частным случаем метода Ритца. Этот метод указывает, как построить базисные функции k, чтобы обеспечить разреженность матрицы системы K.
В МКЭ расчетная область разбивается на подобласти (конечные элементы) определенной формы. В каждом конечном элементе имеются узлы и т. н. функции формы. Решение задачи на отдельном элементе аппроксимируется линейной комбинацией функций форм; коэффициенты этой линейной комбинации — значения решения в узлах:
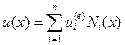(12)
Здесь n — число узлов в конечном элементе, i — номер узла в элементе (т. н. локальный номер),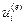 
— значение неизвестной в i -том узле, Ni (x) — функция формы, соответствующая i -тому узлу. Важное свойство функций формы состоит в том, что они равны единице в соответствующем им узле и нулю в остальных узлах элементов:
|
|
|
(
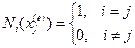
— координаты узлов). В этом легко убедиться, вычислив по формуле (12) значение неизвестной функции в узлах.
Соседние конечные элементы модели соприкасаются друг с другом и, таким образом, имеют общие узлы. Каждый узел может принадлежать одновременно нескольким элементам. Различают локальный номер узла (то есть его номер в некотором элементе) и глобальный номер, свой для каждого узла. Каждый узел имеет один глобальный номер и, вообще говоря, несколько локальных (столько, скольким элементам узел принадлежит).
Если в методе Ритца смысл коэффициентов ck не оговаривается, то в МКЭ, напротив, он четко определен — это uk, значения искомой функции в узлах (здесь k — глобальный номер узла). Каждому uk соответствует базисная функция k из метода Ритца. На каждом элементе, содержащем k -тый узел, эта функция равна функции формы Ni, соответствующей k -тому узлу; она равна нулю на всех остальных элементах (рис. 2). Таким образом, k отлична от нуля лишь на небольшой части области вблизи k -того узла. Благодаря этому лишь немногие элементы матрицы K отличны от нуля: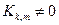 
только если k -тый и m -тый узлы принадлежат одному и тому же конечному элементу (см. формулу (9)).
|
|
|
Чтобы найти матрицу системы K и правую часть R, удобно ввести в рассмотрение аналогичные матрицы K ( e ) и R ( e ) для одного элемента — т. н. локальные матрицы. Каждая локальная матрица K ( e ) (соответственно, R ( e )) дает свой вклад в глобальную матрицу K. (соответственно, R ( e )).
Проиллюстрируем сказанное на нашей задаче о растяжении стержня. Разобьем стержень на 5 двухузловых конечных элементов длины l /5 (рис. 3). В качестве функций формы на каждом элементе возьмем пару линейных функций. Локальные матрицы жесткости K ( e ) всех элементов будут одинаковыми, и, как нетрудно подсчитать по формуле (9), равными
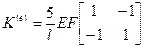
Столбцы правых частей также будут одинаковыми, так как распределенная сила p постоянна:), за исключением R (5) — в этот столбец попадет еще сосредоточенная сила P:
Сосредоточенные силы (такие, как P) обычно задаются в узлах и добавляются непосредственно в глобальный столбец узловых сил, так как их трудно отнести к какому-либо конечному элементу. Теперь нетрудно собрать глобальные матрицы K и R:
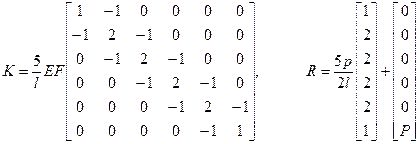
Отметим, что матрица K оказалась не полностью заполненной, а трехдиагональной, то есть весьма разреженной. Эта характерная для МКЭ разреженнось, как уже отмечалось, решающим образом влияет на эффективность численного решения задачи.
|
|
|
До сих пор оставалось в стороне граничное условие (1) — заделка. Как говорилось в предыдущем разделе, обычно требуют выполнения кинематических граничных условий для всех базисных функций k. Очевидно, в нашем примере 1 не удовлетворяет условию (1), так как 1(0) = 1. В МКЭ часто применяют специальный прием, чтобы удовлетворить кинематическим граничным условиям. Допустим, в узле с номером s задано перемещение us. Вместо того, чтобы требовать равенства нулю всех k в узле s, после построения матриц K и R полагают Ks,s = A, Rs = Aus где A — очень большое число (много больше остальных элементов матрицы K). Это приводит к тому, что кинематические граничные условия выполняются почти точно. В нашем примере, чтобы учесть условие заделки, надо положить K 1,1 = A, R 1 = 0. Число A можно принять равным 1010E.
Дата добавления: 2015-12-20; просмотров: 16; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!