Вариационная постановка
Всякая задача математической физики допускает обычно две постановки: дифференциальную (ее мы рассмотрели выше) и вариационную. Метод конечных элементов (МКЭ) опирается на вариационную постановку, которая состоит в следующем. На расчетной области (в данном случае — отрезке [0, l ]) вводится пространство U функций, обладающих достаточной гладкостью и, грубо говоря, пригодных для достаточно точной аппроксимации решения задачи, а также, возможно, удовлетворяющих некоторым граничным условиям. В нашей задаче таким пространством U будет множество дифференцируемых функций (x), определенных на отрезке [0, l ] и равных нулю при x = 0, то есть удовлетворяющих кинематическому граничному условию (2). Далее, вводится в рассмотрение функционал J (). Функционал — это отображение множества функций во множество вещественных чисел. Вариационная постановка задачи сводится к тому, чтобы подобрать функционал J, обладающий свойством экстремальности на точном решении задачи. Если функционал выпуклый, то в точке экстремума он принимает наименьшее или наибольшее значение. В нашей задаче таким функционалом является потенциальная энергия системы (функционал Лагранжа):
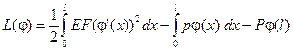(6)
Здесь первое слагаемое — энергия упругой деформации стержня, остальные два — работа нагрузок. Решение вариационной задачи состоит в поиске такой функции (x) из пространства U, на которой функционал принимает наименьшее значение. Эта функция и будет решением задачи — полем перемещений u (x) в сечениях стержня.
|
|
|
Убедимся, что вариационная и дифференциальная постановки нашей задачи эквивалентны друг другу. Для этого вспомним, что в точке экстремума функционала его вариация равна нулю. (Вариация L () функционала L () — это главная линейная часть его изменения при малом изменении функции ; (x), как и (x) — функция из пространства U.) Найдем L (u) и, считая u решением, приравняем L к нулю. Варьируя (6) (правила варьирования напоминают правила дифференцирования), получим:
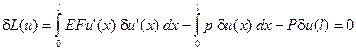
Избавимся от вариации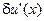 
в первом интеграле, взяв его по частям. После перегруппировки слагаемых получим
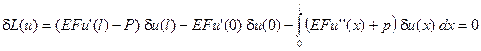
Это выражение должно быть равно нулю для любой функции 
из пространства U. Как показывается в вариационном исчислении, такое возможно только при равенстве нулю каждого слагаемого по отдельности. Второе слагаемое равно нулю автоматически, так как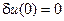 
— так было выбрано пространство функций. Вариация 
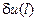произвольна, поэтому в первом слагаемом равен нулю первый множитель — получили граничное условие (3). Третье слагаемое равно нулю при любом тогда и только тогда, когда равно нулю подынтегральное выражение — то есть, выполняется уравнение (1). Таким образом, мы показали эквивалентность вариационной и дифференциальной постановок данной задачи.
|
|
|
Метод Ритца
Математическая физика рассматривает задачи с бесконечным числом неизвестных. Например, в задаче о растяжении стержня неизвестной величиной является перемещение в каждом сечении. Чтобы получить возможность численного решения таких задач, необходимо произвести дискретизацию, то есть заменить модель с бесконечным числом неизвестных адекватной моделью с конечным числом неизвестных. Вариационная постановка привлекательна именно в связи с возможностью осуществлять такую дискретизацию простым и естественным путем. Эта возможность — в выборе пространства U функций, в котором разыскивается решение задачи.
Решение любой задачи математической физики можно с достаточной точностью аппроксимировать линейной комбинацией конечного числа заранее заданных (т. н. базисных) функций k (x) k = 1,2,… N. Неизвестными задачи становятся множители при базисных функциях в этой линейной комбинации. Чем большая требуется точность, тем больше базисных функций надо взять. Выбранные базисные функции и определяют пространство U — это будет их линейная оболочка (то есть множество всевозможных линейных комбинаций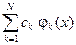 
с вещественными коэффициентами ck).
|
|
|
Например, при численном решении задачи о растяжении стержня рассматривается не всё пространство дифференцируемых функций (x), таких, что (0) = 0, а лишь некоторое его подпространство, пригодное для достаточно точной аппроксимации решения. В качестве базисных функций можно взять, скажем, полиномы xk, k = 1,2,… N.
Проиллюстрируем процедуру дискретизации на нашей задаче. Аппроксимируем перемещения сечений стержня линейной комбинацией базисных функций k:
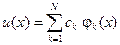(7)
Подставив аппроксимацию (7) в функционал (6), получим
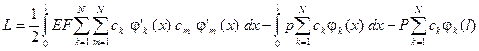
или, в матричной записи,
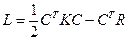(8)
Здесь C — столбец (высоты N) коэффициентов c 1, c 2,…, cN, K — матрица жесткости системы, состоящая из N строк и N столбцов, R — столбец (высоты N) узловых нагрузок, эквивалентных приложенным силам. Верхний индекс T обозначает транспонирование. Элементы матрицы K и столбца R вычисляются по формулам
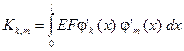, k, m = 1, 2, …, N (9)
, k = 1, 2, …, N (10)
Так как каждая функция из выбранного нами пространства определяется N коэффициентами c 1, c 2,…, cN, то функционал L превратился в функцию этих коэффициентов: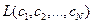 
. Как известно из теории функций нескольких переменных, его минимум достигается при равенстве нулю частных производных по всем аргументам: ¶ L /¶ c 1=0, ¶ L /¶ c 2=0, …, ¶ L /¶ cN =0. Таким образом, дифференцируя (8), получим условие минимальности функционала L, которое можно записать в виде
|
|
|
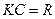(11)
Итак, мы перешли от исходного дифференциального уравнения и граничных условий
(1–3) к системе линейных алгебраических уравнений (11). Переход, который мы проделали, носит название метода Ритца. Систему (11) можно решать разнообразными численными методами. При этом обычно играет важную роль симметричность матрицы K (по построению) и ее положительная определенность (это следует из положительности потенциальной энергии).
Дата добавления: 2015-12-20; просмотров: 16; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!