Основные параметры конечно-элементных моделей и систем конечно-элементных уравнений

Модель	n	b	p
М–8/40/153			12 111
М–8/160/545			82 199

 

Решим указанные задачи, принимая 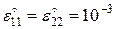. Компоненты средних тензоров микронапряжений представлены в табли­це 4.3.

Таблица 4.3

Средние напряжения в задачах о поперечном растяжении (МПа)

Задача	Модель
(1)	М–8/40/153	32,27	12,64	16,27
(1)	М–8/160/545	32,26	12,66	16,27
(2)	М–8/40/153	12,64	36,21	17,62
(2)	М–8/160/545	12,66	36,19	17,62

 

Из приведенных результатов следует:

1. Средние напряжения практически не изменились при пере­ходе от КЭ-модели 1-го уровня к КЭ-модели 2-го уровня (так называемое сгущение конечно-элементной сетки, “ h ”-сходимость)

 

Рис. 4.1. Конечно-элементная модель

2. Выполняется теорема взаимности Бетти:

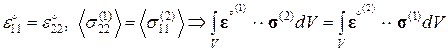
Определим эффективные модули Юнга и коэффициенты Пуас­сона, используя соотношения (3.1.9), (3.1.10), (4.1.1) и средние напряжения из таблицы 4.3 (модель M-8/160/545);

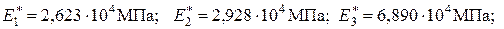
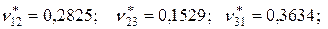
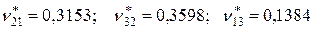
4.1.4. Эффективные коэффициенты линейного температурного расширения. Решим задачу о равномерном нагреве 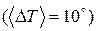ячейки периодичности при задании кинематико-статических граничных условий (3.2.3). Используем КЭ-модель 2-го уровня – M–8/160/545. Компоненты среднего тензора микро­напряжений имеют следующие значения:

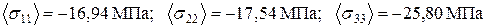
Используя соотношения (3.2.5), определим эффективные коэффициенты линейного температурного расширения:

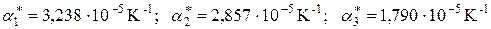
4.1.5. Эффективные модули сдвига. Для определения эффективного модуля сдвига 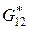решим задачу о поперечном сдвиге ячейки периодичности, находящейся в плоском деформированном состоянии, при задании кинематико-статических гра­ничных условий (3.4.12). Используя соотношение (3.4.15), определим эффективный модуль сдвига :

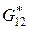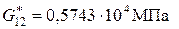
Для определения эффективных модулей сдвига 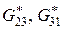решим две задачи о продольном сдвиге ячейки периодичности (антиплоская деформация) при задании смешанных граничных условий (3.4.16) и (3.4.20). Используя соотношения (3.4.19) и (3.4.21), определим эффективные модули сдвига :

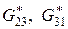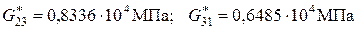
Отметим, что при решении указанных задач о попереч­ном сдвиге и продольном сдвиге использовались две конечно-элементные модели: M–8/40/153 и М–8/160/545; средние напряжения при переходе от КЭ-модели 1-го уровня к КЭ-модели 2-го уровня изменяются лишь в четвертой значащей цифре.

Макроскопически трансверсально-изотропная двухфазная гетерогенная среда. Эффективные модули Юнга, коэффициенты Пуассона, коэффициенты линейного температурного расширения и модули сдвига

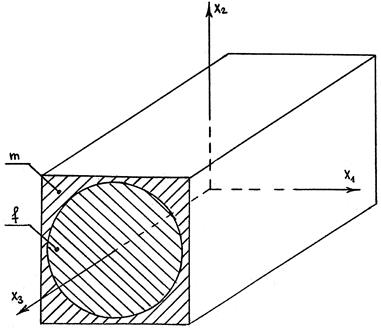
4.2.1. Представительный элемент объёма. Свойства компонентов. Эффективный модуль Юнга в направлении волокон. Рассмотрим однонаправленный волокнистый упругий композит с двоякопериодической структурой, компоненты которого идеаль­но связаны между собой. Представительный элемент объема (ячейка периодичности) рассматриваемой гетерогенной среды изображен на рис.4.2. Гетерогенная среда состоит из двух фаз (компонентов): матрицы m и включений (волокон) f. Свойства матрицы m и волокон f приведены в таблице 4.1; объемные концентрации компонентов: .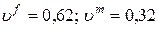

Отметим, что гетерогенная среда двоякопериодической структуры, составленная из ячеек периодичности, изображен­ных на рис.4.2, является макроскопически трансверсально-изотропной средой.

Используя данные таблицы 4.1, определим эффективный модуль Юнга в направлении волокон (3.1.3):

4.2.2. Эффективные модули Юнга и коэффициенты Пуассона. Для конечно-элементного решения задачи (1) о поперечном растяжении ячейки периодичности при задании кинематико-статических условий (3.1.4) используем две конечно-элементные модели:

M–8/64/221 – КЭ-модель 1-го уровня;

М–8/256/825 – КЭ-модель 2-го уровня.

 

 

Рис. 4.2. Представительный элемент объема (ячейка периодичности)

 

В таблице 4.4 представлены основные параметры используемых конечно- элементных моделей и соответствующих им систем конечно-элементных уравнений. На рис.4.3 представлена конечно-элементная модель М–8/256/825 части ячейки периодичности.

Таблица 4.4

---

Дата добавления: 2015-12-17; просмотров: 20; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!