Численное интегрирование
К настоящему времени разработано много различных методов и приёмов численного интегрирования дифференциальных уравнений. Для примера упомянем следующие методы численного интегрирования: Рунге-Кутта, Адамса, Коуэлла, Штермера, Грэгга-Булирша-Штёра, Зверхарта. Различают одношаговые и многошаговые методы численного интегрирования, Если начальные условия интегрирования заданы в одной точке, то это одношаговые методы, Если же начальные условия заданы в виде таблицы, т.е. известны начальные условия в нескольких точках, - одношаговые, а методы Адамса, Коуэлла, Штермера – многошаговые.
Весьма плодотворной оказалась идея применения разложения правых частей дифференциальных уравнений в ряды Тейлора. Реализация этой идеи ведёт к крайней простоте численного решения задачи Коши для обыкновенных дифференциальных уравнений. Рассмотрим сущность этих методов на примере интегрирования дифференциальных уравнений.
Пусть задано дифференциальное уравнение первого порядка (дифференциальное уравнение высокого порядка можно привести к системе уравнений первого порядка):
(4.125)
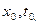- начальные условия интегрирования.
Требуется найти числовые значения х в моменты времени t1, t2,...., tn. Разность t1 - t1-l = H называется шагом интегрирования, который может быть как постоянным так и переменным. Сущность решения в конце шага заключается в следующем. Разлагаем на интервале Н правые части (4.125) в ряд Тейлора по степеням Н (в примере ограничимся членом с третьей производной):
|
|
|
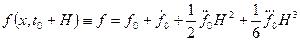(4.126)
В целях сокращения записи здесь использованы обозначения:
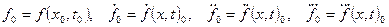(4.127)
Подставив (4.127) в (4.126), дифференциальное уравнение сразу же интегрируется, и решение в конце первого шага получается в виде:
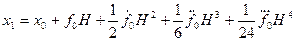(4.128)
Принимая теперь полученное решение в конце первого шага х1, t1 за новые начальные условия, после интегрирования получим х2, t2 и т.д.
Однако в подавляющем большинстве случаев достаточно просто вычислить производные в (4.126) не удаётся - формулы получаются слишком сложные. В этом случае для вычисления производных прибегают кразличным способам аппроксимации, которых достаточно много. В связи с этим понятно происхождение большого количества методов численного интегрирования.
Здесь уместно заметить, что существенной проблемой любых численных методов интегрирования является накопление погрешностей при интегрировании. Погрешность при интегрировании приближенно можно оценить по формуле.
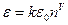
В этой формуле:
0.1 < k < 2,
ε0 - погрешность на одном шаге,
n – количество шагов,
v = 0.5 – для уравнений первого порядка,
v = 1.5 – для уравнений второго порядка.
Дата добавления: 2016-01-05; просмотров: 26; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!