Глава 3. Гидродинамика

 

Гидродинамика – это раздел гидравлики, в котором изучаются движение несжимаемых жидкостей и их взаимодействие с твердыми телами.

Для описания течения жидкостей с применением современного математического аппарата в качестве объекта исследования используют абстрактную, не существующую в природе абсолютно несжимаемую и невязкую жидкость, которую называют идеальной жидкостью. Главное, чем отличается идеальная жидкость от реальной, - это отсутствие у нее вязкости, вызывающей способность сопротивления сдвигу, т.е. возникновению касательных напряжений (трения жидкости).

Основные уравнения, которые позволяют решать задачи о движении идеальной жидкости – уравнение неразрывности (расхода) и уравнение Бернулли.

Исходя из закона сохранения вещества, а также из предположения о сплошности (неразрывности) потока для установившегося течения несжимаемой жидкости, можно утверждать, что величины объемных расходов через любые сечения потока одинаковы (рис. 3.1).

Рис. 3.1. Схема течения жидкости по трубе переменного сечения

 

Это явление описывается уравнением неразрывности (расхода):

(3.1)

Отсюда следует, что

(3.2)

т.е. средние скорости в потоке несжимаемой жидкости обратно пропорционально площадям сечений.

Уравнение неразрывности позволяет определить среднюю скорость в любом сечении потока, например в сечении 2-2, геометрические размеры которого известны (S₂), если известны хотя бы одна средняя скорость потока и площадь его поперечного сечения, например, скорость в сечении 1-1 площадью .

Уравнение Бернулли для потока идеальной жидкости выражает собой закон сохранения энергии жидкости вдоль потока и записывается в виде равенства удельных энергий в двух сечениях. Под удельной понимают энергию, отнесенную к единице веса, объема или массы жидкости. Обычно удобнее бывает относить энергию к единице веса.

Механическая энергия движущейся жидкости может иметь три формы: энергия положения, давления и кинетическая энергия. Первая и третья формы механической энергии известны из механики и в равной степени свойственны твердым и жидким телам. Энергия давления является специфической для движущихся жидкостей. В процессе движения идеальной жидкости одна форма движения может превращаться в другую, однако величина полной энергии жидкости остается неизменной.

Уравнение Бернулли, записанное для сечений 1-1 и 2-2 элементарной струйки или потока идеальной жидкости, имеет вид

(3.3)

где z – геометрическая высота, или геометрический напор (вертикальная координата центров тяжести сечений или удельная энергия положения);

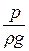- пьезометрическая высота, или пьезометрический напор (удельная энергия давления);

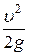- скоростная высота, или скоростной напор (удельная кинетическая энергия);

Н – полный напор, или полная удельная энергия жидкости в сечении.

Очевидно, что для идеальной движущейся жидкости сумма трех высот (напоров): геометрического, пьезометрического и скоростного есть величина постоянная вдоль всего потока (рис.3.2).

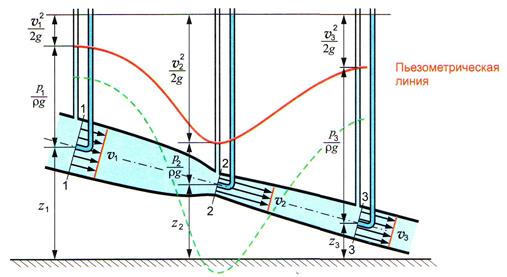
Рис. 3.2. Графическая иллюстрация уравнения Бернулли для потока идеальной жидкости

 

Замер напоров в трех сечениях трубы переменного сечения осуществляется пьезометрами и трубками Пито. Напомним, что пьезометры служат для измерения пьезометрического напора 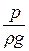. Трубки Пито, представляющие собой изогнутые трубки, отверстия которых расположены перпендикулярно линиям тока жидкости, а противоположные колена ориентированы вертикально, показывают полный, за исключением геометрического, напор, т.е. .

Разность показаний трубок Пито и пьезометров представляют собой скоростной напор 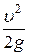в данном сечении.

Линию измерения пьезометрических высот называют пьезометрической линией, ее можно рассматривать как геометрическое место уровней в пьезометрах, установленных вдоль потока.

Штриховой линией на рис.3.2 показана пьезометрическая линия при увеличении расхода жидкости в раз, вследствие чего скоростные высоты увеличиваются в 2 раза, а в узкой части потока давление становится меньше атмосферного.

Если энергию жидкости отнести к единице ее объема, то члены уравнения Бернулли будут иметь размерность давления, а само уравнение (3.3) примет вид, которым также часто пользуются:

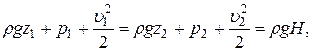
где - весовое давление;

р – гидромеханическое давление (или просто давление).

Если же энергию жидкости отнести к единице массы, можно получить 3-ю формулу записи уравнения (3.3):

.

При течении реальной жидкости между ее слоями возникает трение, что приводит к существенной неравномерности распределения скоростей по сечению потока, а также потерям энергии при перемещении жидкости от одного сечения к другому (рис 3.3).

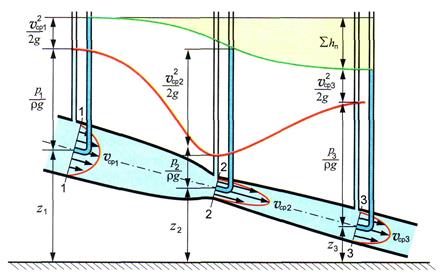
Рис. 3.3. Графическая иллюстрация уравнения Бернулли для потока реальной жидкости

 

Уравнение Бернулли для реальной (вязкой) жидкости следует писать в таком виде:

(3.4)

где - коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечениям потока;

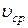- средняя по сечению скорость, равная ;

- суммарные потери полного напора.

Потери энергии при течении жидкости делятся на 2 вида: потери на трение по длине 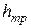и местные потери (рис 3.4).

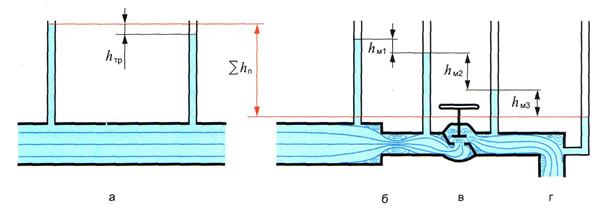
Рис. 3.4. Гидравлические потери по дине (а) и местные (б, в, г)

 

Потери на трение по длине 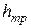- это потери энергии, которые в чистом виде возникают в прямых трубах постоянного сечения, т.е. при равномерном течении, и возрастают пропорционально длине трубы. Данные потери обусловлены не только трением жидкости о стенки канала, но и трением слоев жидкости между собой, а потому имеют место не только в шероховатых, но и в гладких трубах.

Потери на трение по длине имеют достаточно сложную зависимость от средней скорости жидкости и подсчитываются по формуле Дарси-Вейсбаха:

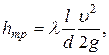(3.5)

или

,

где - это коэффициент Дарси (коэффициент потерь на трение по длине, или коэффициент сопротивления трения);

- длина трубы;

- диаметр трубы.

Значения коэффициента потерь на трение по длине зависит от многих факторов, и в первую очередь от режима течения жидкости.

Для ламинарного режима

(3.6)

Учитывая, что

находим

Полученное выражение отражает закон Пуазейля: при ламинарном режиме течения потеря давления на трение в трубах круглого сечения пропорциональна вязкости и расходу (а, следовательно, и скорости течения) жидкости, в первой степени и обратно пропорциональна диаметру в четвертой степени.

Распределение скоростей по поперечному сечению круглой трубы радиусом r при ламинарном режиме течения выражается параболическим законом:

(3.7)

при чем максимальная скорость на оси трубы в два раза больше средней.

При ламинарном течении в зазоре между двумя плоскими стенками вместо (3.6) используют

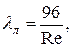(3.8)

где число Рейнольдса .

Формула (3.8) справедлива также для зазора, образованного двумя соосными цилиндрическими поверхностями при условии, что зазор весьма мал по сравнению с диаметром этих поверхностей.

Наличие эксцентриситета этих поверхностей уменьшает потерю напора при том же расходе (или увеличивает расход при том же напоре). При максимальном эксцентриситете (при касании поверхностей) уменьшение напора будет в 2,5 раза.

При ламинарном течении в трубке квадратного сечения вместо (3.6) и (3.8) можно принимать

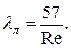(3.9)

Ввиду сложности турбулентного течения и трудности его аналитического исследования, в большинстве случаев для практических расчетов пользуются экспериментальными данными.

Для гидравлически гладких труб (т.е. для труб, в которых шероховатости скрытых в толще ламинарного граничного слоя жидкости у стенок) при можно определять по полуэмпирической формуле Блазиуса:

(3.10)

Для шероховатых труб зависит не только от числа Рейнольдса, но и от шероховатости внутренней поверхности труб (рис. 3.5).

Рис. 3.5. Зависимость от Re и шероховатости труб

Анализируя приведенные зависимости можно отметить следующие три области значений Re и 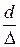, отличающиеся друг от друга характером изменения коэффициента .

Первая область – область малых значений Re и больших значений 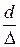, где коэффициент от шероховатости не зависит, а определяется лишь числом Re; это область гидравлически гладких труб.

Во второй области коэффициент зависит одновременно от двух параметров – числа Re и отношения .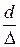

Третья область – область больших Re и малых 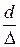, где (при достижении некоторого предельного значения Re_кр) коэффициент не зависит от Re, а определяется лишь отношением 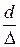. Эту область называют областью автомодельности, или режимом квадратичного сопротивления, так как независимость коэффициента от Re означает, что потеря давления пропорциональна скорости во второй степени.

Для практических расчетов по определению потерь в трубах можно воспользоваться формулой А.Д. Альтшуля:

(3.11)

Характерные значения , мм, для труб из различных материалов приведены ниже (более подробная таблица дана в Приложении 7):

 

стекло……………………………………………………..0

трубы, тянутые из латуни, свинца, меди………………0…0,002

высококачественные бесшовные стальные трубы……0,06…0,2

стальные трубы………………………………………….0,1…0,5

чугунные асфальтированные трубы……………………0,1…0,2

чугунные трубы………………………………………….0,2…1,0

 

К местным потерям напора относят короткие участки трубопроводов, в которых происходит деформация потока, то есть изменение скоростей движения жидкости по величине и/или направлению. Простейшими местными гидравлическими сопротивлениями являются:

- расширение потока;

- сужение потока;

- поворот потока.

Большинство местных сопротивлений, включая гидравлическую арматуру (вентили, краны, задвижки, клапаны), представляет собой комбинации простейших местных сопротивлений.

Местные потери определяются по формуле Вейсбаха:

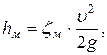(3.12)

или

где 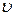- средняя скорость потока в трубе, в которой установлено данное местное сопротивление;

- безразмерный коэффициент местного сопротивления.

Значение зависит от формы местного сопротивления, шероховатости его стенок, условий входа и выхода из него жидкости и основного критерия динамического подобия напорных потоков – числа Рейнольдса.

Число Рейнольдса обычно относят к сечению трубопровода, на котором находится местное сопротивление:

(3.13)

где 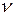- кинематическая вязкость жидкости.

Для некруглых труб

где D_г – гидравлический диаметр, равный отношению площади сечения трубы к ¼ периметра сечения.

Число Рейнольдса определяет режим течения жидкостей (и газов) в трубах.

При Re < Re_кр, где Re_кр ≈ 2300, режим течения ламинарный, т.е. слоистый – без перемешивания жидкости и без пульсаций скоростей и давлений.

При Re > Re_кр режим течения турбулентный, т.е. с перемешиванием жидкости и с пульсациями скоростей и давлений.

Можно считать, что при турбулентном режиме коэффициенты местных сопротивлений от числа Рейнольдса не зависят, следовательно, как видно из формулы (3.12), потеря напора пропорциональна квадрату скорости (квадратичный режим сопротивления). При ламинарном режиме считают, что

(3.14)

где А – число, определяемое формой местного сопротивления;

- коэффициент местного сопротивления на режиме квадратичного сопротивления, т.е. при .

Из-за сложности процессов, происходящих в местных гидравлических сопротивлениях, теоретически найти удается только в отдельных случаях, большинство же значений этого коэффициента получено в результате экспериментальных исследований (рис. 3.6).

 

 

Рис. 3.6. Потери в простейших местных сопротивлениях

 

В гидравлических системах достаточно часто встречаются постепенное сужение потока, называемое конфузором, и постепенное расширение потока, называемое диффузором. Эти местные сопротивления могут иметь достаточно большие длины, поэтому кроме потерь из-за вихреобразования, вызванного изменением геометрии потока, в них учитываются потери давления на трение по длине. Расчет потерь в конфузорах и диффузорах приводится в справочной литературе.

Коэффициенты потерь для прямоугольных тройников представлены на рис. 3.7.

 

Рис. 3.7. Коэффициенты для прямоугольных тройников

 

В случае внезапного расширения трубопровода местная потеря напора при больших числах Рейнольдса выражается формулой Борда:

(3.15)

где и 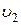- средние скорости в сечениях до и после внезапного расширения соответственно;

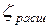- коэффициент сопротивления, равный для данного случая

(3.16)

где S₁ и S₂ – площади сечений трубы до и после внезапного расширения соответственно.

При внезапном сужении трубы без закругления коэффициент сопротивления определяют по формуле Идельчика:

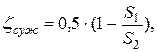(3.17)

где S₁ и S₂ – площади сечений трубы до и после сужения соответственно.

Значение коэффициента сопротивления входа в трубу из большого резервуара зависит от формы входной кромки. В случае острой входной кромки при больших числах Рейнольдса можно принимать .

При выходе потока из трубы в резервуар потеря напора и коэффициент сопротивления выхода равны:

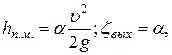
где 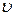- средняя скорость в выходном сечении трубы;

α – коэффициент кинетической энергии (при турбулентном режиме α ≈ 1 и ).

При последовательном расположении в трубопроводе различных местных сопротивлений общая потеря напора в магистрали равна сумме потерь в отдельных ее компонентах. При практических расчетах трубопроводов потерями, вызванными взаимным влиянием друг на друга близко расположенных местных сопротивлений, обычно пренебрегают.

 

---

Дата добавления: 2016-01-05; просмотров: 32; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!