Замена переменной в определенном интеграле
Теорема. Пусть функция 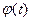 имеет непрерывную производную на отрезке
имеет непрерывную производную на отрезке 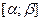 ,
, 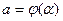 ,
, 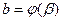 и функция
и функция 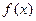 непрерывна в каждой точке
непрерывна в каждой точке 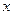 вида
вида 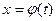 , где
, где 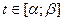 . Тогда справедливо следующее равенство
. Тогда справедливо следующее равенство 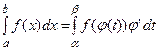 .
.
Пример. Вычислить определенный интеграл 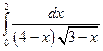 .
.
Пусть 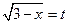 ,
, 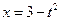 ,
,  ,
, 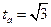 ,
, 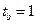 , тогда
, тогда 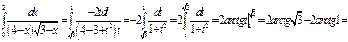
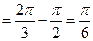 .
.
Вычисление определенного интеграла по частям.
Теорема. Пусть функции 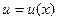 и
и 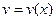 имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке 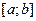 . Тогда
. Тогда 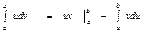 .
.
Пример. Вычислить 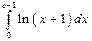 .
.
Пусть  ,
, 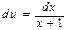 ,
, 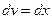 ,
, 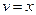 , тогда
, тогда 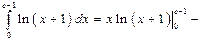
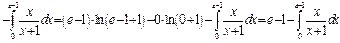 .Вычислим
.Вычислим 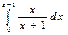 .
. 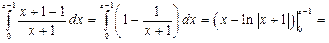
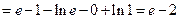 .
.
Итак, 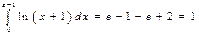 .
.
Интегрирование функций, неопределенных в конечном числе точек.
Определение. Несобственным интегралом 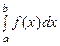 от функции
от функции 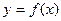 на полуинтервале
на полуинтервале 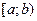 называется предел
называется предел 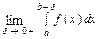 , где
, где 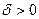 , т.е.
, т.е. 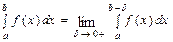 .
.
Пример. Вычислить несобственный интеграл 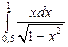 или доказать его расходимость.
или доказать его расходимость.
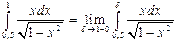 .
.
Вычислим 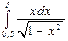 . Пусть
. Пусть 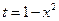 ,
, 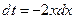 ,
, 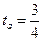 ,
, 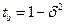 , тогда
, тогда 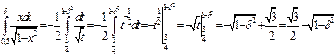
Итак, 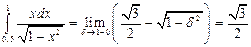 .
.
Интегрирование функций, имеющих разрывы второго рода
Для установления сходимости или расходимости несобственных интегралов с бесконечным верхним пределом интегрирования часто используется следующий признак.
Пусть при 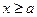 справедливо неравенство
справедливо неравенство 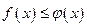 , где
, где 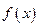 и
и 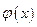 - непрерывные знакоположительные функции. Тогда:
- непрерывные знакоположительные функции. Тогда:
1) если сходимости 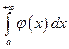 , то сходится
, то сходится 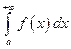 ;
;
2) если расходится 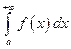 , то расходиться и
, то расходиться и 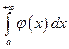 .
.
Аналогичный признак сравнения имеет место и для несобственных интегралов от разрывных функций.
Пример. Вычислить несобственный интеграл или доказать его расходимость: 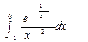 .
.
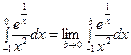 . Пусть
. Пусть  ,
, 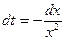 ,
, 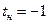 ,
, 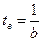 , тогда
, тогда 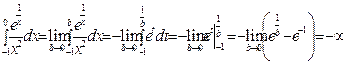 . Несобственный интеграл расходится.
. Несобственный интеграл расходится.
Интегрирование функций, заданных на бесконечном интервале.
|
|
|
Определение. Несобственным интегралом 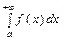 от функции
от функции 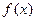 на полуинтервале
на полуинтервале 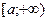 называется предел функции
называется предел функции 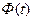 при
при 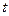 , стремящемся к
, стремящемся к 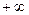 , т.е.
, т.е. 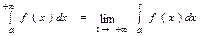 .
.
Пример. Вычислить несобственный интеграл  или доказать его расходимость.
или доказать его расходимость.
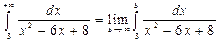 .
.
Вычислим  .
. 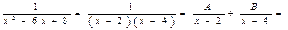
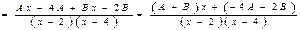 ,
, 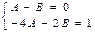 ,
, 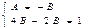 ,
,  ,
, 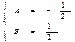 ,
, 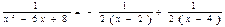 ,
, 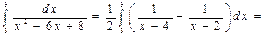

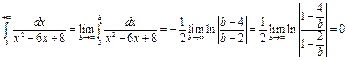 Т. к.интеграл
Т. к.интеграл 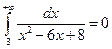 , то он сходится.
, то он сходится.
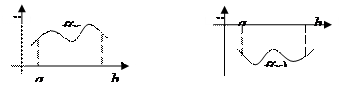
Вычисление площади плоской фигуры.
Вычисление площадей плоских фигур. Рассмотрим несколько случаев вычисления площадей плоских фигур.
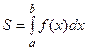
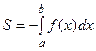
 |

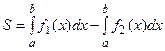
 Пример. Сделать чертеж и вычислить площадь фигуры ограниченной данными линиями
Пример. Сделать чертеж и вычислить площадь фигуры ограниченной данными линиями  ,
, 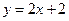 .
.
 |
| 8 | |||||||
| 6 | |||||||
| 4 | |||||||
| 2 | |||||||
 -6 -6
| -4 | -2 | 0 | 2 | 4 | 6 | |
| -2 |
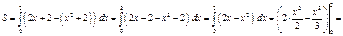
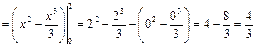 кв. ед.
кв. ед.
Вычисление объема тела вращения.
Объем тела, образованного вращением вокруг оси 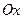 криволинейной трапеции, ограниченной непрерывной кривой
криволинейной трапеции, ограниченной непрерывной кривой 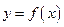 , осью абсцисс и двумя прямыми
, осью абсцисс и двумя прямыми 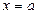 и
и 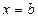
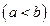 , находится по формуле
, находится по формуле 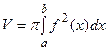 .
.
Пример. Найти объем тела, получающегося при вращении кривой 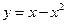 вокруг оси
вокруг оси 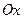 от
от 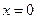 до
до 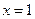 .
. 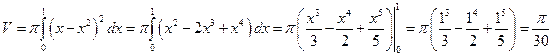 куб. ед.
куб. ед.
|
|
|
Вычисление длины дугиплоской кривой.
Если кривая  на отрезке
на отрезке 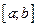 является гладкой (т.е. производная
является гладкой (т.е. производная  - непрерывная функция), то длина дуги этой кривой, заключенной между точками с абсциссами
- непрерывная функция), то длина дуги этой кривой, заключенной между точками с абсциссами 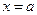 и
и 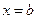
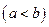 , находится по формуле
, находится по формуле  .
.
Пример. Найти длину дуги кривой 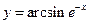 от
от 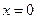 до
до 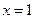 .
.
Так как 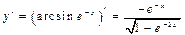 ,
, 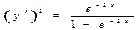 то
то 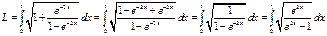 . Пусть
. Пусть 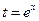 ,
, 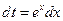 ,
, 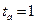 ,
, 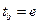 , тогда
, тогда 
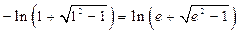 .
.
Пример. Найти длину дуги кривой 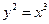 между точками
между точками 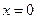 и
и 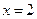 в первой четверти.
в первой четверти.
Длину дуги кривой определим по формуле 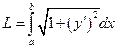 .Т. к.
.Т. к. 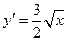 ,
, 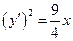 , то
, то 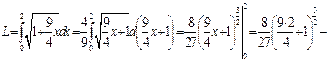
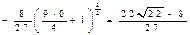 .
.
Вычисление площади поверхности тела вращения.
Площадь поверхности, образованной вращением оси 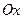 дуги гладкой кривой
дуги гладкой кривой 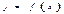 между точками
между точками 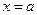 и
и 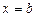
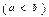 , находится по формуле
, находится по формуле  .
.
Пример. Найти площадь поверхности вращения вокруг оси 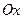 дуги кубической параболы
дуги кубической параболы 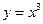 при
при  .
.
Так как 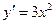 , то
, то 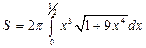 . Пусть
. Пусть 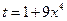 ,
,  ,
, 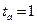 ,
, 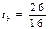 , тогда
, тогда 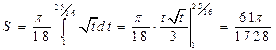 .
.
Дата добавления: 2020-04-25; просмотров: 84; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
