Определенный интеграл и его геометрический смысл.
Пусть функция  неотрицательна на
неотрицательна на 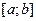 . Отдельное слагаемое
. Отдельное слагаемое  интегральной суммы
интегральной суммы  в этом случае равно площади
в этом случае равно площади 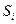 прямоугольника со сторонами
прямоугольника со сторонами 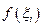 и
и 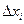 , Другими словами,
, Другими словами, 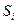
 - это площадь под прямой
- это площадь под прямой  на отрезке
на отрезке  . Поэтому вся интегральная сумма
. Поэтому вся интегральная сумма  равна площади
равна площади  под ломаной, образованной на каждом из отрезков
под ломаной, образованной на каждом из отрезков  прямой
прямой  , параллельной оси абсцисс.
, параллельной оси абсцисс.
Определение. Пусть предел интегральной суммы 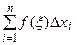 при стремлении
при стремлении 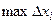 к нулю существует, конечен и не зависит от способа выбора точек
к нулю существует, конечен и не зависит от способа выбора точек 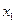 ,
, 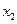 , … и точек
, … и точек 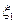 ,
, 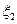 , ... Тогда этот предел называется определенным интегралом от функции
, ... Тогда этот предел называется определенным интегралом от функции  на
на 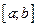 , обозначается
, обозначается  , а сама функция
, а сама функция  называется интегрируемой на отрезке
называется интегрируемой на отрезке 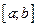 , т.е.
, т.е. 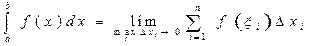 .
.
Геометрический смысл определенного интеграла. Определенный интеграл численно равен площади криволинейной трапеции.
Основные свойства определенного интеграла.
1. Постоянный множитель можно выносить за знак интеграла, т.е.  .
.
2. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.  .
.
3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е. 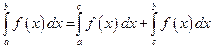 .
.
Основные условия интегрируемости функций.
Теорема. Если функция  непрерывна на отрезке
непрерывна на отрезке 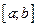 , то она интегрируема на этом отрезке.
, то она интегрируема на этом отрезке.
Пример. Вычислить 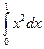 .
.
Запишем выражение для интегральной суммы, предполагая, что все отрезки 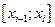 разбиения имеют одинаковую длину
разбиения имеют одинаковую длину 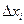 , равную
, равную 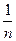 , где
, где 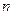 - число отрезков разбиения, причем для каждого отрезка
- число отрезков разбиения, причем для каждого отрезка 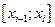 разбиения точка
разбиения точка  совпадает с правым концом этого отрезка, т.е.
совпадает с правым концом этого отрезка, т.е.  , где
, где 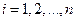 . В силу интегрируемости функции
. В силу интегрируемости функции  , выбор такого «специального» способа разбиения отрезка интегрирования на части и точек
, выбор такого «специального» способа разбиения отрезка интегрирования на части и точек  на отрезке разбиения не повлияет на искомый предел интегральной суммы. Тогда
на отрезке разбиения не повлияет на искомый предел интегральной суммы. Тогда 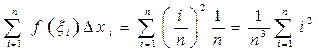 .
.
|
|
|
Известно, что сумма квадратов чисел натурального ряда равна 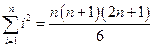 . Следовательно,
. Следовательно, 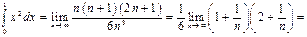
 .
.
Связь определенного интеграла с первообразной. Формула Ньютона-Лейбница
Теорема. Если функция  непрерывна на отрезке
непрерывна на отрезке  , то найдется такое значение
, то найдется такое значение  , что
, что 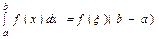 .
.
Доказательство. По свойству функции, непрерывной на отрезке, для произвольного значения 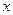 из
из 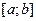 верно, что
верно, что 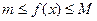 , где
, где 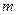 и
и 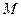 - наименьшее и наибольшее значения функции на
- наименьшее и наибольшее значения функции на 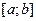 . Тогда, имеем
. Тогда, имеем 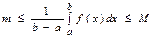 .
.
Но функция, непрерывная на отрезке, принимает любое значение, заключенное между наименьшим и наибольшим значениями. Поэтому, в частности, найдется такое число  , что
, что 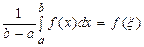 или
или 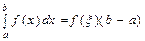 .
.
Теорема. Пусть функция 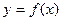 непрерывна на отрезке
непрерывна на отрезке 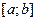 и
и  - любая первообразная для
- любая первообразная для 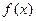 на
на 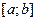 . Тогда определенный интеграл от функции
. Тогда определенный интеграл от функции 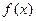 на
на 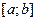 равен приращению первообразной
равен приращению первообразной  на этом отрезке, т.е.
на этом отрезке, т.е. 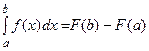 .
.
Доказательство. Пусть  - некоторая первообразная для функции
- некоторая первообразная для функции 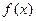 . По теореме (если функция
. По теореме (если функция 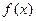 непрерывна на отрезке
непрерывна на отрезке 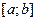 , тогда в каждой точке
, тогда в каждой точке 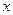 отрезка
отрезка 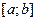 производная функции
производная функции  по переменному верхнему пределу равна подынтегральной функции
по переменному верхнему пределу равна подынтегральной функции 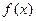 ), т.е.
), т.е. 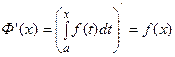 функция
функция  , заданная формулой
, заданная формулой  , также является первообразной для функции
, также является первообразной для функции 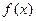 .
.
|
|
|
По теореме: если 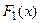 и
и 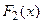 - первообразные для функции
- первообразные для функции 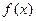 на промежутке
на промежутке  , то найдется такое число
, то найдется такое число 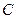 , что будет справедливо равенство
, что будет справедливо равенство 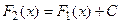 ) найдется такое число
) найдется такое число 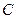 , что
, что 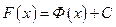 .
.
Тогда для приращения первообразной имеем 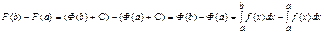 . Так как
. Так как  , то
, то 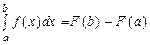 .
.
Пример. Вычислить 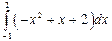 .
.
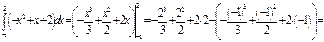
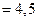 .
.
Дата добавления: 2020-04-25; просмотров: 119; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
