Интегрирование способом подстановки.
Экстремумы функции нескольких переменных. Понятие о векторе градиента функции двух переменных.
Определение. Точка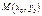 
называется точкой макс (минимума) функции 
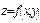, если существует окрестность точки 
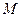, такая, что для всех 
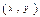из этой окрестности выполняется неравенство 
, 
.
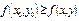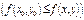Теорема.Пусть точка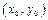 
- есть точка экстремума дифференцируемой функции 
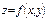. Тогда частные производные 
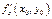и 
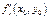в этой точке равны нулю.
Теорема.Пусть функция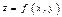 
: а) определена в некоторой окрестности критической точки 
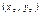, в которой 
и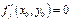 
; б) имеет в этой точке непрерывные частные производные второго порядка
Определение. Производной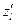 
по направлению 
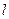функции двух переменных 
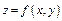называется предел отношения приращения функции в этом направлении к величине перемещения 
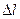при стремлении последней к нулю, т.е. 
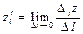Определение.Градиентом 
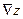функции 
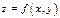называется вектор с координатами 
.
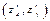Теорема. Пусть задана дифференцируемая функция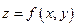 
и пусть в точке 
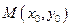, величина градиента отлична от нуля. Тогда градиент перпендикулярен линии уровня, проходящей через данную точку.
Пример. Найти критические (экстремальные) точки функции двух переменных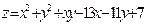 
.
Найдем частные производные функции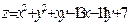 
: 
, 
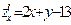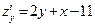. Найдем критические точки функции из системы уравнений 
, 
, 
, 
, 
, 
, 
, 
.
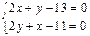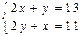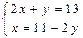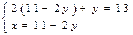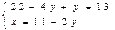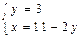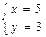Найдем частные производные второго порядка: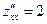 
, 
, 
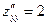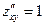. Проверим выполнение достаточного условия экстремума: 
. Так как 
, 
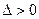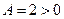, то точка 
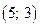есть точка минимума.
Пример.Для функции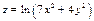 
в точке 
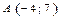найти градиент и производную по направлению 
.
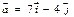Найдем частные производные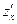 
, 
: 
, 
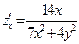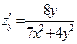. Значения частных производных в точке 
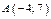равны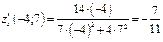 
, 
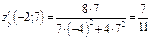. Градиент функции 
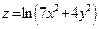в точке 
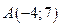равен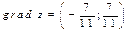 
.
Так как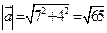 
, то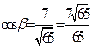 
, 
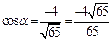, то производная по направлению 
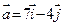равна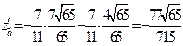 
.
Понятие первообразной, основные свойства.
Определение. Функция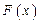 
называется первообразной функцией для функции 
на промежутке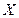 
, если в каждой точке 
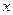этого промежутка 
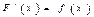.Например, 
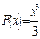является первообразной для функции 
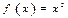, так как 
.
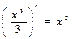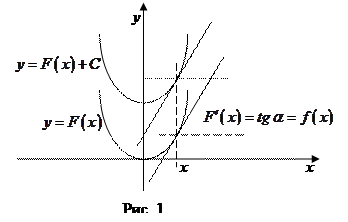
По геометрическому смыслу производной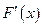 
есть угловой коэффициент касательно к кривой 
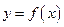в
точке с абсциссой 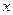. Геометрически найти первообразную для 
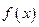- значит найти такую кривую 
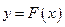, что угловой коэффициент касательной к ней в произвольной точке 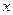равен значению 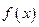заданной функции в этой точке (рис. 1).
Следует отметить, что для заданной функции 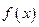ее первообразная определена неоднозначно. Дифференцируя, нетрудно убедиться, что функции 
, 
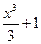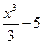и вообще 
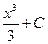, где 
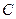- некоторое число, являются первообразными для функции 
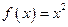. Аналогично в общем случае, если 
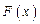- некоторая первообразная для 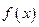, то поскольку 
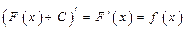, функции вида 
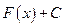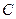, где - произвольное число, также являются первообразными для .
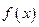Геометрически это означает, что если найдена одна кривая 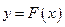, удовлетворяющая условию 
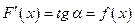, то, сдвигая ее вдоль оси ординат, мы вновь получаем кривые, удовлетворяющие указанному условию (поскольку такой сдвиг не меняет углового коэффициента касательной в точке с абсциссой 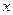) (рис. 1).
Остается вопрос, описывает ли выражение вида 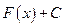все первообразные для функции 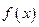. Ответ на него дает следующая теорема.
Теорема. Если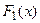 
и 
- первообразные для функции 
на промежутке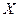 
, то найдется такое число 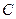, что будет справедливо равенство 
.
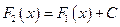Поскольку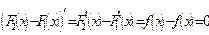 
, то по следствию из теоремы Лагранжа, найдется такое числ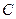о , что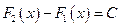 
или .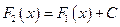
Из данной теоремы следует, что если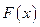 
- первообразная для функции 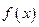, то выражение вида 
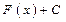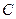, где - произвольное число, задает все возможные первообразные для .
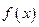Определение. Совокупность всех первообразных для функции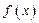 
на промежутке 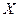называется неопределенным интегралом от функции 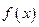и обозначается 
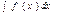, где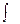 
- знак интеграла, 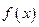- подынтегральная функция,
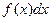- подынтегральное выражение. Таким образом 
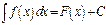, где 
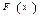- некоторая первообразная для 
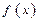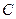, - произвольное постоянна
Отметит, что в определении неопределенного интеграла не исключается, что 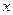сама, возможно, является функцией некоторой переменной, однако при проверке правильности нахождения первообразной это несущественно, так как дифференцировать следует лишь по переменной .
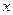Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции.
Свойства неопределенного интеграла:
1. Производная от неопределенного интеграла равна подынтегральной функции, т.е.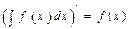 
.
Дифференцируя левую и правую части равенства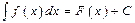 
, получаем 
.
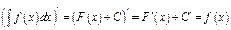2. Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е.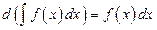 
.
По определению дифференциала и свойству 1 имеем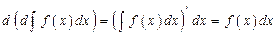 
.
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.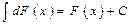 
.
Рассматривая функцию 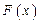как первообразную для некоторой функции 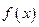, можно записать 
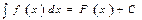и на основании 
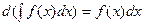дифференциал неопределенного интеграл 
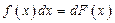, откуда 
.
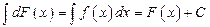Сравнивая между собой свойства 2 и 3, можно сказать, что операции нахождения неопределенного интеграла и дифференциала взаимнообратны (знак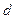и 
и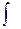 
взаимно уничтожают друг друга, в случае свойства 3, правда, с точностью до постоянного слагаемого).
4. Постоянный множитель можно выносить за знак интеграла, т.е.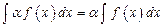 
.
5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.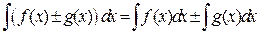 
.
Интегрирование способом подстановки.
Метод замены переменной описывается формулой: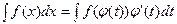 
, где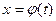 
- функция, дифференцируемая на рассматриваемом промежутке.
Пример. Вычислить неопределенный интеграл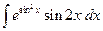 
.
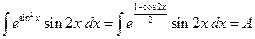. Пусть 
, 
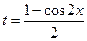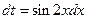, тогда 
.
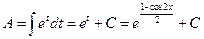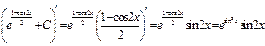
Дата добавления: 2020-04-25; просмотров: 97; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!