Логарифмические уравнения и неравенства
Логарифмом числа b по основанию a называется показатель степени с, в которую нужно возвести основание а, чтобы получить число b: 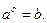 Обозначается
Обозначается 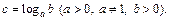
Логарифмическая функция имеет вид  где
где 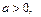
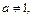
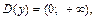
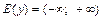 . При
. При  функция убывает, а при
функция убывает, а при 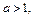 – возрастает.
– возрастает.
При решении логарифмических уравнений и неравенств используются формулы:
1) 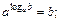 2)
2) 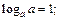 3)
3) 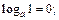
4) 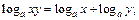 5)
5) 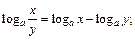
6) 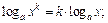 7)
7) 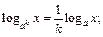
8) 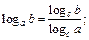 9)
9)  10)
10) 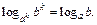
Пример 1. Решить уравнение 
Решение. Из определения логарифма 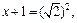 т.е. х=1. Так как областью определения является множество таких значений х, что
т.е. х=1. Так как областью определения является множество таких значений х, что 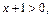 т.е.
т.е.  то х=1 принадлежит области определения и является корнем данного уравнения.
то х=1 принадлежит области определения и является корнем данного уравнения.
Ответ: 1.
Пример 2. Решить уравнение 
Решение. Областью определения данного уравнения является множество значений , удовлетворяющих системе неравенств 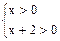 , или
, или  . Используя свойства логарифмов, данное уравнение можно записать как
. Используя свойства логарифмов, данное уравнение можно записать как 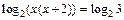 или
или 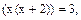 т.е. имеем квадратное уравнение
т.е. имеем квадратное уравнение 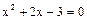 , корнями которого являются
, корнями которого являются 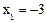 ,
, 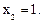 Первый корень не входит в область определения, поэтому не является решением исходного уравнения. Ответ: 1.
Первый корень не входит в область определения, поэтому не является решением исходного уравнения. Ответ: 1.
Пример 3. Решить уравнение 
Решение. Областью определения уравнения является множество значений x>0. Пусть  Тогда
Тогда 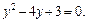 Корнями этого уравнения являются
Корнями этого уравнения являются 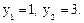 Тогда
Тогда  х=3 и
х=3 и  х=27. Полученные значения х=3 и х=27 принадлежат области определения и являются корнями исходного уравнения.
х=27. Полученные значения х=3 и х=27 принадлежат области определения и являются корнями исходного уравнения.
|
|
|
Ответ; 3; 27.
При решении логарифмических неравенств следует использовать свойства логарифмической функции.
Если 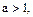 то неравенство
то неравенство 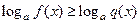 (
( 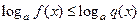 ) равносильно системе неравенств
) равносильно системе неравенств
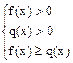
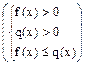 .
.
Если же 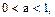 то данное неравенство равносильно системе
то данное неравенство равносильно системе

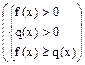 .
.
Пример 4. Найти наибольшее целое решение неравенства 
Решение. Данное неравенство равносильно системе  или
или 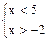 , т.е.
, т.е. 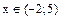 . Наибольшим целым решением является
. Наибольшим целым решением является 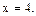 Ответ: 4.
Ответ: 4.
Пример 5. Найти целые решения неравенства 
Решение. Используя свойства логарифмов, данное неравенство можно записать в виде 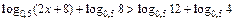 или
или 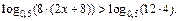 Полученное неравенство равносильно системе
Полученное неравенство равносильно системе 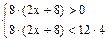 , или
, или 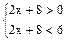 , или
, или 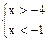 , т.е.
, т.е. 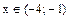 . Целыми решениями исходного неравенства являются числа –3, –2.
. Целыми решениями исходного неравенства являются числа –3, –2.
Ответ: –3, –2.
Пример 6. Решить неравенство 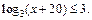
Решение. Запишем неравенство в виде 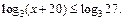 Это неравенство равносильно системе
Это неравенство равносильно системе  или
или  , т.е.
, т.е. 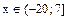 .
.
Ответ:  .
.
Пример 7. Решить неравенство 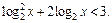
Решение. По определению логарифма 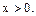 Пусть
Пусть  Тогда
Тогда 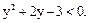 Корнями соответствующего квадратного уравнения являются
Корнями соответствующего квадратного уравнения являются 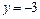 и
и 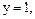 а решениями неравенства являются все значения
а решениями неравенства являются все значения 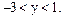 Следовательно,
Следовательно, 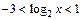 или
или 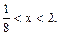
|
|
|
Так как 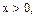 то решениями исходного неравенства являются все значения
то решениями исходного неравенства являются все значения 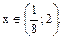 Ответ:
Ответ: 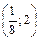 .
.
Упражнения
Решить уравнения.
1.  Ответ: –4.
Ответ: –4.
2. 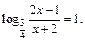 Ответ: 2.
Ответ: 2.
3. 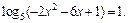 Ответ: –2; –1.
Ответ: –2; –1.
4.  Ответ: 0,5; 16.
Ответ: 0,5; 16.
5. Найти наибольшее целое решение неравенства 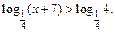
Ответ: –4.
6. Найти целые решения неравенства  Ответ: 0; 1; 2.
Ответ: 0; 1; 2.
7. Решить неравенство 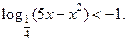 Ответ: (1; 4).
Ответ: (1; 4).
8. Решить неравенство 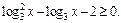
Ответ:  .
.
Тригонометрические преобразования и уравнения
Любые тригонометрические преобразования базируются, прежде всего, на знании тригонометрических формул. В большинстве справочников по математике имеется перечень таких формул, однако запомнить нужно лишь основные, так как остальные являются их следствиями. Поэтому здесь приведены только основные формулы тригонометрии.
|
|
|
Соотношения между тригонометрическими функциями одного и того же аргумента:
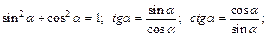
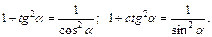
Формулы сложения аргументов:
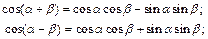
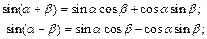
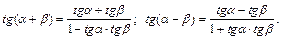
Формулы двойного аргумента:
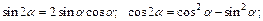
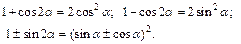
Формулы половинного аргумента:
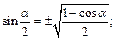
 ;
;

Формулы сложения одноименных тригонометрических функций:


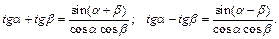
Формулы преобразования произведения в сумму:
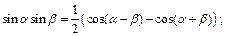
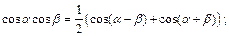
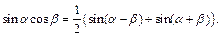
Выражение тригонометрических функций через тангенс половинного угла:
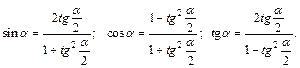
Тригонометрические уравнения путем преобразований с помощью основных формул сводятся к одному из стандартных уравнений, которые достаточно легко решаются:
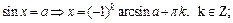
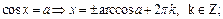

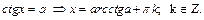
Пример 1. Вычислить 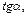 если
если  .
.
Решение. Так как 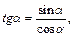 то нужно найти
то нужно найти  . Из основного тригонометрического тождества
. Из основного тригонометрического тождества 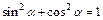 находим
находим 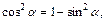
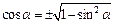 . По условию угол a находится во второй четверти, где
. По условию угол a находится во второй четверти, где  Поэтому
Поэтому 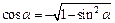 ,
, 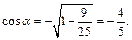 Отсюда
Отсюда 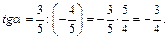
Ответ: 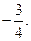
Пример 2. Упростить выражение 
Решение 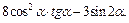 =
= 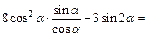
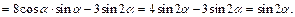
Ответ: 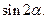
Пример 3. Решить уравнение 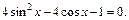
Решение Так как  то данное уравнение примет вид
то данное уравнение примет вид 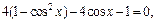
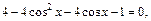
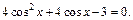
Пусть 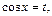 где
где 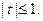 Тогда имеем квадратное уравнение
Тогда имеем квадратное уравнение 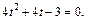 Корнями этого уравнения являются
Корнями этого уравнения являются 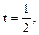
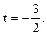 Второй корень не подходит, так как
Второй корень не подходит, так как  Поэтому
Поэтому 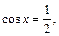
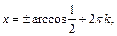
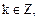 т.е.
т.е. 
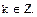
Ответ: 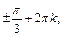
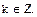
|
|
|
Пример 4. Решить уравнение 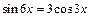 .
.
Решение Используя формулу двойного аргумента 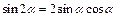 , данное уравнение можно записать в виде
, данное уравнение можно записать в виде 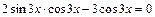 , или
, или 
Следовательно, 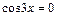 или
или  Из первого уравнения находим
Из первого уравнения находим 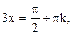
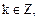 или
или 
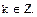 Второе уравнение не имеет решений, так как
Второе уравнение не имеет решений, так как 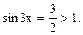
Ответ: 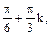

Упражнения
1. Вычислить 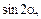 если
если 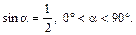 Ответ:
Ответ: 
2. Вычислить значение функции 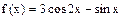 при
при 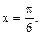
Ответ: 1.
Решить уравнения
3.  Ответ:
Ответ: 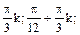
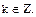
4. 3 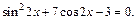
Ответ: 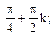

5. 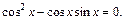
Ответ: 
Дата добавления: 2020-04-08; просмотров: 133; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
