Уравнения и неравенства, содержащие неизвестные
Под знаком абсолютной величины
Наиболее распространенным методом решения уравнений и неравенств, содержащих модули, является метод интервалов, при котором знак модуля раскрывается по определению:


Применение метода состоит в следующем:
1) Находят значения переменной, при которых выражения под знаком модуля обращаются в нуль;
2) Разбивают область допустимых значений переменной на интервалы, на каждом из которых выражения под знаком модуля сохраняют знак;
3) На каждом интервале решают уравнение или неравенство.
Совокупность (объединение) решений из указанных интервалов и составляет все решения исходного уравнения или неравенства.
Пример 1. Решить уравнение 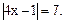
Решение. Найдём нуль модуля: 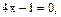
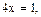
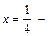 нуль модуля.
нуль модуля.
1) Если  , т.е.
, т.е. 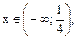 то –
то – 
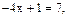
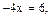
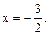
Так как  принадлежит рассматриваемому интервалу, то
принадлежит рассматриваемому интервалу, то  является корнем данного уравнения.
является корнем данного уравнения.
2) Если 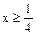 , т.е.
, т.е. 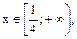
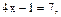 то
то 
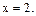
Так как 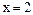 принадлежит рассматриваемому интервалу, то
принадлежит рассматриваемому интервалу, то 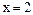 тоже является корнем данного уравнения.
тоже является корнем данного уравнения.
Ответ: 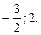
Пример 2. Решить уравнение 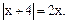
Решение. 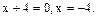 Рассмотрим решение данного уравнения на каждом из двух интервалов.
Рассмотрим решение данного уравнения на каждом из двух интервалов.
1) 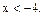 На этом интервале
На этом интервале  Поэтому уравнение имеет вид:
Поэтому уравнение имеет вид: 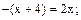
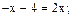
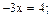
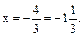
Найденное значение не входит в рассматриваемый интервал.
2) 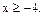 Здесь
Здесь 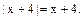 Следовательно,
Следовательно, 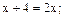

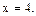 Полученное значение входит в рассматриваемый интервал.
Полученное значение входит в рассматриваемый интервал.
Таким образом, решением исходного уравнения является 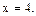
Ответ: 4.
Пример 3. Решить неравенство 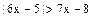 и в ответ записать его наибольшее целое решение.
и в ответ записать его наибольшее целое решение.
|
|
|
Решение. Находим нуль модуля: 
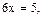
 .
.
Рассмотрим два случая.
1) Если 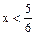 , то
, то 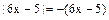 и неравенство примет вид
и неравенство примет вид 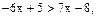 или
или 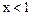 . Следовательно,
. Следовательно, 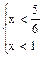 , откуда
, откуда  , т.е.
, т.е.  .
.
2) Если 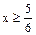 , то
, то  . Тогда
. Тогда 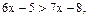 или
или 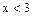 . Следовательно,
. Следовательно, 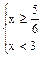 , т.е.
, т.е. 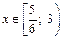 .
.
Объединяя оба случая, получим решение данного неравенства 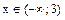 . Наибольшим целым его решением будет
. Наибольшим целым его решением будет 
Ответ: 2.
Пример 4. Решить неравенство 
Решение. Находим нуль модуля: 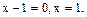
Раскроем модуль на каждом из двух интервалов.
1) 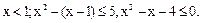 Корни соответствующего квадратного уравнения равны
Корни соответствующего квадратного уравнения равны 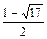 и
и 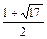 . Решаем квадратное неравенство и с учётом рассматриваемого интервала находим решение:
. Решаем квадратное неравенство и с учётом рассматриваемого интервала находим решение: 
2)  Корни соответствующего квадратного уравнения –3 и 2. Решаем квадратное неравенство, и, учитывая рассматриваемый интервал, находим решение
Корни соответствующего квадратного уравнения –3 и 2. Решаем квадратное неравенство, и, учитывая рассматриваемый интервал, находим решение 
Объединяя оба случая, получаем решение исходного неравенства: 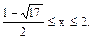
Ответ: 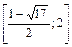 .
.
Упражнения
Решить уравнения.
1.  Ответ:
Ответ: 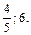
2.  Ответ:
Ответ: 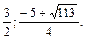
3. 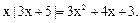 Ответ: 3.
Ответ: 3.
4.  Ответ:
Ответ: 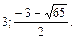
Решить неравенства.
|
|
|
5.  Ответ: (8; 12).
Ответ: (8; 12).
6.  Ответ:
Ответ: 
7. 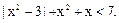 Ответ:
Ответ: 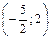
8. Найти наибольшее целое решение неравенства 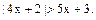
Ответ: –1.
Показательные уравнения и неравенства
При решении показательных уравнений и неравенств необходимо понимать и знать определение и свойства показательной функции.
Показательной называется функция вида 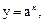 где
где 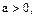

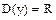 ,
, 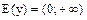 . Если
. Если  то функция возрастает, если
то функция возрастает, если 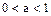 , то убывает. При преобразовании показательной функции необходимо знать правила действий со степенями:
, то убывает. При преобразовании показательной функции необходимо знать правила действий со степенями:
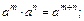
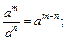
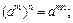
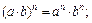
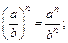

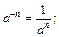

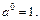
Пример 1. Решить уравнение 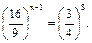
Решение. Так как 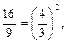
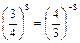 , то данное уравнение запишем в виде
, то данное уравнение запишем в виде 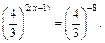 Отсюда
Отсюда
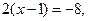
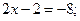

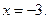
Ответ: 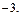
Пример 2. Решить уравнение 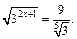
Решение. Запишем уравнение в виде 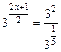 , или
, или 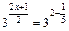 , или
, или 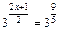 . Отсюда
. Отсюда  , т.е.
, т.е. 
Ответ 
Пример 3. Решить уравнение 
Решение. Имеем  откуда
откуда 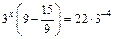 или
или 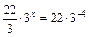 , или
, или 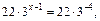 т.е.
т.е. 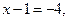
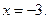
Ответ: 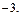
Пример 4. Решить уравнение 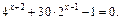
Решение. Запишем уравнение в виде 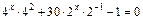 или
или 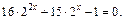
Пусть 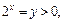 тогда
тогда 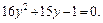
Корнями этого уравнения являются 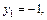
 Первый корень не подходит, так как по условию
Первый корень не подходит, так как по условию 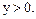 Поэтому
Поэтому 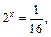
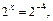 т.е.
т.е. 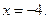
|
|
|
Ответ:  .
.
Решение показательных неравенств основано на свойстве: если  то
то 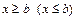 при
при 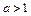 и
и  при
при 
Пример 5. Найти наибольшее целое решение неравенства 
Решение. Так как 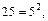 то неравенство можно записать в виде
то неравенство можно записать в виде 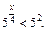 Отсюда
Отсюда 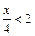 , т.е.
, т.е. 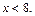 Наибольшим целым числом, удовлетворяющим неравенству, является 7.
Наибольшим целым числом, удовлетворяющим неравенству, является 7.
Ответ: 7.
Пример 6. Решить неравенство 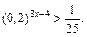
Решение. Запишем неравенство в виде 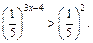 Так как
Так как  то
то 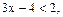
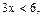
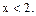
Ответ: 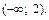
Пример 7. Найти количество целых решений неравенства 
Решение. Перепишем неравенство в виде 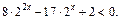 Пусть
Пусть 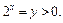 Тогда
Тогда 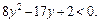 Решая соответствующее квадратное уравнение, получим
Решая соответствующее квадратное уравнение, получим 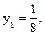
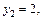 т.е.
т.е. 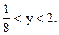 Таким образом,
Таким образом, 
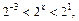 т.е.
т.е. 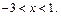 Целыми решениями неравенства являются числа –2, –1, 0 и их количество равно 3.
Целыми решениями неравенства являются числа –2, –1, 0 и их количество равно 3.
Ответ: 3.
Упражнения
Решить уравнения и неравенства.
1. 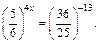 Ответ: 6,5.
Ответ: 6,5.
2. 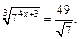 Ответ: 0,375.
Ответ: 0,375.
3. 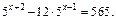 Ответ: 2.
Ответ: 2.
|
|
|
4. 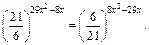 Ответ: 0; 1.
Ответ: 0; 1.
5. 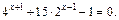 Ответ: –3.
Ответ: –3.
6. Найти наименьшее целое решение неравенства 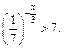
Ответ: 4.
7. Найти наибольшее целое решение неравенства 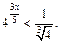
Ответ: –1.
8. Решить неравенство 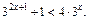 Ответ: (–1; 0).
Ответ: (–1; 0).
9. Решить неравенство  Ответ: (0; 0,4).
Ответ: (0; 0,4).
Дата добавления: 2020-04-08; просмотров: 102; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
