Теорема о биссектрисе угла треугольника
Построим произвольный треугольник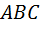 
и проведем в нем биссектрису 
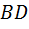(рис. 16). Очевидно, и совсем не удивительно, что биссектриса делит сторону 
треугольника на две неравные части, бо́льшую и меньшую. Определенный интерес вызывает следующее наблюдение: к большей части основания прилегает бо́льшая сторона треугольника. Такое положение имеет место для любых треугольников всевозможных форм и размеров, так что наблюдение школьников отражает, по-видимому, некую качественную закономерность. Однако настоящий интерес вызывает количественная сторона ситуации.
Сформулируем наш «дежурный» вопрос о пропорции применительно к однотипным неравным отрезкам. Во сколько раз бо́льшая часть основания превосходит меньшую часть? Во сколько раз бо́льшая из двух других сторон треугольника превосходит меньшую? Вычислив в интерактивной математической среде необходимые отношения, мы получим, что они равны! (Применительно к рис. 16
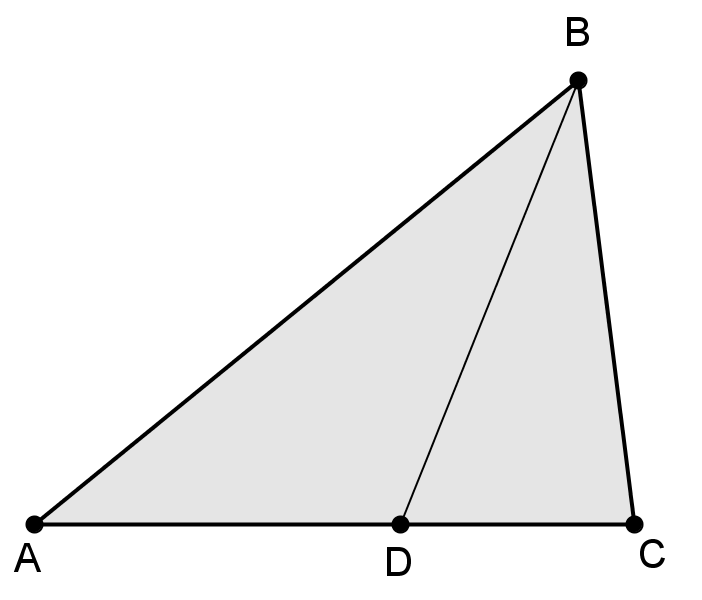Рис. 16. К большей части основания прилегает бо́льшая сторона
.) Равенство отношений имеет место для любых треугольников всевозможных форм и размеров. Оно выполнятся как при стандартной настройке округления до двух разрядов, так и при более тонких настройках до трёх, четырёх, …, десяти разрядов. Этот эксперимент даёт веские основания для следующей гипотезы: биссектриса угла треугольника делит противолежащую сторону на два отрезка, пропорциональные прилежащим сторонам. Так может происходить эмпирическое обнаружение теоремы.
|
|
|
К сожалению, существует одно обстоятельство, которое делает наш эксперимент не вполне убедительным: при настройке округления до 15 разрядов существуют треугольники, для которых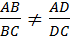 
. Их совсем не трудно обнаружить, двигая вершины с помощью инструмента Перемещать. Получается, что однотипные эксперименты, осуществляемые с разной точностью, дают различные результаты. Разрешить это противоречие с помощью других экспериментов представляется затруднительным или невозможным, поскольку предел точности, предоставляемый компьютером, уже достигнут. В этих условиях единственным средством для снятия противоречия между двумя экспериментами является дедуктивное доказательство.
Приведём готовый чертёж (рис. 17) и систему вопросов, с помощью которых доказательство теоремы может быть получено школьниками в высокой степени самостоятельно. Мы надеемся, что читатель сочтёт предполагаемые ответы учеников весьма вероятными.
В-1. Какие геометрические фигуры изображены на рис. 17?
О-1. Треугольник .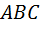
В-2. Ответ правильный, но малополезный, потому что на рисунке изображено много треугольинков. Мы поговорим о них, а пока скажите, какя фигура в определенном смысле уникальна?
|
|
|
О-2. Угол .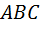
В-3. Как расположен луч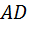 
относительно сторон угла? (Наш «дежурный» вопрос!)
О-3. Он является биссектрисой.
В-4. Есть ли среди многочисленных треугольников подобные?
О-4. Да. Например,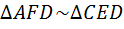 
В-5. А почему?
О-5. Два угла равны, потому что вертикальны, а два других угла являются прямыми по построению.
В-6. Верно. Запишите факт подобия в виде равенств.
О-6.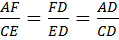 
.
В-7. А есть ли еще пара подобных треугольников? Если да, то почему вы так решили?
О-7. Да, есть. 
, потому что два угла являются прямыми по построению, а два других угла равны, поскольку образо ваны биссектирсой и стороной угла.
В-8. Верно. Запишите факт подобия в виде равенств.
О-8. 
.
В-9. Имеются ли пропорциях Ответов 6 и 8 одинаковые ототношения?
О-9. Да. Это отношение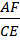 
.
В-10. Объедините все равенства Ответов 6 и 8 в одну серию.
О-10. Получится, что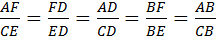 
.
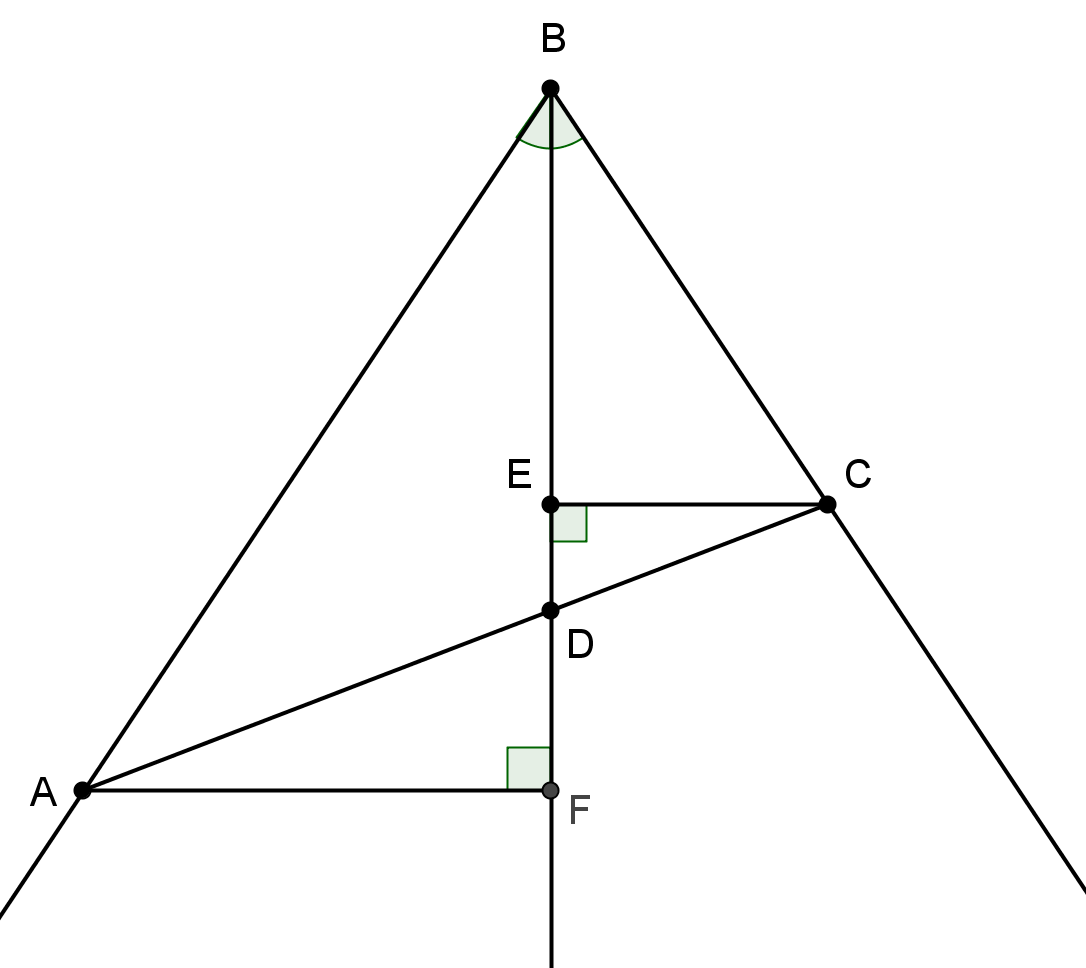
В-11. А теперь самое интересное! Удалите с рис. 17 все элементы, которые не принадлежат треугольнику 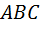. В соотвествии с этим, в равенствах Ответа 10 удалите те отношения, в которых есть обозначения точек, удаленных с чертежа. Что случится с чертежом и с серией равенств?
Рис. 17. Свойство биссектрисы угла треугольника
|
|
|
О-11. С чертежа придется удалить отрезок 
(за исключением точки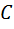 
) и отрезок 
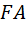(за исключением точки 
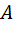). Кроме того, придется заменить луч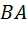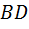и 
, и 
отрезкам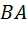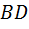и , и соответственно. В результате рис. 17 превратится в рис. 16.
Из формул Ответа 10 придется удалить те отношения, в которых участвуют быквы 
и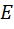 
, то есть придется удалить первое, второе и четвертое отношения. В результате останется формула 
.
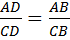В-12. Связан ли полученный результат с той гипотезой, которая возникла в результате эксперимента?
О-12. Да, связан. Наш анализ рис. 17 показывает, что гипотеза оказалась справедливой.
В-13. Можно ли теперь считать, что она является теоремой? Можно ли было считать ее теоремой раньше, до того, как мы провели анализ рис. 17?
О-13. Да, теперь ее можно считаь теоремой. Раньше этого было сделать нельзя, потому что эксперимент при округлении до 15 разрядов противоречил ей.
Обсудим некоторые особенности приведенного сценария, которые важны по тем или иным причинам.
С педагогической точки зрения для учителя важно, что в процессе реализации рассмотренного сценария ученик самостоятельно обнаруживает закономерность, самостоятельно даёт или пытается дать её словесное выражение. В результате теорема становится результатом личной деятельности, а не внешним фактом, пусть и пришедшим из авторитетного источника.
|
|
|
С математической точки зрения важно, что в процессе реализации сценария становится ясен метод доказательства, причём его суть легко поддаётся словесному выражению – метод подобия. Интересно, что после реализации сценария педагог приобретает большую свободу действий. Можно построить аналитическое рассуждение, приведшее к рис. 17 и, как следствие, к найденному доказательству. Можно использовать метод подобия другим способом, проведя через вершину треугольника прямую, параллельную одной из его сторон. Можно рассмотреть совсем другое доказательство, основанное на теореме Фалеса, или третье доказательство, основанное на методе площадей. Все это методико-математическое богатство описано в книге [44, разд. 1].
С методологической точки зрения важна последовательность действий: качественное наблюдение и простой вычислительный эксперимент, приводящий к гипотезе; тонкий вычислительный эксперимент, «опровергающий» гипотезу; снятие противоречия с помощью дедуктивного доказательства. Заметим, что для человека, научное мировоззрение которого находится в процессе формирования, ситуация является достаточно сложной. Действительно, когда 13- или 14-летний ребёнок смотрит на каплю воды невооружённым глазом, то она кажется ему блестящей, чистой и прозрачной. Когда же он рассматривает её в микроскоп, то видит в ней песчинку, соринку и инфузорию-туфельку. Таким образом, грубый инструмент (глаз) и тонкий инструмент (микроскоп) дают разные ответы на вопрос о структуре капли воды.
Сравнение эксперимента с каплей и эксперимента с биссектрисой выявляет одно из различий между физическим и математическим экспериментом. Во-первых, долго или коротко, но выясняется, что при изучении капли истину показывает более точный инструмент, а при изучении биссектрисы – более грубый. Во-вторых, и это главное, при изучении капли «противоречие в показаниях инструментов» разрешается с помощью дальнейших экспериментов, а при изучении биссектрисы экспериментальное разрешение противоречия невозможно, так что приходится прибегать к дедуктивным рассуждениям. Мы ещё не раз будем встречаться с таким обстоятельством.
Повторный эксперимент, или
Дата добавления: 2019-09-13; просмотров: 851; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!