Роль эксперимента в обнаружении теорем-критериев, или
Признак параллельности прямых
Хорошо известно, что теоремы-критерии играют в математике особую роль, поскольку позволяют сравнительно легко установить наличие или отсутствие интересующего нас свойства математического объекта. Пусть, например, нам нужно установить делимость на 3 некоего 20-значного числа. Из-за большой величины это число невозможно даже набрать на обычном инженерном калькуляторе, однако его делимость на 3 легко устанавливается с помощью критерия делимости: число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3.
Очевидно, что изучению теорем-критериев следует уделять повышенное внимание. Это относится, в частности, к этапу обнаружения теоремы. В этой связи рассмотрим одну задачу о параллельных прямых, которая предлагается учащимся до того, как изучен признак параллельности.
Задача. На чертеже, выполненном учителем в среде GeoGebra, нарисованы две пары прямых: пунктирные прямые 
и 
и обычные прямые 
и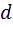 
(рис. 21). Внешне все выглядит так, как будто прямые попарно параллельны: 
и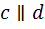 
. Известно, однако, что на самом деле одна и только одна параллельность имеет место. Проведя дополнительные построения и измерения, выясните, которая пара состоит из параллельных прямых. При этом запрещается следующее: открывать панель объектов, вводить на полотно GeoGebra оси координат и сетку, увеличивать точность округления, выходить за пределы экрана.
|
|
|
Рис. 21. Где параллельность?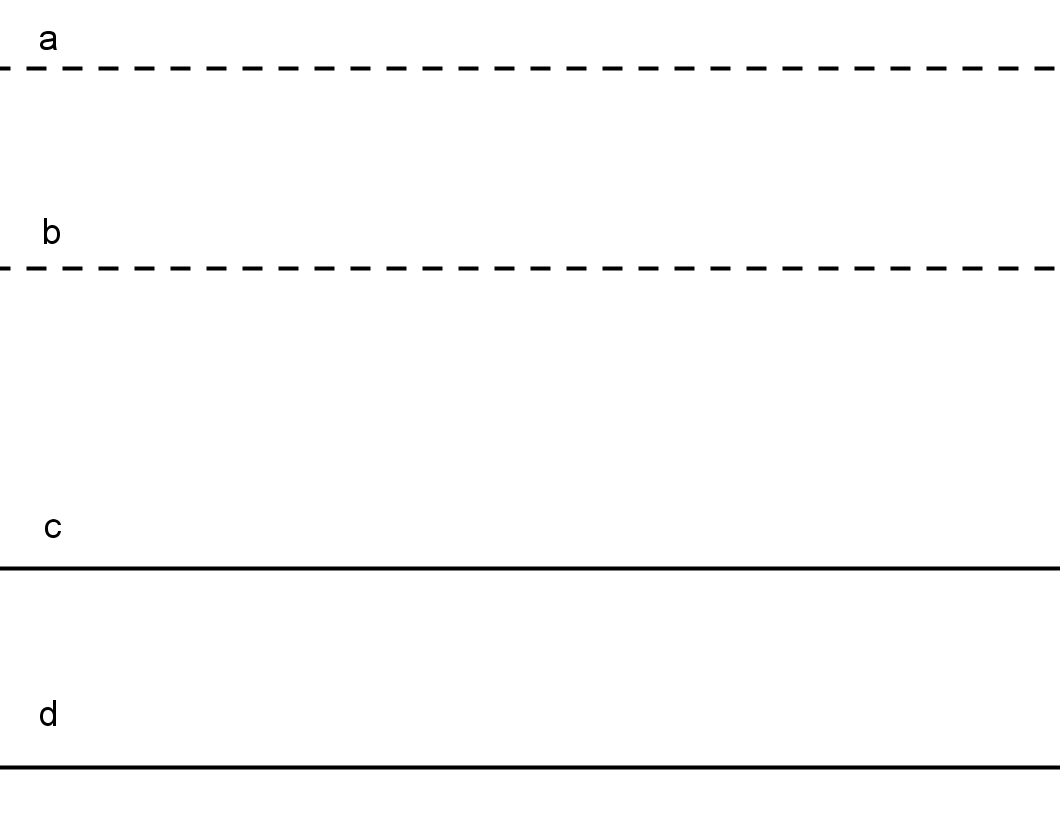 
Обсуждение задачи начнём с замечания о том, что запреты достаточно точно воспроизводят обстановку измерений на местности. Действительно, на местности нет ни осей, ни сетки, ни координат точек, ни уравнений прямых. Точность измерения приборов является фиксированной. Как правило, крайне трудно выйти за пределы изучаемого участка земли, а выйти за него на большое расстояние и продолжить измерения просто невозможно. В этих условиях попытаемся воспользоваться нашими знаниями о параллельных прямых, пока крайне скудными.
Первый эксперимент и первая неудача. На момент получения задачи школьникам известно, что две прямые, перпендикулярные третьей, не пересекаются [1, c. 23]. Этот факт подсказывает нам следующие действия: 1) выбрать на прямой какую-либо точку; 2) опустить перпендикуляр на прямую ; 3) измерить углы между построенным отрезком и каждой из прямых и ; 4) проделать те же самые действия 1–3 применительно к прямым и 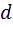; 5) дать геометрическое истолкование полученным результатам.
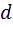Вот здесь школьника подстерегает неудача. Дело в том, что все четыре измеренных угла оказываются прямыми. Получается, что прямые и перпендикулярны первому из построенных отрезков, то есть параллельны между собой, а прямые и перпендикулярны второму из построенных отрезков, то есть тоже параллельны между собой. Между тем, по условию задачи имеет место только одна параллельность.
|
|
|
Второй эксперимент и вновь неудача. На момент получения задачи школьники обладают только теми теоретическими знаниями о параллельных, которые использовались (неудачно!) в первом эксперименте. Придётся действовать в соответствии со здравым смыслом.
Рассмотрим две заведомо не параллельные прямые и две точки на одной из них. Если из этих точек опустить перпендикуляры на другую прямую, то они должны быть разной длины. При этом разница между их длинами должна быть тем больше, чем дальше друг от друга отстоят исходные точки. Это рассуждение подсказывает следующие действия: 1) выбрать на прямой две точк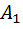и, 
и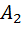 
, первую возле левого края экрана, а вторую возле правого; 2) из выбранных точек опустить перпендикуляры 
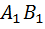и 
на прямую (здесь 
3) измерить их длины; 4) проделать те же самые действия 1–3 применительно к прямым и 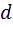; 5) дать геометрическое истолкование полученным результатам.
Здесь школьников вновь подстерегает неудача, поскольку длины построенных отрезков оказываются равным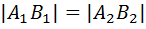и: 
и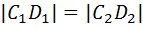 
. Как бы ни трактовать равенство длин, мы придем к противоречию. Действительно, если мы предположим, что из равенства 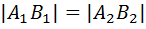вытекает параллельность , то придется считать, что из равенства 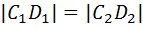вытекает параллельность 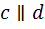, а наличие двух параллельностей противоречит условию задачи. Если же мы предположим, что из равенства 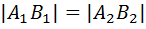вытекает «непрараллельность» 
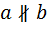, то придется считать, что из равенства 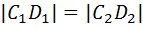также вытекает «непараллельность» 
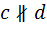. Отсутствие хотя бы одной параллельности также противоречит условию задачи.
|
|
|
Итак, две неудачи подряд говорят о том, что перед очередным экспериментом необходимо провести хороший теоретический анализ.
Элементы теоретического анализа. Обратим внимание на то, что при проведении первого эксперимента участвующие в нем линии играли различные роли: прямые и были объектами изучения, а отрезок, соединяющий две точки на них, выступал в качестве инструмента изучения. При этом мы анализировали взаимное расположение (вновь основной вопрос!) прямых и отрезка, то есть объекта и инструмента.
В связи с этим поставим простой для учителя (но не для школьников!) вопрос: как ввести числовую характеристику взаимного расположения двух прямых? Очевидно, что такой характеристикой является величина угла, точнее говоря, величина одного из четырёх углов, образующихся при пересечении двух прямых.
|
|
|
Пересечём изучаемые прямые и третьей прямой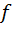 
и попытаемся сравнить взаимные расположения двух пар объектов: прямых и 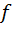, с одной стороны, и прямых и 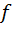, с другой стороны. Очевидно, что изучаемые прямые расположены по отношению ко вспомогательной прямой 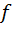либо одинаково, либо по-разному. В первом случае должны быть равны между собой те два угла, которые характеризуют взаимное расположение каждой из изучаемых прямых и вспомогательной прямой. Во втором случае эти углы должны быть различными. Проще говоря, нужно сравнить угол между прямыми и 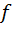и угол между прямыми и .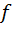
Для единообразного способа сравнения углов примем следующее соглашение: будем рассматривать углы, лежащие одновременно по разные стороны от прямой 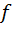и между прямыми и (накрест лежащие) [1, c. 53].
Теперь мы можем приступить к третьему эксперименту.
Третий эксперимент и гипотеза. Выберем по точке на прямых и , соединим их отрезком и измерим накрест лежащие углы. Проделаем те же самые построения для другой пары прямых: выберем по точке на прямых и 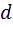, соединим их отрезком и измерим накрест лежащие углы.
Удивительно, но результаты измерений будут сильно отличаться друг от друга! Для прямых и накрест лежащие углы окажутся равными. Они будут оставаться равными при любых перемещениях выбранных точек. Во втором случае все будет иначе. Действительно, для одних отрезков накрест лежащие углы окажутся равными, однако найдутся такие отрезки, для которых накрест лежащие углы будут отличаться друг от друга. На рис. 22 отмечено равенство накрест лежащих углов для прямых и и отличие некоторых накрест лежащих углов для прямых и .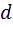
Любой эксперимент делается для того, чтобы его результаты получили некое содержательное истолкование. В нашем случае такое истолкование может иметь вид Гипотезы: прямые и одинаково расположены относительно любого пересекающего их отрезка, поэтому они параллельны; прямые и 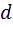имеют разное расположение относительно пересекающих их отрезков, поэтому они не параллельны.
Разумеется, наша гипотеза не является точным решением задачи, хотя и выглядит весьма правдоподобной. Для этого нужно сформулировать и доказать критерий параллельности прямых.
Рис. 22. Пунктирные прямые параллельны?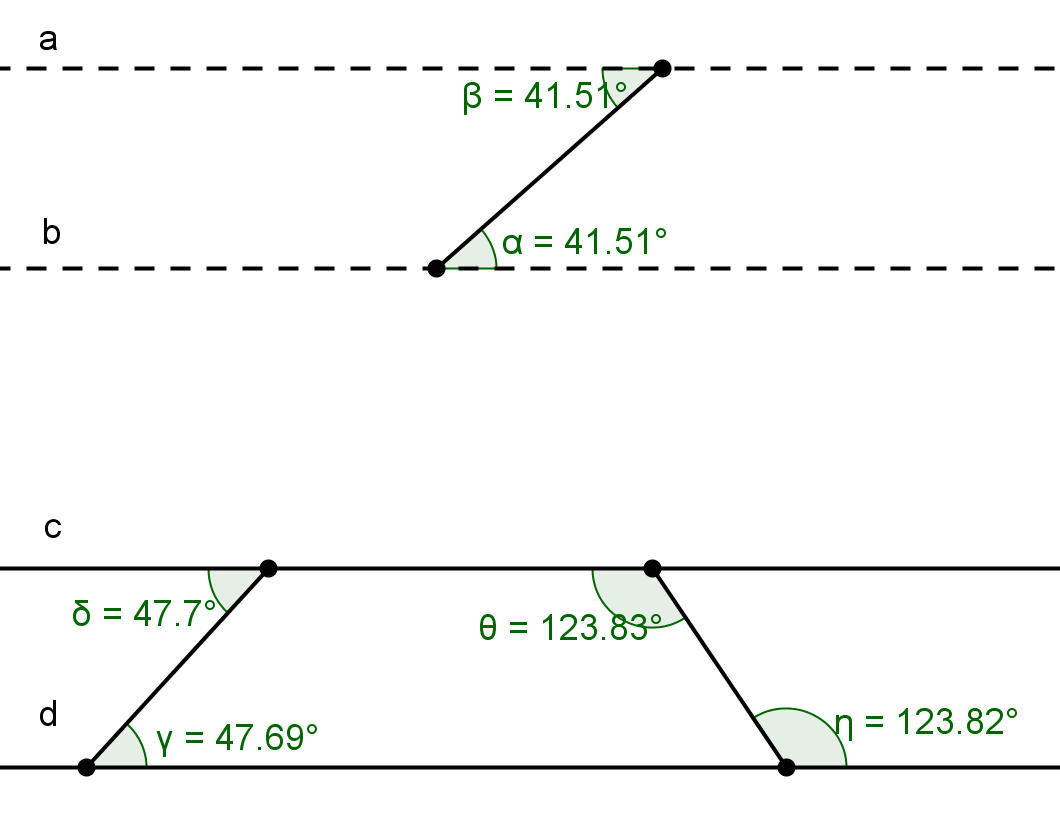 
Впрочем, теперь школьники-экспериментаторы находятся «в одном шаге» от формулировки теоремы, а доказательство может быть выполнено стандартным способом [1, c. 53–54].
В заключение раздела раскроем «тайну» построения прямых на рис. 21 и 22. Она заключена в следующей таблице.
| Обозначения | Координаты | Расположение прямой |
| 
| Горизонтальная прямая. |
| 
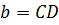
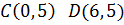
| Горизонтальная прямая. |
| 
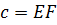
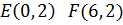
| Горизонтальная прямая. |
| 
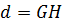
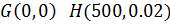
| Наклонная прямая,
угловой коэффициент  .
|
Очевидно, что горизонтальные прямые и параллельны, а горизонтальная прямая не параллельна наклонной прямой 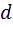. Интересно, что инструменты Перпендикуляр и Расстояние оказываются недостаточно чуткими для того, чтобы обнаружить слабый наклон прямой 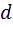, а инструмент Угол обнаруживает «какой-то непорядок», который служит косвенным свидетельством непараллельности прямых.
О продуктивных сценариях и
Математических экспериментах
Итак, мы рассмотрели продуктивные сценарии изучения четырёх важных теорем школьного курса математики. Сценарии характерны тем, что в процессе их реализации школьники имеют возможность повторного изобретения изучаемых теорем, причём практически самостоятельно или с минимальной помощью учителя. В связи с этим несколько обстоятельств заслуживают отдельного анализа.
Прежде всего, очевидно, что переработка обычного, рутинного изучения теорем по школьному учебнику в продуктивный сценарий не столь уж трудна и не требует какого бы то ни было изменения школьной программы. Просто нужно уделять внимание деталям процесса изобретения теорем и не «спрямлять» этот процесс, пропуская его этапы.
Кроме того, очевидно, что реализация продуктивных сценариев требует несколько большего времени, чем тратится обычно при буквальном следовании школьному учебнику. С одной стороны, противоречие между необходимым временем и временем, имеющимся в наличии, носит объективный характер и должно учитываться в той или иной форме. С другой стороны, автор убеждён, что выявленное противоречие не столь уж велико и может быть преодолено за счёт мастерства учителя. Во всяком случае, следует приложить усилия для его преодоления, поскольку потенциальный выигрыш от реализации продуктивных сценариев весьма велик.
Наконец, обращает на себя внимание тот факт, что во всех четырёх сценариях мы использовали математический эксперимент. Парадоксально, но в рамках данной книги использование эксперимента является обстоятельством предопределённым и случайным одновременно. С одной стороны, естественно предположить, что рассмотренные теоремы были изобретены (или открыты) именно в процессе экспериментальной деятельности математиков древности, так что повторное изобретение теорем школьниками является своего рода исторической реконструкцией. В этом смысле использование эксперимента является предопределённым. С другой стороны, вполне возможно, что для других теорем школьного курса предпочтительными окажутся продуктивные сценарии чисто теоретической природы. В этом смысле обсуждение эксперимента в рамках данной книги является случайным.
Интересно, что рассмотренные сценарии обладают неким, если так можно выразиться, «стилистическим единством». Действительно, теоретические рассуждения и эксперимент оказываются неотделимыми друг от друга; эксперимент естественным образом порождает правдоподобную гипотезу, а более точный эксперимент уменьшает её правдоподобие; единственным «арбитром» в «конфликте» двух экспериментов оказывается дедуктивное рассуждение… Мы обсудим взаимодействие теоретического и экспериментального начал математики в разделе «Приложение».
Дата добавления: 2019-09-13; просмотров: 182; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!