О повторном изобретении определений школьниками

⇐ ПредыдущаяСтр 13 из 24Следующая ⇒

Как уже говорилось, математикам приходится изобретать новые определения для обозначения и формализации тех явлений, с которыми им приходится сталкиваться. Если мы хотим приобщить наших учеников к процессу изобретения определений, нам придётся создать для этого специальные сценарии, в процессе реализации которых школьники будут совершать некоторые умственные действия, проделанные ранее математиками-первооткрывателями. Другими словами, нам придётся придерживаться линии поведения, которую ранее мы назвали «Инструментальной мастерской»:

· создать продуктивные сценарии изучения всех определений школьного курса математики;

· решать в экспериментальном порядке и с учётом конкретных педагогических условий все вопросы, связанные с использованием продуктивных сценариев: использовать ли их вообще, использовать систематически или эпизодически, какова должна быть частота их систематического использования, каковы те конкретные определения, изучение которых даёт наибольший развивающий эффект, и т.д.

Если определённая часть педагогического сообщества будет придерживаться описанной линии поведения, то естественно предположить, что с течением времени конкретные сценарии будут совершенствоваться, библиотека сценариев будет пополняться, а опыт использования продуктивных сценариев будут накапливаться. В результате возникнет по-настоящему эффективная коллекция педагогических инструментов, которая позволит реализовать исследовательски ориентированное обучение математике в школе.

Возможно, читатель заметил следующее: по поводу изучения определений автор высказывает то же самое суждение, которое было высказано ранее по поводу изучения теорем. Сделано это сознательно, причём почти в тех же словах, потому что автор убеждён в его справедливости. В то же время, изобретение теорем и изобретение определений – это два разных процесса, и автор совершенно по-разному оценивает роли школьников, участвующих в них.

С одной стороны, автор высоко оценивает способность школьников повторно изобретать математические теоремы. В этом его убеждает личный опыт математической деятельности в студенческие, аспирантские и последующие годы, относительная простота конструирования продуктивных сценариев, а также, и это главное, многочисленные примеры «переоткрытий» теорем школьниками, которые автор наблюдал в своей педагогической практике. С другой стороны, автор достаточно низко оценивает способность школьников повторно изобретать математические определения. Такой пессимизм (не побоимся этого слова) основан как на объективной стороне дела, так и на его субъективном восприятии. Действительно, изобретение определений, равно как и изобретение теорем, является неформализуемым, внелогическим процессом. Однако для изобретателя теорем существует «помощь» в виде разнообразных эвристик, экспериментов, правдоподобных рассуждений в смысле Д. Пойа [23], а для изобретателя определений такой «помощи» не существует. К тому же не следует забывать, что речь идёт о детях, совсем не имеющих опыта выявления сущности математических объектов и выражения этой сущности в виде текстов. Будучи математиком, автор отчётливо помнит, какого напряжения требовало от него конструирование новых определений, и понимает, что было бы нереалистичным рассчитывать на такие же усилия со стороны школьников. Впрочем, не все так безнадёжно. Как бы ни относиться к оптимизму-пессимизму того, другого или третьего автора, следует делать то, что возможно. Сосредоточимся на позитивном.

По-видимому, человеческий мозг имеет эволюционно сложившееся, «синергетическое» свойство организовывать поступающую информацию в такие группы, которые удобны для запоминания. На бытовом уровне это проявляется, например, в структуре телефонных номеров. Так, никто не запоминает телефон в виде 731986 (семьсот тридцать одна тысяча девятьсот восемьдесят шесть), а представляет его в виде 73-19-86. Причина в том, что в первом случае придётся запомнить шесть единиц информации, а во втором случае – только три. При этом телефон 45-84-58 скорее всего запомнится в виде 458-458 (две единицы информации).

Нечто подобное происходит с математикой на школьном уровне. Когда-то математиками древности было замечено, что середина отрезка играет особую роль, поскольку участвует во многих теоремах, в частности, в теоремах о треугольниках. Очевидно, что было бы неудобно в разных ситуациях и по много раз повторять весьма длинное словосочетание «отрезок, соединяющий вершину треугольника с серединой противоположной стороны». Вместо него когда-то был введён краткий и выразительный термин «медиана». Вместо длинного словосочетания «самая длинная сторона прямоугольного треугольника» был введён термин «гипотенуза». Таких примеров много.

Происхождение некоторых терминов-сокращений существенно сложнее и не сводится к простому наблюдению и желанию сделать математическую речь краткой и выразительной. Дело в том, что они могут быть введены только после доказательства той или иной теоремы. Таков, например, термин «центроид» приобретает смысл только после того, как доказана теорема о том, что все медианы треугольника пересекаются в одной точке. Таков же термин «ортоцентр» – точка пересечения высот треугольника, а также нечасто употребляющийся термин «инцентр» – точка пересечения биссектрис треугольника.

Впрочем, усвоение терминов вышеописанных типов не является слишком трудным для школьников. Настоящую трудность представляют собой такие понятия, которые затрагивают сущность изучаемых явлений. Руководствуясь своими личными взглядами, приведём список таких понятий в виде таблицы. Читатель легко может составить

Раздел	Понятие
Геометрия	Расстояние от точки до геометрической фигуры Длина, площадь, объем
Алгебра	Простое число Иррациональное число Предел последовательности
Стохастика	Вероятность события
Анализ	Функция Предел функции Непрерывность функции Производная функции

свой собственный список объективно сложных и трудных для школьника понятий. При этом он может использовать неплохой теоретико-прагматический критерий трудности конкретного понятия: если удаётся сконструировать или найти в литературе продуктивный сценарий изучения понятия, значит, трудность его усвоения не слишком велика.

Поясним один неочевидный элемент содержания таблицы: понятие предела последовательности помещено в раздел алгебры. Дело в том, что без понятия (или предпонятия) предела последовательности крайне трудно или невозможно понять, что такое сумма (произведение) иррациональных чисел. Следовательно, останется по существу не понятым понятие площади прямоугольника с иррациональными сторонами.

Повторимся: автор не возьмёт на себя смелость утверждать, что он может составить продуктивные сценарии изучения всех понятий, приведённых в таблице. Тем не менее, некоторые шаги в этом направлении удаётся сделать. Так, в книге [40, разд. 6.2] описан натурный эксперимент, который подводит школьников к самостоятельному усвоению понятия «вероятность события». В разделе 3.2 настоящей книги приведён продуктивный сценарий изучения понятия «расстояние от точки до геометрической фигуры», а также вытекающая из процесса изучения исследовательская программа для школьников. В разделе 3.3 приведён компьютерный эксперимент, который позволяет естественным образом ввести понятие «числовая мера разносторонности треугольника». Наконец, в данном разделе мы приведём продуктивный сценарий изучения понятия простого числа.

Примем следующее соглашение: каждый педагогический сценарий предлагается учащимся в тот момент, когда они ничего не знают о предмете изучения.

ПРОСТОЕ ЧИСЛО

Наш сценарий основан на решении двух задач и анализе этих решений.

Задача 1. Для каждого из чисел 1, 2, …, 12 выпишите все натуральные делители. Разбейте множество на несколько групп в соответствии с количеством делителей. Целесообразно ли применять этот способ разбиения ко всему множеству натуральных чисел?

Обсуждение. Первые две части задачи являются простыми и даже примитивными, поскольку требование разбить какое-либо множество на группы встречается детям уже в первом классе, основание для разбиения указано явно, а делители находятся просто, о чем свидетельствует следующая таблица. Теперь множество 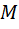разбивается на пять групп. В первую группу входит одно число 1, имеющее точно один делитель; во вторую группу входит пять чисел, имеющих по два делителя каждое; в

Число	1	2	3	4	5	6	7	8	9	10	11	12
Делит.	1	1, 2	1, 3	1, 4, 2	1, 5	1, 6, 2,3	1, 7	1, 8, 2, 4	1, 9, 3	1, 10, 2, 5	1, 11	1, 12, 2, 3, 4, 6
Кол-во делит.	1	2	2	3	2	4	2	4	3	4	2	6

третью группу 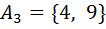входит два числа, имеющих по три делителя каждое; в четвертую группу 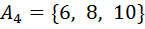входит три числа, имеющих по 4 делителя каждое; наконец, в последнюю группу 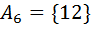входит единственное число из множества 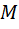, имеющее шесть делителей.

Третья часть задачи существенно сложнее для школьников, чем первые две части, поскольку она непривычна и носит теоретический или даже методологический характер. Тем не менее, попытаемся извлечь общее суждение из некоторых конкретных вычислений.

Попытаемся, например, найти какие-нибудь делители 18-значного числа 235764911583123343. Прежде всего, последняя цифра числа показывает, что оно не делится на 2 и, следовательно, ни на одно чётное число. Кроме того, оно не делится на 5 и, следовательно, ни на одно число, кратное пяти. Сумма цифр этого числа равна 70, следовательно, оно не делится на 3 и ни на одно число, кратное трём. Проверим, является ли число 7 делителем изучаемого числа. Даже эта, казалось бы, простая проверка оказывается трудоёмкой. Действительно, изучаемое число не может быть набрано на обычном инженерном калькуляторе, поскольку количество цифр в нем слишком велико. Школьнику остаётся выполнить деление в столбик, которое, и автор проверил это, заканчивается неудачей. И что же делать дальше?

Конечно, можно проявить упорство (а в данном случае упрямство) и попытаться искать другие делители, однако уже на данном этапе размышлений видно, что способ, вполне хороший для разбиения на группы первых 12-ти чисел натурального ряда, совсем не годится для больших чисел и должен быть отвергнут. Итак, нецелесообразно применять описанный способ разбиения на группы к натуральному ряду в целом.

Формально задача 1 решена, однако результат порождает некую неудовлетворённость. Действительно, интуитивно ясно, что количество делителей является некоторой существенной характеристикой числа, подобно тому, как существенными характеристиками являются количество его разрядов, его чётность или нечётность и т.п. Так возникает новая задача, которая имеет почти гуманитарный характер.

Задача 2. Придумайте метод разбиения натурального ряда на группы чисел, связанный с количеством его делителей. Дайте имена выявленным группам.

Обсуждение. Вычисления, проделанные при составлении таблицы, дают определённую информацию для решения задачи.

Во-первых, очевидно, что число 1 уникально в том смысле, что не существует другого натурального числа, которое имело бы точно один делитель. Следовательно, целесообразно исключить число 1 из списка натуральных чисел и делить на группы только оставшееся множество .

Во-вторых, очевидно, что каждое число 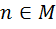имеет в качестве делителей числа 1 и 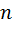, то есть имеет не менее двух делителей.

В-третьих, как видно из примеров, встречаются числа, имеющие точно два делителя, и числа, имеющие более двух делителей.

Так выявляются два типа чисел из множества 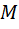: числа, имеющие точно два делителя, и числа, имеющие более двух делителей. Конечно, такая классификация чисел «грубее» той, что была получена при решении задачи 1, зато она снимает проблему нахождения делителей больших чисел. Действительно, любое число имеет либо точно два делителя, либо более двух, и третьего не дано, и при этом совершенно неважно, известен ли нам список этих делителей.

Осталось дать имена найденным типам чисел. Для этого проделаем простой эксперимент из области, граничащей с арифметикой и литературой одновременно: запишем числа из выявленных классов в виде произведений, располагая множители в порядке их неубывания. Вот тут и выявляется существенная разница между числами из наших групп. Числа из первой группы могут быть записаны в виде произведения единственным образом. Так, 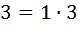, 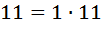и т.п. Числа из второй группы могут быть записаны в виде произведения несколькими способами. Так, , 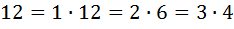и т.п. Очевидно, что единственность разложения на множители говорит об относительной простоте числа, а наличие нескольких разложений – о его относительной сложности.

Так возникает традиционное определение: натуральное число 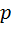, большее 1, называется простым, если оно имеет только два натуральных делителя, 1 и 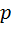; в противном случае оно называется составным.

Итак, задача 2 решена. Как обычно, решённая задача порождает разнообразные вопросы. Остановимся на двух из них, математическом и педагогическом.

Когда перед математиком (в частности, школьником) возникает новое определение, поначалу всегда стоит вопрос о том, насколько оно полезно или бесполезно. Ответ прост: чем больше содержательных теорем удаётся доказать на основе нового определения, тем более оно полезно, тем более существенны свойства математического объекта, описанные определением. Специфика арифметики состоит в том, что глубокие теоремы о простых числах могут быть доказаны непосредственно после их определения. Таковы теоремы о бесконечности множества простых чисел и о разложении натурального числа на простые множители. При доказательстве используются классические методы дедуктивных рассуждений – метод от противного и метод математической индукции соответственно.

Педагогический вопрос состоит в том, насколько полезен или бесполезен описанный выше сценарий введения понятия простого числа. По-видимому, ответ на этот вопрос заключён в сущности сценария: учитель конструирует определение вместе со школьниками. Прежде всего, мы видим три субъекта деятельности: учителя, отдельного ученика и класс как единое целое [45]. Кроме того, мы говорим о совместной деятельности этих субъектов. Наконец, и это главное, определение именно сконструировано, а не предъявлено и предложено для запоминания. Благодаря такому сценарию происходит знакомство школьника с элементами работы математиков-исследователей. Благодаря такому сценарию математик становится педагогом, а педагог – математиком.

Дата добавления: 2019-09-13; просмотров: 182; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 8 9 10 11 121314 15 16 17 Следующая ⇒

Мы поможем в написании ваших работ!