Напряжения на наклонных площадках

⇐ ПредыдущаяСтр 2 из 2

Рассмотрим, как будут изменяться напряжения на гранях малого элемента (рис. 4.3, а) при его повороте на угол a (рис. 4.3, б). Учитывая бесконечно малые размеры элемента, можно считать, что напряжения, например, на грани ВС (рис. 4.3, б) будут такими же, как и на наклонной (под углом a) площадке В₁С₁ (рис. 4.3, а).

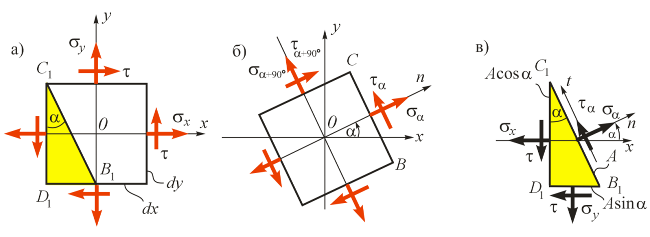
Рис. 4.3. Напряжения на наклонных площадках при двухосном напряженном состоянии

Площадь наклонной грани треугольного элемента обозначим A, тогда площади нижней и левой граней будут равны A·sin a и A·cos a, соответственно. Составим уравнения равновесия Sn = 0 и St = 0 для треугольного элемента B₁C₁D₁ (рис. 4.3, в).

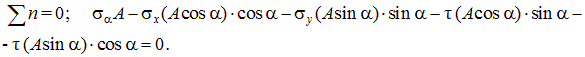
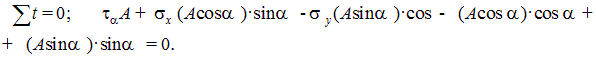
Из этих равенств находим:

;

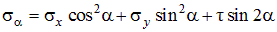(4.2)

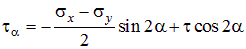(4.3)

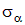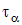Полученные соотношения свидетельствуют, что и являются периодическими функциями от α с периодом π. Следовательно, каждая из этих функций в указанном периоде достигает максимальных и минимальных значений.

Найдем нормальные и касательные напряжения на площадке, повернутой на угол a + 90^о (рис. 4.3, б):

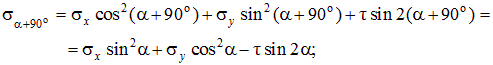
(4.4)

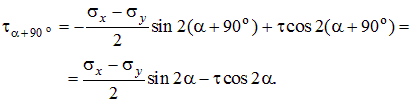
(4.5)

Складывая нормальные напряжения s_a и s_a₊₉₀, получим

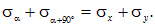
(4.6)

Формула (4.6) выражает свойство инвариантности нормальных напряжений, которое формулируется следующим образом: сумма нормальных напряжений в точке по двум взаимно перпендикулярным направлениям есть величина постоянная.

Исследуя выражения для t_a и t_a₊₉₀^о, можно заметить, что касательные напряжения, действующие на смежных взаимно перпендикулярных площадках, равны, но имеют разные знаки, что, казалось бы, противоречит принятому ранее правилу знаков для касательных напряжений и закону их парности. Однако, такой результат подтверждает приведенные ранее определения. В принятой при рассмотрении равновесия малого элемента локальной системе координат положительный знак определяется совпадением его направления с локальной осью t. При этом, положительное напряжение t_a стремится повернуть малый элемент против часовой стрелки и направлено к общему ребру. Отрицательное значение напряжения t_a₊₉₀^о лишь подтверждает закон парности касательных напряжений, так как оно в этом случае также направлено к общему ребру (стремясь повернуть малый элемент по часовой стрелке) и равно t_a по абсолютной величине.

Главные напряжения. Дифференцируя равенство (4.2) и приравнивая производную функции s_a (a) нулю, получим

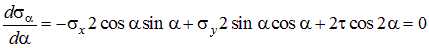(4.7)

Из (4.7) следует

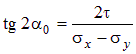(4.8)

где 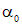– значение угла 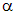, при котором 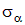имеет экстремум. Полученное уравнение имеет два решения 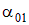и 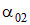, отличающихся на π/2:

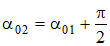
(4.9)

Направления, определяемые углам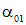и и 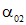, называются главными направлениями, а площадки, перпендикулярные этим направлениям, называются главными площадками. На этих площадках действуют максимальное s₁ = s_max и минимальное s₂ = s_min нормальные напряжения, которые называются главными напряжениями. При этом s₁ больше s₂ в алгебраическом смысле (например, s₁= +20 МПа, а s₂= – 100 МПа)._.

Выражение (4.8) не позволяет однозначно ответить на вопрос, какой из двух углов 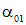или 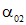указывает именно первое (или второе) главное направление. Поэтому более удобно пользоваться формулами (даются без вывода):

;

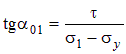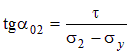(4.10)

Нетрудно заметить, что если t_a из (4.3) приравнять нулю, то также получим равенство (4.8). Отсюда следует, что на главных площадках касательные напряжения равны нулю. Таким образом, полное определение главных площадок формулируется следующим образом.

Главными площадками называются такие площадки, на которых нормальные напряжения экстремальны, а касательные напряжения равны нулю.

Чтобы получить формулы для главных напряжений, преобразуем выражения (4.2) и (4.4), с использованием известных тригонометрических соотношений cos²a = (1+cos 2a)/2 и sin²a = (1– cos 2a)/2 и запишем их вместе, причем верхние знаки соответствуют напряжению s_a = s₁ = s_max, а нижние – s_a₊₉₀о = s₂ = s_{min .}

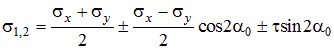(4.11)

Представив выражение (4.8) в виде

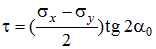и подставляя его в (4.11), после несложных преобразований с использованием формул тригонометрии, получим

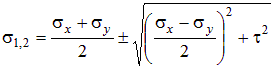(4.12)

В этой формуле записаны сразу два выражения, одно – для определения s₁ =s_max (используется знак «+» перед квадратным корнем), а второе – для определения s₂=s_min (используется знак «–»).

Если сложить s₁и s₂, получим

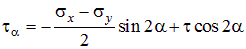
(4.13)

что подтверждает свойство инвариантности суммы нормальных напряжений, т.е. то, что сумма нормальных напряжений по двум взаимно перпендикулярным направлениям не зависит от угла.

На рис. 4.4, а показан исходный элемент, вырезанный вблизи некоторой точки тела, а на рис. 4.4, б – элемент, грани которого совпадают с главными площадками (направления главных осей 1 и 2 выбраны произвольно).

То, что экстремальные нормальные напряжения названы главными, не случайно. Именно по значениям этих напряжений можно провести оценку прочности материала.

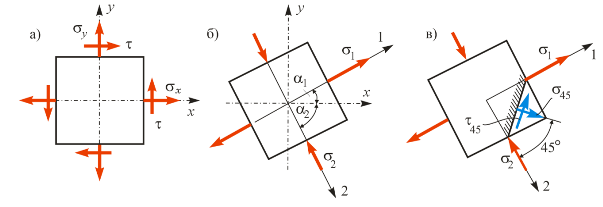
Рис. 4.4. К определению главных и максимальных касательных напряжений

Экстремальные касательные напряжения. Для некоторых материалов причиной разрушения или потери эксплуатационных свойств могут являться не нормальные, а касательные напряжения. Может возникнуть такое напряженное состояние в точке, когда нормальные напряжения еще не превышают своих опасных значений (s_max < s_o), но касательные напряжения уже будут больше их опасных значений (t_max > t_o). Поэтому необходимо знать величины экстремальных касательных напряжений и углы наклона площадок, на которых они действуют.

Углы наклона площадок с экстремальными значениями касательных напряжений можно найти, вычисляя производную функции t_a (4.3) по a и приравнивая ее нулю:

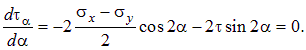
(4.14)

Обозначая через b₀ угол наклона нормали к площадке с экстремальными касательными напряжениями, из (4.14) получим формулу для определения этого угла:

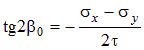
(4.15)

Сравнивая (4.8) с (4.15), можно записать следующее равенство

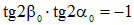
(4.16)

откуда следует, что b₀ = a₀ + 45°, т.е. нормаль к площадке с экстремальными касательными напряжениями составляет угол 45° с нормалью к площадке, на которой действуют главные напряжения (рис. 4.4,в).

Найдем значения экстремальных касательных напряжений. Для этого запишем в одном выражении (как это было сделано раньше для нормальных напряжений) для t_max,min формулы (4.3) и (4.5) относительно главных направлений, подставляя угол a = 45° и учитывая равенство нулю касательных напряжений t на главных площадках:

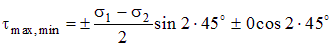(4.17)

Окончательно получаем формулу для определения экстремальных касательных напряжений:

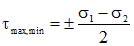(4.18)

Используя формулы (4.8) и (4.10) для нормальных напряжений, подставляя угол a = 45^°, получим выражение для нормальных напряжений, действующих на площадке с экстремальными касательными напряжениями:

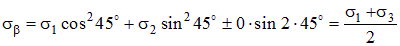(4.19)

Можно показать, что на всех площадках с экстремальными касательными напряжениями будут действовать одинаковые по величине нормальные напряжения s_b:

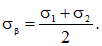
(4.20)

Знак «+» в (4.18) относится к максимальным касательным напряжениям, а «–» к минимальным касательным напряжениям. Однако следует отметить, что знак касательного напряжения не имеет особого значения и физического смысла; он определяет только его направление в отличие от знака нормального напряжения, соответствующего сжатию («–») или растяжению («+»), что совсем не безразлично, так как хрупкие материалы значительно хуже работают на растяжение, чем на сжатие. Поэтому в дальнейшем нас будет интересовать величина экстремального касательного напряжения, взятая по модулю.

На рис. 4.4, в показана площадка (заштрихована), на которой действуют t₄₅ = t_min = – (s₁ – s₂)/2 и s₄₅ = s_b = (s₁ + s₂)/2 .

Закон Гука при двухосном напряженном состоянии. Рассмотрим деформированное состояние элемента, на гранях которого действуют два нормальных напряжения s_x и s_y (рис. 4.5,а). Вычислим деформацию 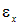, используя принцип независимости действия сил, в соответствии с которым

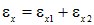(4.21)

где 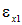– деформация, обусловленная действием напряжений 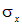(рис. 4.5, б), а 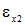– действием напряжений 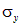(рис. 4.5,в).

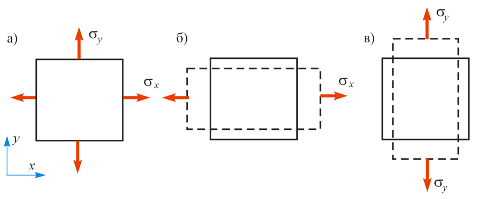
Рис. 4.5. К выводу закона Гука при двухосном напряженном состоянии

Согласно закону Гука для одноосного напряженного состояния 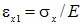. Деформации 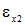по отношению к направлению действия напряжений 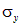являются поперечными деформациями и могут быть выражены при помощи коэффициента Пуассона: 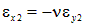. В свою очередь, 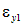также вычисляется из закона Гука: 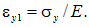В свою очередь .

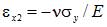Складываем 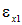и 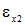, а затем 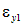и :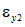

;

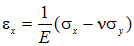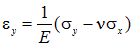(4.22)

Соотношения (4.22) называются законом Гука для линейных деформаций при двухосном напряженном состоянии. Исследования показывают, что касательные напряжения не оказывают влияния на линейные деформации. Связь между касательными напряжениями и угловыми деформациями будет рассмотрена в последующих главах при изучении кручения.

Обобщенный закон Гука. По аналогии с формулами (4.22), связывающими линейные деформации с нормальными напряжениями, можно написать соотношения для трехосного напряженного состояния, показанного на рис. 4.1:


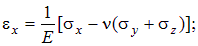
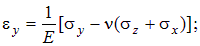
		(4.23)
	.

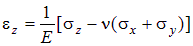Равенства (4.23) называются обобщенным законом Гука для линейных деформаций. Если перейти к главным напряжениям, то в (4.23) следует заменить индексы x, y, z на 1, 2, 3.


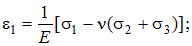
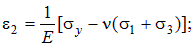
		(4.24)
	.

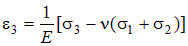Понятие о теориях прочности

Рассмотренный метод расчета на прочность при одноосном нагружении, то есть, при растяжении (сжатии) стержней и основная расчетная формула основаны на предположении, что причиной разрушения или необратимых пластических деформаций являются максимальные нормальные напряжения .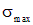

Однако, для некоторых хрупких материалов их разрушение может произойти из-за касательных напряжений. Приведенный ранее пример разрушения чугунного образца под углом в 45^о указывает на то, что в этом случае причиной разрушения являются максимальные касательные напряжения 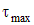. Ранее было показано, что при одноосном напряженном состоянии .

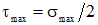Условия прочности для одноосного напряженного состояния можно записать следующим образом

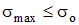	,	(4.25,а)
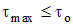	,	(4.25,б)

где 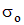и 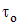– опасные нормальное и касательное напряжения, полученные из испытаний образцов при растяжении и сжатии (одноосное нагружение). При этом, напомним, что в качестве опасного напряжения для пластичных материалов типа малоуглеродистой стали берется предел текучести, а для хрупких материалов – предел прочности.

Учитывая, что 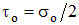, выражение (4.25) запишем в виде

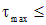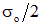(4.26)

Значительно сложнее провести расчет на прочность при двухосном и трехосном напряженных состояниях, когда касательные и нормальные напряжения напрямую не связаны друг с другом.

На практике поступают следующим образом. Высказывается та или иная гипотеза о причине разрушения материала, которая и проверяется на ограниченном количестве опытов с различными комбинациями действующих на гранях элемента напряжений.

На основании опытов для различных материалов построены многочисленные теории прочности. Ниже рассматриваются три классические теории. Прежде чем перейти к их рассмотрению, подчеркнем, что любому напряженному состоянию в точке тела можно поставить в соответствие эквивалентное напряженное состояние, описываемое главными напряжениями. При расчетах на прочность удобнее пользоваться именно главными напряжениями, поскольку их меньше, чем напряжений в системе координат x, y, z.

На рис. 4.1,б показан простейший пример, когда на гранях элемента действуют только нормальные напряжения. При отсутствии на гранях касательных напряжений эти нормальные напряжения являются главными.

Первая теория прочности. В этой теории максимальных нормальных напряжений предполагается, что разрушение (хрупкие материалы) или необратимые пластические деформации (пластичные материалы) при сложном напряженном состоянии наступает тогда, когда максимальное главное напряжение s₁ равно опасному напряжению s_о, которое определяется путем испытаний образцов при одноосном нагружении (растяжении или сжатии). При этом условие прочности запишется в виде

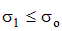(4.27)

В соответствии со строительными нормами получим:

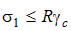(4.28)

Обратим внимание, что в неравенстве (4.28) в правой части записано не опасное напряжение, а предельное напряжение, рекомендуемое строительными нормами, которое равно произведению расчетного сопротивления на коэффициент условий работы. Это напряжение меньше опасного.

Недостатком данной теории прочности является то, что не учитывается влияние второго (а при трехосном напряженном состоянии и третьего) главных напряжений. Первая теория прочности хорошо согласуется с экспериментами для хрупких материалов, когда первое главное напряжение намного больше двух остальных.

Вторая теория прочности. В основу этой теории максимальных линейных деформаций положено предположение, что разрушение (хрупкие материалы) или необратимые пластические деформации (пластичные материалы) происходит при достижении максимальной линейной деформацией опасного значения 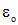, полученного из испытаний образца на одноосное нагружение.

При этом условие прочности запишется в виде

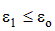(4.29)

Деформация 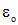определяется из опыта на одноосное растяжение. Выше было принято, что опасное напряжение для пластичных материалов равно пределу текучести 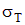, а для хрупких – пределу прочности 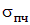. Для пластичных материалов вплоть до предела пропорциональности (его величина немного меньше предела текучести) справедлив закон Гука, то есть диаграмма деформирования линейна. Диаграммы напряжений при растяжении и сжатии хрупких материалов (бетон, кирпич, чугун) не имеют линейного участка. Сделаем допущение о линейном деформировании хрупких материалов. Тогда, опасную деформацию можно найти из закона Гука: 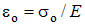. Выражение для максимальных линейных деформаций для трехосного напряженного состояния известно:

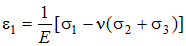
Условие прочности запишется в виде

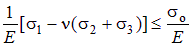
(4.30)

Сокращая на Е, получим условие, соответствующее второй теории прочности:

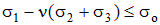
(4.31)

В соответствии со строительными нормами можно записать:

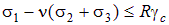
(4.32)

Можно заметить, что во второй теории прочности учитываются все три главных напряжения. Данная теория хорошо подтверждается для хрупких материалов в опытах на трехосное сжатие.

Третья теория прочности. Данная теория максимальных касательных напряжений основана на гипотезе, что причиной разрушения (хрупкие материалы) или необратимых пластических деформаций (пластичные материалы) являются максимальные касательные напряжения 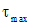. Условие прочности в данной теории записывается в виде

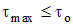(4.33)

Здесь 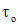– опасное касательное напряжение, определяемое из опытов на одноосное растяжение (сжатие) образцов. Учитывая, что t₀=s₀/2, а 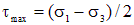, получаем условие по третьей теории прочности:

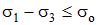(4.34)

В соответствии со строительными нормами можно записать:

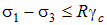(4.35)

Напомним, что R – расчетное сопротивление, а g_с – коэффициент условий работы.

Теория максимальных касательных напряжений подтверждается для пластичных материалов, одинаково работающих на растяжение и сжатие, в частности, для двухосного напряженного состояния. Недостаток этой теории состоит в том, что в ней не учитываются все главные напряжения.

Кроме трех рассмотренных теорий существуют и другие – энергетическая теория прочности, теория прочности Мора и т.д. Сведения об этих теориях можно найти в учебниках по сопротивлению материалов, список которых приведен в конце книги.

Дата добавления: 2018-10-27; просмотров: 1498; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!