Выводы и следствия двухфазного симплекс-метода.
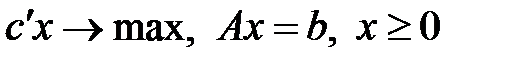(1)
С учётом симплекс алгоритма можно сделать для задачи (1) следующий вывод.
Пусть требуется решить каноническую задачу. Применим к ней двухфазный симплекс-метод. Возможны следующие исходы:
а)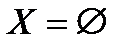 
, то есть ограничения задачи (1) несовместны, и у неё нет ни одного плана, а значит, нет оптимального плана (случай первой фазы);
б) у задачи будет построен 
– оптимальный базисный план (случаи 2 и 3 первой фазы и теорема 1 симплекс-метода);
в) будет доказана неограниченность целевой функции (случаи 2 и 3 первой фазы и выполнение теоремы 2 на второй фазе).
Других случаев для задачи (1) быть не может.
Следствие 1. Если у задачи (1) есть планы, то у неё обязательно есть и базисные планы.
Доказательство. Действительно, в этом случае возможен либо случай 2, либо случай 3 на первой фазе и оба они заканчиваются построением базисного плана.
Ч.т.д.
Следствие 2. Если у задачи (1) существует решение, то у неё обязательно будет и оптимальный базисный план.
Доказательство. Действительно, если не выполняется в случаях а) и в) вывода, то остаётся лишь случай б).
Ч.т.д.
|
|
|
Следствие 3. Для того чтобы у задачи (1) существовал оптимальный план необходимо и достаточно, чтобы её целевая функция была ограничена сверху на непустом множестве планов.
Доказательство. Необходимость. Если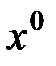 
– оптимальный план задачи (1), то целевая функция ограничена сверху числом 
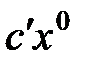и множество планов задачи непустое.
Достаточность. Пусть множество задачи (1) непустое и известно, что на этом множестве целевая функция ограничена сверху некоторым числом. Тогда возможен лишь исход б) вывода, то есть у задачи существует оптимальный план.
Ч.т.д.
Приведение задач к канонической форме. Табличная реализация симплекс-метода.
Двойственная задача. Взаимодвойственность.
|
|
|
В силу всеобщности рассмотрим каноническую задачу в виде:
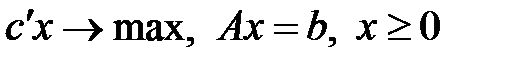(1)
все выводы справедливы в силу теоремы 4 для произвольной линейной задачи. По параметрам задачи (1) построим некоторую другую линейную задачу:
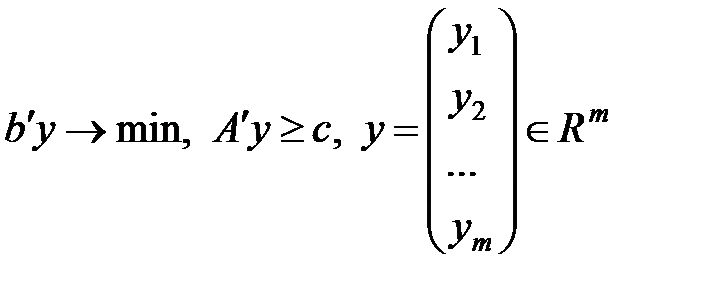(2)
Предположим, что у задачи (1) существует – оптимальный базисный план. Построим вектор
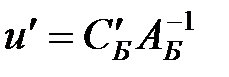(3)
Вектор 
называется вектором потенциалов для плана . Докажем, что он является оптимальным планом задачи (2).
Доказательство. Из (3) вытекает, что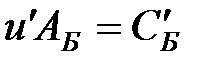 
и протранспонировав, получим 
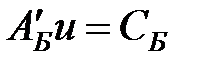(4)
В силу оптимальности выполняется условие
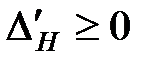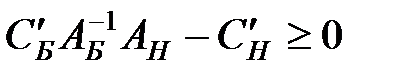или 
, или 
. Протранспонировав, получим:
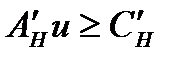(5)
Объединяем (4) и (5):
Сравнивая это соотношение с ограничениями задачи (2) видим, что они выполняются (только 
из них принимает вид равенств). Подсчитаем на векторе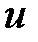 
значение целевой функции задачи (2):
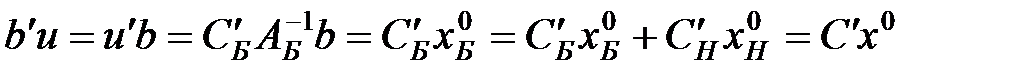(6)
|
|
|
Возьмём произвольный план задачи (2): 
и оценим на нём значение целевой функции:
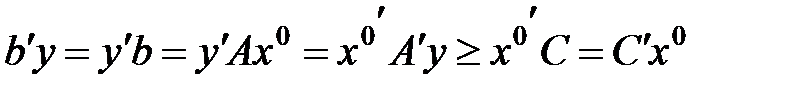
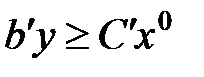(7)
Из (7) видно, что на произвольном плане задачи (2) целевая функция ограничена снизу числом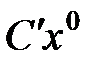 
, а на плане 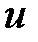эта нижняя граница достигается (6), следовательно, вектор 
.
Вывод: если 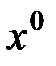– оптимальный план задачи (1), то соответствующий ему вектор потенциалов 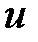– оптимальный план задачи (2).
Ч.т.д.
Задача (2) называется двойственной к задаче (1), а вектора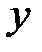 
– двойственными планами. Задачи (1) и (2) тесно связаны между собой.
Дата добавления: 2018-10-27; просмотров: 215; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!