Достаточное условие неограниченности. Алгоритм обратной матрицы.
Предположим, что на базисном плане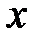 
не выполняется условие 
(4), тогда справедлива следующая теорема.
Теорема 2. Условие существования 
(10)
достаточно для того, чтобы 
.
Доказательство. Пусть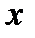 
– базисный план и выполняется условие (10). Будем строить 
, где вектор приращения 
выбираем по формулам 
(7) и 
(8). Тогда из 
(9) видно, что для 
.
Это означает, что для любого неотрицательного 
, 
будет планом и задачи (1), а из формулы приращения 
(3), тогда имеем
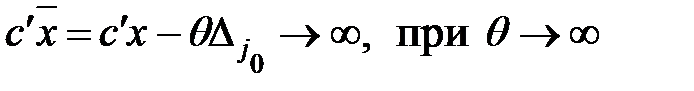(11)
то есть с ростом 
целевая функция будет неограниченно возрастать, оптимального плана задачи не будет и 
. Ч.т.д.
Выберем некоторый номер 
и вектор 
,
Лемма. Числа 
являются коэффициентами разложения вектора 
по базису в 
составленному из векторов 
(его координаты в этом базисе).
Доказательство.
(12)
Ч.т.д.
Итерация. Симплекс-метод (алгоритм).
Алгоритм :
При практическом использовании реализуется различные модификации симплекс метода: табличный, мультипликативный и так далее. Для реализации на ЭВМ наиболее удобна следующая:
|
|
|
1. Пусть дана каноническая задача со своими параметрами 
и пусть известна начальная обратная базисная матрица 
(обычно 
и тогда 
).
2. Вычисляем начальный базисный план: из основных ограничений 
получаем 
;
3. Строим вектор оценок базисного плана, используя (3): 
;
4. Проверяем критерий оптимальности 
(4). Если он выполняется, то записываем ответ 
– оптимальный базисный план, вычисляем 
. Если (4) не выполняется, то переходим к пункту 5;
5. Проверяем достаточное условие неограниченного роста (10): если оно выполняется, то записываем ответ (оптимального плана нет, целевая функция неограниченно растёт на 
), если не выполняется, то переходим к пункту 6;
6. Совершаем итерацию:
6.1. Находим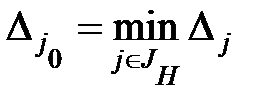 
6.2. Находим 
6.3. Находим 
6.4. Строим 
по формулам:
6.5. 
. И возвращаемся в пункт 2.
В этом алгоритме основную роль играет 
и лишь она на итерациях пересчитывается. Табличную модификацию симплекс-метода, изучим в лабораторном практикуме.
Конечность. Геометрическая интерпретация.
Определение.Вычислительный метод оптимизации будем называть конечным, если удаётся найти либо точное решение, либо доказать его отсутствие за конечное число операций на ЭВМ.
|
|
|
Определение. Каноническая задача 
(1), называется невырожденной, если у неё все базисные планы не вырождены ( 
).
В предыдущем пункте мы видели, что итерация совершается за конечное число операций. Поэтому для конечности метода нужно убедиться в конечном числе итераций.
Теорема 3. Симплекс-алгоритм для невырожденной канонической задачи конечен.
Доказательство. Пусть у задачи (1) построен начальный базисный план. Из пункта «Алгоритм обратной матрицы», ясно, что для доказательства конечности метода достаточно доказать конечность итераций. Если все базисные планы невырождены, то на каждой итерации 
.
Тогда при переходе от одного базисного плана к другому, то целевая функция строго возрастает на величину 
Таким образом, поскольку любому базисному плану будет соответствовать число 
, то в процессе итерации ни один базисный план не может встречаться дважды, а количество базисных планов задачи (1) конечно и не превосходит числа сочетаний 
. Действительно базисный план однозначно задаётся матрицей 
, а число различных подматриц 
можно выбрать конечное число 
точнее, не более чем 
(из n столбцов выбираем m), да ещё не любая подматрица невырожденная. Это и доказывает, что в результате итерации будет построен оптимальный базисный план, либо доказано его отсутствие.
|
|
|
Ч.т.д.
Если задача вырождена, то может оказаться, что на нескольких итерациях подряд 
(так как 
могут быть нулевыми) и если на итерациях это случится несколько раз подряд, то возникает опасность возвращения к уже встречавшемуся базисному плану. То есть в методе возможно зацикливание. Это редко встречается на практике, и к тому же разработана специальная модификация симплекс метода Бленда.
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
Геометрически множество планов канонической задачи (1), да и любой линейной представляет из себя некоторое многогранное выпуклое множество в 
(замкнутое или неограниченное), состоящее из внутренних точек, граней различной размерности, рёбер и угловых точек. Можно доказать, что базисному плану соответствует некоторая угловая точка множества 
и наоборот.
В симплекс-методе в результате итерации осуществляется переход от одной угловой точки по некоторому ребру к другой, причём таким образом, чтобы целевая функция увеличилась. В результате мы либо строим оптимальный план (оптимальными могут быть и несколько угловых точек (базисных планов) и точки рёбер и граней их соединяющих) либо находим бесконечное ребро, вдоль которого целевая функция неограниченно растёт. Других случаев быть не может.
|
|
|
Двухфазный симплекс-метод.
Дата добавления: 2018-10-27; просмотров: 173; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!