Дифференцирование сложной функции
Предположим, что функция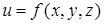 
определена в некоторой области D и имеет непрерывные частные производные 
, 
, 
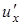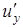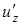, причем каждая из переменных 
, 
, 
является, в свою очередь, функцией переменной 
:
, 
, 
.
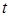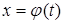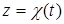Предположим также, что существуют и производные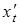 
, 
, 
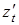. Тогда существует и производная по 
сложной функции 
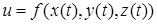, которая вычисляется по формуле
.
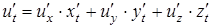В дифференциальной записи эту формулу можно переписать в следующем виде:
(10)
Если же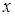 
, , зависят не от одной переменной, а от нескольких, например, 
, 
, 
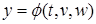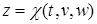, то после подстановки их в функцию 
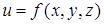в итоге получим некоторую функцию от трех переменных 
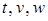. Тогда в предположении существования частных производных функции 
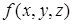и функций 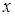, , по переменным 
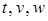можно вычислить и частные производные 
, 
, 
:
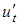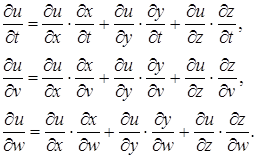
Для полного дифференциала функции справедлива формула, выражающая свойство инвариантности формы (первого) дифференциала:
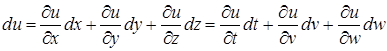. (11)
Если же задана функция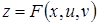 
, где 
зависят только от одного аргумента 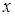, то есть является, по сути дела, функцией одной переменной 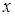, то можно говорить о полной производной 
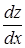, которая вычисляется по формуле:
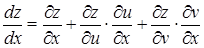. (12)
Пример 8. Найти частные производные по 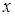и и полный дифференциал функции , если 
.
Решение. Так как
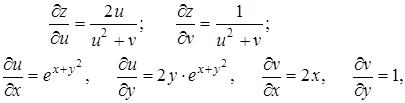
то
,
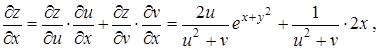
или
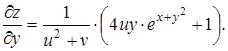
Поэтому полный дифференциал функции запишем в виде
,
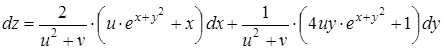откуда, после подстановки выражений для зависимых переменных, получим окончательное выражение для полного дифференциала заданной функции, как функции двух независимых переменных 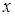и :
|
|
|
.
С другой стороны, полный дифференциал функции двух переменных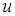 
и 
:
,
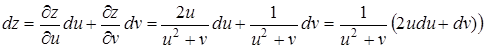а, в свою очередь,
.
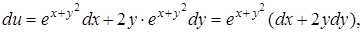
Тогда
.
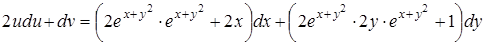
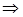
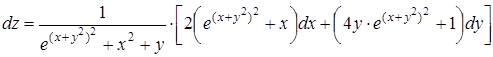Тем самым мы на практике подтвердили правильность формулы (11).
Пример 9. Найти полный дифференциал и частную и полную производные по 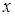функции , если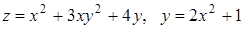 
.
Решение. Так как
,
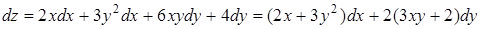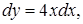
то
,
,
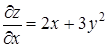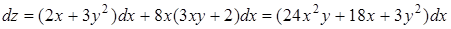откуда
.
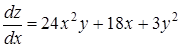Можно эту процедуру совершить наоборот: сначала найти частные и полную производные, а потом на их основе найти дифференциал функции.
Пример 10. Найти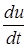 
, если 
, 
, 
.
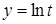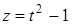Решение. Заданная функция зависит от трех переменных, каждая из которых является функцией одной переменной 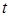. Поэтому и функция 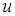является сложной функцией одной переменной 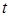. Для нахождения производной воспользуемся формулой (10), а для этого найдем все составляющие этой формулы:
, 
.
= 
.
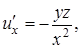
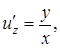
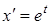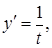
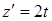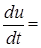
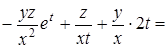
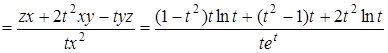Дата добавления: 2018-10-27; просмотров: 144; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!