Частные производные высших порядков
Пусть функция 
имеет в некоторой области D частную производную по одной из переменных 
(она называется также частной производной первого порядка). Тогда эта производная, сама являясь функцией тех же переменных, может иметь в некоторой точке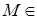 
D частные производные по той же 
или по любой другой переменной 
. Для исходной функции 
эти производные будут уже производными второго порядка (или вторыми частными производными). Производная второго порядка функции 
по аргументам 
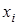и в точке 
обозначается одним из следующих символов:
Если 
, то частная производная второго порядка называется смешанной. Если 
, то частная производная второго порядка обозначается
Частные производные третьего порядка определяются как частные производные от частных производных второго порядка и т.д.
Следует отметить свойство смешанных частных производных:
Теорема. Если в точке 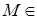D смешанные частные производные 
и 
непрерывны, то они равны между собой в этой точке, т.е.
,
или значение смешанной производной не зависит от того порядка, в котором производится дифференцирование.
Это свойство верно и для смешанных производных любого порядка.
Теорема. Если функция 
определена в некоторой области D иимеет в этой области всевозможные частные производные до 
го порядка включительно и непрерывные в D смешанные производные 
го порядка, то значение любой 
той смешанной производной не зависит от того порядка, в котором производятся последовательные дифференцирования.
|
|
|
Пример 5. Найти частные производные второго порядка функции 
.
Решение. Частные производные первого порядка для этой функции мы нашли раньше, рассматривая пример 1:
Найдем теперь частные производные от частных производных первого порядка, получим тем самым частные производные второго порядка заданной функции:
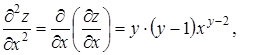
На примере убеждаемся, что смешанные частные производные не зависят от порядка дифференцирования, поэтому в дальнейшем будем находить только одну из них.
Дифференциалы высших порядков
Пусть функция 
определена в некоторой области D иимеет в этой области непрерывные частные производные первого порядка. Тогда она имеет и полный дифференциал 
:
,
который, в свою очередь, является некоторой функцией от тех же переменных. Если предположить существование непрерывных частных производных второго порядка для функции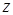 
, то в этом случае функция будет иметь непрерывные частные производные первого порядка, и можно будет говорить о дифференциале от этого дифференциала: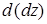 
, который называется дифференциалом второго порядка (или вторым дифференциалом) функции и обозначается 
.
|
|
|
Замечание. Приращения 
при этом рассматриваются как постоянные и остаются одними и теми же при переходе от одного дифференциала к следующему. Следовательно, дифференциалы любого порядка выше первого от независимых переменных равны нулю, т.е.
, 
. (7)
Поэтому, применяя правила дифференцирования и помня о равенстве смешанных производных по одному и тому же набору переменных, получим:
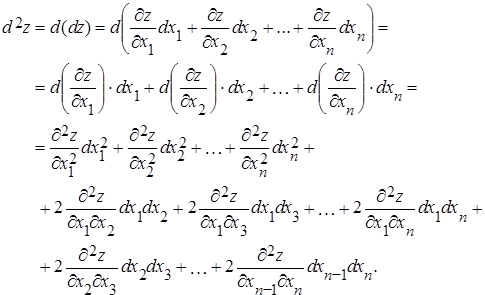
Здесь и далее 
, 
.
Аналогично определяются дифференциалы третьего 
, четвертого 
и т.д. порядков. Если определен дифференциал го порядка 
, то дифференциал 
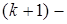го порядка определяется как полный дифференциал от дифференциала го порядка:
.
Сложность выражения для дифференциала зависит как от количества переменных, так и от его порядка. Поэтому проще запомнить символическое равенство
,
которое нужно понимать следующим образом: сначала многочлен, стоящий в скобках, формально по правилам алгебры возводится в степень, затем все полученные члены «умножаются» на 
, т.е. дописывается в числителе каждой дроби при 
, а после этого всем символам возвращается их значение производных и дифференциалов.
Например, если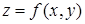 
, то
т.е.
(8)
|
|
|
таким образом,
(9)
и т.д.
Пример 6. Найти дифференциалы до третьего порядка включительно функции 
.
Решение. Для нахождения дифференциалов функции воспользуемся свойствами дифференциала, выраженными формулами (6) (дифференциал суммы, разности, произведения двух функций и т.д.) и определением дифференциала второго, третьего и т.д. порядков:
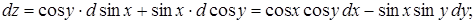
Теперь дифференцируем полученное выражение, помня, что дифференциалы независимых переменных есть константы, т.е. дифференциалы любого порядка выше первого от независимых переменных равны нулю (см. формулу (7)):
Дифференцируя третий раз, применяя те же правила, получим:
Здесь
.
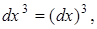
Для дифференциалов второго и третьего порядка данной функции мы получили бы те же самые выражения, если бы воспользовались для их нахождения формулами (8) и (9), т.е. если бы сначала нашли все частные производные нужных порядков, а потом подставили их в эти формулы. Проверьте и сравните.
Из полученных выражений для дифференциалов заданной функции мы можем теперь записать выражения для частных производных этой функции любого порядка, по любым независимым переменным, сопоставляя полученное с формулами (8) и (9), например:
, 
|
|
|
, 
.
Пример 7. Найти дифференциалы до третьего порядка включительно функции 
.
Решение. Так как все частные производные данной функции по переменной 
, начиная со второй, равны нулю, то здесь легко сразу воспользоваться формулами (3) и (4):
.
Дата добавления: 2018-10-27; просмотров: 388; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!