Примеры погрешностей округления некоторых чисел
Лабораторная работа № Ф-01-00.
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Введение
Целью лабораторного эксперимента, как правило, является определение значений физических величин и установление между ними количественных соотношений. Учебный эксперимент в процессе выполнения позволяет решить следующие задачи:
а) проиллюстрировать теоретические положения физики;
б) познакомиться с приборами;
в) приобрести опыт в проведении экспериментов.
"Приобрести опыт" означает научиться планировать эксперимент, ясно и кратко вести запись измерений, правильно обрабатывать результаты измерений, оценивать их точность, анализировать результаты эксперимента и правильно делать выводы. При выполнении лабораторных работ следует придерживаться общих правил.
1. Прежде всего необходимо познакомиться с основами теории изучаемого явления, а также с методикой эксперимента. Выяснить, какие физические законы положены в основу работы установки, проанализировать вывод рабочей формулы. Обратить внимание на упрощающие предположения, с учетом которых спланирован эксперимент.
2. Перед началом измерений полезно попрактиковаться в выполнении той или иной операции, разумеется, после изучения описания установки.
3. Даже при проведении однократных измерений следует хотя бы раз повторить опыт (без занесения результатов в протокол). Это позволит оценить правильность выполнения опыта и избежать грубых ошибок.
|
|
|
4. Все результаты следует немедленно записывать в протокол без какой-либо обработки. Не пользуйтесь черновиками, так как переписывание является источником дополнительных ошибок. Не проводите никаких, даже самых простых расчетов в уме. Например, если для получения правильных значений тока показания прибора надо делить на 2, то следует сначала записать показания прибора в «делениях» и лишь затем пересчитать их в амперы.
5. В протоколе эксперимента четко указывайте смысл буквенных обозначений всех используемых величин. Часто для этого достаточно указать их на схеме установки. Не забывайте указать единицы измерения.
И змерения и погрешности
Виды погрешностей .Измерением называется процесс сравнения измеряемой величины с однородной величиной, принятой за единицу измерения. В прямых измерениях искомое значение физической величины находят непосредственным отсчетом по шкале прибора. При косвенном измерении результат вычисляют по формулам, исходя из данных прямых измерений. Любое измерение осуществляется с определенной степенью точности, поэтому результат измерения содержит некоторую погрешность.
По характеру проявления погрешности разделяют на две основные группы.
|
|
|
1. Систематические погрешности сохраняют величину и знак от опыта к опыту. К ним относятся, например, погрешности, связанные с неправильным весом гирь, неточной разбивкой шкалы измерительных приборов и т. д. Эти погрешности, в принципе, могут быть исключены введением поправок, однако часто они остаются не выявленными.
2. Случайные погрешности обусловлены воздействием большого числа неконтролируемых причин, поэтому их величина и знак от опыта к опыту изменяются. Эти погрешности не могут быть учтены заранее, однако они подчиняются статистическим законам и их влияние может быть учтено и уменьшено при многократном повторении опыта.
Систематические погрешности, в принципе, опаснее случайных. Случайные погрешности обнаруживают себя в ходе эксперимента, в то время как при наличии скрытой систематической погрешности результат будет казаться вполне надежным, хотя на самом деле он весьма неточен.
Кроме названных погрешностей встречаются грубые ошибки, называемые промахами. Промахи могут появиться при неправильном отсчете, нарушении юстировки прибора, случайном воздействии значительного постороннего фактора и т. д. Результат, содержащий грубую ошибку, резко отличается от остальных, и его после проверки следует исключить.
|
|
|
По форме представления различают погрешности абсолютные, относительные и приведенные.
Отклонение измеренного значения величины x от ее истинного значения x0 называется абсолютной погрешностью:
Dx=x-x0
Абсолютная погрешность измеряется в тех же единицах, что и измеряемая величина (далее: ед. изм.).
Мерой точности результатов измерения является относительная погрешность, выраженная в долях:
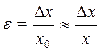 ,
,
или в процентах:
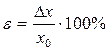 .
.
Приведенной погрешностью называется отношение абсолютной погрешности к некоторому нормированному значению. В качестве нормированного значения может быть выбран, например, предел измерения прибора на данном диапазоне.
В практике физического эксперимента погрешность измеряемой величины остается неизвестной. В противном случае истинное значение находилось бы простым введением поправки к измеренной величине. Методы теории погрешности позволяют лишь с некоторой вероятностью указать предельные значения погрешностей (случайных и выявленных систематических).
Погрешности однократных прямых измерений.. Если при повторных наблюдениях получаются одинаковые значения измеряемой величины, то повторять эксперимент не имеет смысла. В этом случае погрешность определяется точностью измерительного прибора. Если погрешность измерения на приборе (или в паспорте) не указана, она принимается равной цене наименьшего деления. Погрешность многих приборов определяется классом  точности. Значение класса точности g выражает предельную абсолютную погрешность, выраженную в процентах от верхнего предела измерений (на данном диапазоне)
точности. Значение класса точности g выражает предельную абсолютную погрешность, выраженную в процентах от верхнего предела измерений (на данном диапазоне)
|
|
|
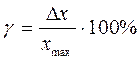 .
.
Предельная погрешность в этом случае может быть определена по формуле
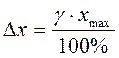 , ед. изм.
, ед. изм.
Например, предельная погрешность вольтметра на пределе измерения 10 В при классе точности 0,5 равна
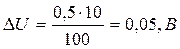
В погрешность прибора могут входить как систематические (неточная разбивка шкалы и т.д.), так и случайные (силы трения в оси и т.д.) погрешности. Однако поскольку при увеличении числа измерений точность прибора не возрастает, их следует рассматривать как систематические, хотя и неизвестной величины. Вероятность предельного значения приборной погрешности не указывается, но предполагается достаточно близкой к единице. Предельные погрешности приборов, часто употребляемых в лабораторной практике, указаны в табл. 1.
Таблица 1
Предельные погрешности приборов.
| Прибор или инструмент | Цена деления | Предельная погрешность |
| Измерительная линейка | 1 мм/дел | 1 мм |
| Штангенциркуль | 0,1 мм/дел 0,05 мм/дел | 0,1 мм , 0,05 мм |
| Микрометр | 0,01 мм/дел | 0,01 мм |
| Весы технические | - | 0,1 г |
| Весы аналитические | 0,1 мг/дел | 1 мг |
| Секундомер с ручным запуском | 0,1 с/дел | 0,3 с |
| Часы с секундной стрелкой | 1 с/дел | 1 с |
| Термометры | Т К/дел | Т, К |
| Приборы с классом точности g | C | g×Xmax /100»C/2 |
| Осциллографы (измерение амплитуды и длительности сигнала) | 0,1 Xmax (10% ) | |
| Цифровые приборы | - | (расчет по формулам) |
| Табличная величина | 0,5 единицы последнего разряда |
Погрешности многократных прямых измерений .Статистическую обработку результатов проводят в том случае, если при измерениях в тождественных условиях результат не повторяется. Рекомендуется следующий порядок обработки результатов.
1. Исключаются известные систематические погрешности.
2. За результат измерений принимают среднее арифметическое результатов серии n измерений.
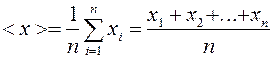 (1)
(1)
3. Определяются погрешности отдельных измерений
Dxi = xi - <x>
4. Вычисляется среднеквадратичное отклонение среднеарифметического значения
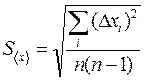 (2)
(2)
5. Доверительный интервал случайной погрешности (без учета знака) находят по формуле
Dx = ta,n-1 ×S<x> , (3)
где ta,n-1 - коэффициент Стьюдента для доверительной вероятности a и числа степеней свободы f=n-1 находят по табл.2. Доверительную вероятность обычно принимают a = 0,95.
6. Результат представляют в виде
x = <x> ± D x, ед. изм.,
a = ... , e =(D x/<x>)100% .
Примечания. 1. Если отдельное измерение резко отличается от остальных, то его следует отбросить как промах. Если погрешность какого-либо измерения велика, т.е.
 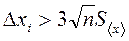 ,
то этот результат отбрасывается как промах. После его исключения расчет погрешности повторяется.
2. Если вычисленная случайная погрешность будет близка к погрешности прибора d, необходимо учесть совместное влияние обеих погрешностей. При отсутствии особых требований к точности рекомендуем упрощенную формулу для суммарного среднеквадратичного отклонения ,
то этот результат отбрасывается как промах. После его исключения расчет погрешности повторяется.
2. Если вычисленная случайная погрешность будет близка к погрешности прибора d, необходимо учесть совместное влияние обеих погрешностей. При отсутствии особых требований к точности рекомендуем упрощенную формулу для суммарного среднеквадратичного отклонения
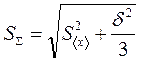 (4)
Суммарная погрешность определяется по формуле
Dx=ta,n-1×S<S> . (5)
Близкий результат дает суммирование не среднеквадратичных отклонений, а доверительных погрешностей (4)
Суммарная погрешность определяется по формуле
Dx=ta,n-1×S<S> . (5)
Близкий результат дает суммирование не среднеквадратичных отклонений, а доверительных погрешностей
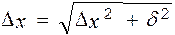 (6)
Если случайная погрешность будет значительно больше погрешности прибора, то последней пренебрегают. Если же, напротив, случайная погрешность невелика, то за погрешность измерения принимают погрешность прибора.
3. Проводить указанную выше статистическую обработку результатов можно только для такой серии, в которой разброс результатов обусловлен случайными причинами. Если же результаты различаются вследствие целенаправленного изменения условий опыта, то усреднение результатов такой серии не имеет смысла. (6)
Если случайная погрешность будет значительно больше погрешности прибора, то последней пренебрегают. Если же, напротив, случайная погрешность невелика, то за погрешность измерения принимают погрешность прибора.
3. Проводить указанную выше статистическую обработку результатов можно только для такой серии, в которой разброс результатов обусловлен случайными причинами. Если же результаты различаются вследствие целенаправленного изменения условий опыта, то усреднение результатов такой серии не имеет смысла.
|
Таблица 2
Коэффициенты Стьюдента
| Число степеней свободы f | Надежность a (доверительная вероятность) | |||||||
| 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 0,95 | 0,98 | 0,999 | |
| 1 | 1,00 | 1,38 | 2,0 | 3,1 | 6,3 | 12,7 | 32 | 640 |
| 2 | 0,82 | 1,06 | 1,3 | 1,9 | 2,9 | 4,3 | 7,0 | 32 |
| 3 | 0,77 | 0,98 | 1,3 | 1,6 | 2,4 | 3,2 | 4,5 | 13 |
| 4 | 0,74 | 0,94 | 1,2 | 1,5 | 2,1 | 2,8 | 3,7 | 8,6 |
| 5 | 0,73 | 0,92 | 1,2 | 1,5 | 2,0 | 2,6 | 3,4 | 6,9 |
| 6 | 0,72 | 0,90 | 1,1 | 1,4 | 1,9 | 2,4 | 3,1 | 6,0 |
| 7 | 0,71 | 0,90 | 1,1 | 1,4 | 1,9 | 2,4 | 3,0 | 5,4 |
| 8 | 0,71 | 0,90 | 1,1 | 1,4 | 1,9 | 2,3 | 2,9 | 5,0 |
| 9 | 0,70 | 0,88 | 1,1 | 1,4 | 1,8 | 2,3 | 2,8 | 4,8 |
| 14 | 0,69 | 0,87 | 1,1 | 1,3 | 1,8 | 2,1 | 2,6 | 4,1 |
| 19 | 0,69 | 0,86 | 1,1 | 1,3 | 1,7 | 2,1 | 2,5 | 3,9 |
| ¥ | 0,67 | 0,84 | 1,0 | 1,3 | 1,6 | 2,0 | 2,3 | 3,3 |
Примечание. Число степеней свободы равно числу независимых величин Dxi . При расчете S из n значений только n-1 значений будут независимыми, т.к. величины Dxi связаны одним уравнением:
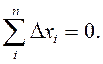 Поэтому в данном случае число степеней свободы будет равно f = n-1.
Поэтому в данном случае число степеней свободы будет равно f = n-1.
|
Пример. При измерении размера детали штангенциркулем получены следующие результаты:
| № п/п | xi , мм | Dxi мм | (Dxi)2, мм2 |
| 1 | 36,2 | 0,05 | 25×10-4 |
| 2 | 36,1 | -0,05 | 25×10-4 |
| 3 | 36,3 | 0,15 | 225×10-4 |
| 4 | 36,0 | -0,15 | 225×10-4 |
| 5 | 36,1 | -0,05 | 25×10-4 |
| 6 | 36,2 | 0,05 | 25×10-4 |
<x>=36,15 мм å (Dxi)2 = 550×10-4 мм
1. Результаты определения <x>, Dxi и å (Dxi)2 приведены в таблице. Таблица такого типа рекомендуется для удобства обработки результатов. Для вычисления <x> вместо формулы (1) рекомендуется эквивалентная формула, которая упрощает вычисления.
<x> = a + ( å(xi-a) )/n,
где a - любое “удобное” число, близкое к результату измерения. Если в нашем случае положить a = 36.0, то
<x> = 36,0 + (0,2+0,1+0,3+0,0+0,1+0,2)/6 = 36,15 мм..
Общая часть результатов a = 36.0 при этом не обрабатывается.
2. Находим среднеквадратичное отклонение по формуле (2)
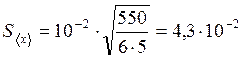 мм.
мм.
Здесь общий множитель 10-2 заранее вынесен из-под знака корня.
3. Определяем по табл.2 коэффициент Стьюдента для a = 0.95 и f=6-1=5: t(0,95;5) = 2.6 . Предельное значение погрешности (доверительный интервал) с вероятностью (надежностью ) 0.95 равен
Dx = 2,6×4,3×10-2 = 0,11 мм.
4. Так как полученная статистическая погрешность близка к погрешности штангенциркуля ( 0.1 мм ), необходимо внести уточнения по формуле (6). Окончательное значение погрешности
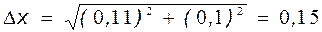 мм.
мм.
5. Результат запишется в виде
x = 36,15 ± 0,15 мм, a = 0,95.
Этот результат означает, что с вероятностью 0.95 истинное значение измеряемой величины лежит внутри интервала от 36.00 до 36.30мм.
Погрешности косвенных измерений . Часто оказывается, что искомая величина есть функция прямо измеряемых величин. Погрешность такой величины вычисляется через погрешности прямых измерений.
Случай одной переменной. Пусть искомая величина w есть некоторая известная функция прямо измеренной величины x , погрешность которой Dx, определена одним из указанных выше способов.
w = f(x)
Предполагая величину Dx малой, погрешность величины w можно найти как дифференциал функции:
D w = fx’(x) × D x (7)
где fx’(x) - производная функции f(x) по x.
Случай нескольких переменных. Пусть искомая величина w есть известная функция нескольких переменных x,y ..., погрешности которых Dx, Dy ... определены ранее одним из указанных выше способов:
w = f(x,y, ...)
Тогда правило дифференцирования дает формулы
Dwx = fx’(x)×Dx
Dwy = fy’(x)×Dy, (8)
. . . . . .
где fx’(x), fó’(x), ...- частные производные функции w = f(x,y, ...) по переменным x, y, и т. д. Величины Dwx, Dwy , ... нужно рассматривать как частные погрешности, возникающие за счет погрешности каждого аргумента в отдельности.
Однако нам известны не сами погрешности, а их предельные значения, которые пропорциональны среднеквадратичным отклонениям. Поэтому согласно правилу сложения дисперсий независимых величин необходимо суммировать не сами частные погрешности, а их квадраты.
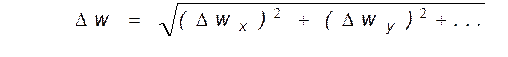 (9)
(9)
Непосредственное суммирование частных погрешностей без учета знака дало бы завышенный результат по сравнению с формулой (9). Однако маловероятно, что все погрешности величин x, y, z одновременно достигнут предельного значения с одним знаком. При использовании формулы (9) доверительная вероятность Dw оказывается та же, что и доверительная вероятность погрешностей Dx, Dy, ...
Рекомендуется следующий порядок расчета погрешностей:
1. Определяют погрешности прямых измерений одним из указанных выше способов.
2. Находят частные производные и определяют частные погрешности искомой величины по формуле (8).
3. Результирующую погрешность находят по формуле (9).
| Примечание. Если одна или несколько частных погрешностей окажутся заметно меньше ( 3 раза ) остальных, то в формуле их можно не учитывать без заметного ущерба точности. |
Пример. По результатам измерения диаметра цилиндра d=15,5±0,2 мм и высоты h=20,0±0,4 мм определить объём цилиндра V и погрешность его измерения DV.
Рабочая формула:
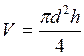
1. Находим объём цилиндра
V= 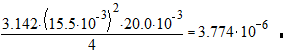 м3
м3
2. Находим частные погрешности
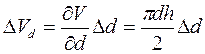
DVd= 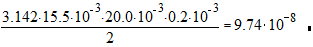 м3
м3
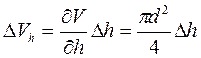
DVh= 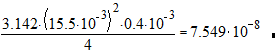 м3
м3
3. Находим результирующую погрешность
DV= 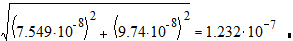 м3
м3
Ответ V=(3,77±0,12)×10-6 , м3
Примечание. Если аргументы входят в расчетную формулу только в виде произведений или частных в некоторой степени, то расчет погрешностей можно упростить. Пусть

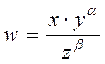 .
.
Прологарифмируем эту формулу
lnw=lnx+a×lny-b×lnz.
По правилу дифференцирования
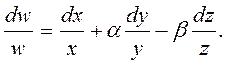
Но величины
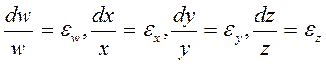
представляют собой относительные погрешности соответствующих величин. Поскольку каждая погрешность является независимой, то суммировать следует не конкретные приращения (с учетом знака), а их максимальные (доверительные) значения
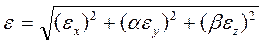
Таким образом, если какая-либо величина входит в расчетную формулу в виде множителя в степени a (включая отрицательные и дробные), то ее относительная погрешность дает вклад в общую погрешность (относительную) с этим множителем a.
В указанном случае рекомендуется следующий порядок расчета:
1. Находят относительные погрешности аргументов
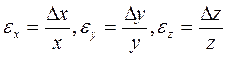 (10)
(10)
2. Производят суммирование относительных погрешностей (с учетом показателей степени) по формуле.
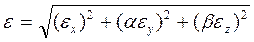 (11)
(11)
3. Находят погрешность величины w по формуле
Dw=w×e (12)
Пример. Определить указанным способом погрешности по данным предыдущего примера.
1. Определяем относительные погрешности определения диаметра цилиндра и его высоты:
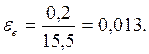
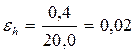
2. Находим относительную погрешность определения объема:
e = 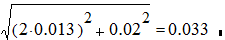
3. Абсолютная погрешность определения объема равна
Dw = 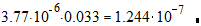 м3
м3
Легко видеть, что использование этого метода упрощает вычисление погрешностей. Обратите внимание, что поскольку диаметр входит в рабочую формулу в степени 2, то влияние его погрешности на погрешность результата удваивается.
Основные правила вычисления. Точность производимых в эксперименте вычислений должна соответствовать точности измерений. Рассмотрим два числа: 0.0204 и 0.02040 . Эти два числа имеют различную точность записи. Точность числа определяется числом значащих цифр. Значащей цифрой приближённого числа в десятичной записи называется любая цифра, кроме нулей, расположенных слева от первой ненулевой цифры. Так, в числе 0,02040 четыре значащие цифры. Первые два нуля не являются значащими и служат для указания разряда. Значащими являются цифры 2,0,4 и нуль, расположенный справа. Этот нуль указывает на численное значение разряда. В числе 0.0204 три значащие цифры. Разряд 10-5 в этом числе не определен.
Абсолютная погрешность записи числа равна половине единицы последнего приведенного в записи разряда. Так, число 0,0204 могло получиться округлением любого числа в интервале 0,0204±0,00005. Следует помнить, что относительная точность числа определяется числом значащих цифр, а не числом знаков после запятой. Так, числа 0,0204 (±0,00005) и 20,4 (±0,05) имеют одинаковую точность, отличаясь лишь множителем 103.
В больших числах нули справа могут служить как для указания значащих цифр, так и для определения разряда числа. Так, число 689 000 в указанной записи может иметь от трех до шести значащих цифр. Поэтому большие числа рекомендуется представлять в виде числа порядка единицы с соответствующей степенью числа 10. Указанное выше число следует записать в виде 6,89·105 , если оно имеет три значащие цифры, или 6,8900·105 , если оно имеет пять значащих цифр. Таким же образом следует записывать и малые числа: 0,00204 = 2,04·10-3 . Указанное правило облегчает вычисления с большими и малыми числами.
Таблица 3
Примеры погрешностей округления некоторых чисел
| Пример | Число значащих цифр | Погрешность округления |
| 3,1416 | 5 | 0,00005 |
| 3,14 | 3 | 0,005 |
| 0,1500 | 4 | 0,00005 |
| 0,015 | 2 | 0,0005 |
| 3 (целое) | ¥ | 0,000...0... |
Таблица 4.
Дата добавления: 2018-10-27; просмотров: 551; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
