По теме «Обыкновенные дифференциальные уравнения»
Определить тип дифференциального уравнения и найти его решение:
1) 

2) 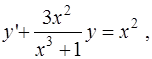

3) 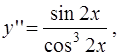


4) 
5) 

Решение задачи № 1
Важным теоретическим вопросом в теории дифференциальных уравнений является вопрос о том, насколько много решений имеет дифференциальное уравнение. Оказывается, что каждое дифференциальное уравнение имеет бесконечное множество решений, и поэтому приходиться ставить вопрос не о числе решений, а о том, как можно описать совокупность всех решений данного дифференциального уравнения. Ответ на этот вопрос дает теорема существования и единственности (см. [2] и [4]).
Во всех вариантах контрольной работы дифференциальное уравнение первого порядка можно представить в виде, разрешенном относительно первой производной:
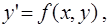 (1)
(1)
где функция 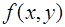 определена в некоторой области
определена в некоторой области  на плоскости
на плоскости 
Множество точек  на плоскости называется областью, если оно открыто и связно. Открытость
на плоскости называется областью, если оно открыто и связно. Открытость  означает, что вместе с каждой своей точкой множество
означает, что вместе с каждой своей точкой множество  содержит и некоторый круг с центром в этой точке. Связность
содержит и некоторый круг с центром в этой точке. Связность  означает, что любые две точки
означает, что любые две точки  можно соединить ломаной, целиком содержащейся в
можно соединить ломаной, целиком содержащейся в  . В частности, плоскость
. В частности, плоскость  является областью.
является областью.
Для уравнения (1) справедлива следующая теорема.
Теорема Коши о существовании и единственности решения.
Пусть функция 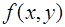 удовлетворяет двум условиям:
удовлетворяет двум условиям:
|
|
|
1) 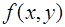 непрерывна в области
непрерывна в области  ;
;
2) имеет в  непрерывную частную производную
непрерывную частную производную 
Тогда решение задачи Коши для уравнения (1) с начальными данными  существует и единственно в том смысле, что существует единственная интегральная кривая уравнения (1), проходящая через точку
существует и единственно в том смысле, что существует единственная интегральная кривая уравнения (1), проходящая через точку 
Задача нахождения решения уравнения (1), удовлетворяющего начальному условию
 или, что то же самое,
или, что то же самое,  (2)
(2)
называется задачей Коши.
В нашем примере
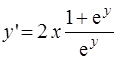 и функция
и функция  (3)
(3)
определена и непрерывна на всей плоскости  .
.
Вычислим частную производную  Для этого положим
Для этого положим  и будем рассматривать функцию
и будем рассматривать функцию

как функцию одной переменной  Применяя правила дифференцирования функции одной переменной, получим
Применяя правила дифференцирования функции одной переменной, получим


Здесь сначала постоянный множитель  вынесли из под знака производной по переменной
вынесли из под знака производной по переменной  а затем применили правило дифференцирования сложной функции.
а затем применили правило дифференцирования сложной функции.
Таким образом, частная производная  тоже определена и непрерывна на всей плоскости
тоже определена и непрерывна на всей плоскости  и, следовательно, теорема существования и единственности решения справедлива для уравнения (3) на всей плоскости.
и, следовательно, теорема существования и единственности решения справедлива для уравнения (3) на всей плоскости.
Анализ, проведенный выше, является основной частью решения задачи Коши, так как, используя программу типа Mathematiсa или зайдя на сайт www.wolframalpha.com (в режиме online и даже в пошаговой форме), Вы можете моментально получить решение.
|
|
|
Найдем общее решение дифференциального уравнения (3), не используя эти средства. Это уравнение с разделяющимися переменными (см. [2], [4] или [5]), так как оно имеет вид

где правая часть есть произведение функции  зависящей только от
зависящей только от  на функцию
на функцию 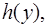 зависящую только от
зависящую только от 
В нашем уравнении (3)
 и
и 

Эти функции определены и непрерывны при всех 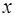 и
и  , причем
, причем 
Заменим  на
на  в уравнении (3):
в уравнении (3):

и разделим переменные, умножая обе части уравнения на выражение:

В результате получим уравнение

 (4)
(4)
которое называется уравнением с разделенными переменными.
Считая  известной функцией от
известной функцией от 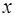 , равенство (4) можно рассматривать как равенство двух дифференциалов, а неопределенные интегралы от них будут отличаться на постоянное слагаемое.
, равенство (4) можно рассматривать как равенство двух дифференциалов, а неопределенные интегралы от них будут отличаться на постоянное слагаемое.
Интегрируя левую часть равенства (4) по  , а правую часть по
, а правую часть по  , получим
, получим
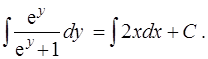 (5)
(5)
Интеграл 
Интеграл  вычислим с помощью подстановки
вычислим с помощью подстановки 
Учитывая, что  или
или 
получаем

Подставляя полученные выражения в равенство (5), найдем общий интеграл уравнения (3)
|
|
|
 (6)
(6)
В данном случае уравнение (6) можно разрешить относительно переменной  и получить общее решение дифференциального уравнения (3):
и получить общее решение дифференциального уравнения (3):

 и
и  (7)
(7)
Общее решение (7) дифференциального уравнения (3) – это однопараметрическое семейство решений, существование и единственность которых гарантирует теорема существования и единственности. Оно включает в себя все решения любой задачи Коши.
Для нахождения искомого частного решения подставим в общее решение начальные значения  и
и  Получим
Получим  ,
,  ,
, 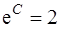 и
и 
При таком выборе 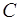 из общего решения (7) выделяется частное
из общего решения (7) выделяется частное

Ответ. Решением задачи Коши является функция  определенная на интервале
определенная на интервале 
Решение задачи № 2
Найдем решение уравнения
 (1)
(1)
Это линейное уравнение, т.е. уравнение вида

в котором предполагается, что функции
 и
и 
непрерывны в некотором интервале. Найдем его.
Функция  непрерывны при всех
непрерывны при всех 
Так как функция  имеет точку бесконечного разрыва
имеет точку бесконечного разрыва  то она непрерывна на двух интервалах
то она непрерывна на двух интервалах  и
и 
Мы выбираем интервал  потому что наше решение должно удовлетворять начальному условию
потому что наше решение должно удовлетворять начальному условию
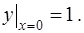 (2)
(2)
|
|
|
Точка 
Следовательно, дифференциальное уравнение (1) будем рассматривать в полосе  расположенной на плоскости
расположенной на плоскости 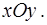 Тогда уравнение (1) удовлетворяет условиям теоремы существования и единственности решений (см. решение задачи №1 и [2], [4], [5]). Поэтому через каждую точку
Тогда уравнение (1) удовлетворяет условиям теоремы существования и единственности решений (см. решение задачи №1 и [2], [4], [5]). Поэтому через каждую точку  проходит единственная интегральная кривая уравнения, определенная на интервале
проходит единственная интегральная кривая уравнения, определенная на интервале 
Существуют различные способы нахождения общего решения линейного уравнения. Мы рассмотрим только один из них – метод Бернулли. Согласно этому методу будем искать решение  в виде произведения двух функций:
в виде произведения двух функций: 
Подставим функцию  в уравнение (1). Опуская аргумент
в уравнение (1). Опуская аргумент  в функциях
в функциях  и
и  и учитывая, что
и учитывая, что  получаем
получаем
 или
или 
Выбирая ненулевую функцию 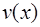 так, чтобы выражение, стоящее в скобках, обращалось в нуль, приходим к решению системы:
так, чтобы выражение, стоящее в скобках, обращалось в нуль, приходим к решению системы:

Уравнения (3) и (4) являются уравнениями с разделяющимися переменными в полосе  .
.
Разделим переменные в уравнении (3)
 или
или 
Интегрируя его, получаем

Положим постоянную  так как в качестве функции
так как в качестве функции  можно взять какое-либо ненулевое частное решение уравнения (3).
можно взять какое-либо ненулевое частное решение уравнения (3).
Вычисляя интегралы
 и
и 
имеем  и
и 
Найдем общее решение уравнения (4). Подставляя найденную функцию 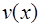 в уравнение (4), получим уравнение с разделяющимися переменными
в уравнение (4), получим уравнение с разделяющимися переменными
 или
или 
Разделяя переменные, найдем

Отсюда
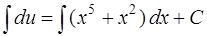 или
или 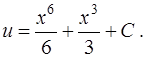
Общим решением уравнения (1) в полосе  будет функция
будет функция

определенная на интервале 
Используя начальное условие (2), найдем частное решение, интегральная кривая которого проходит через точку с координатами  и
и 
Для этого подставим  и
и  в выражение (5) и найдем значение постоянной
в выражение (5) и найдем значение постоянной  :
:


при котором из общего решения выделяется искомое частное.
Ответ. Решением задачи Коши (1),(2) является функция  определенная на интервале
определенная на интервале 
Решение задачи № 3
Найдем частное решение уравнения
 (1)
(1)
удовлетворяющее начальным условиям

 (2)
(2)
Данное уравнение является «простейшим» уравнением второго порядка, правая часть которого зависит только от независимой переменной  , т. е. уравнением вида
, т. е. уравнением вида

Предполагается, что функция  непрерывна в некотором интервале
непрерывна в некотором интервале  . Тогда для простейшего уравнения справедлива теорема существования и единственности решения (см. [2] и [4]).
. Тогда для простейшего уравнения справедлива теорема существования и единственности решения (см. [2] и [4]).
Для уравнения (1)  и с учетом начальных условий (2) мы выбираем интервал
и с учетом начальных условий (2) мы выбираем интервал  .
.
Тогда на плоскости  в интервале
в интервале 
 существует единственная интегральная кривая уравнения (1), проходящая через точку с координатами
существует единственная интегральная кривая уравнения (1), проходящая через точку с координатами  и
и  , при этом тангенс угла наклона касательной в этой точке равен нулю (геометрический смысл начальных условий (2)).
, при этом тангенс угла наклона касательной в этой точке равен нулю (геометрический смысл начальных условий (2)).
Найдем решение задачи Коши (1), (2).
Учитывая, что
 и
и 
проинтегрируем обе части уравнения (1) по переменной  . В результате получим
. В результате получим

Для вычисления интеграла сделаем замену переменной  .
.
Отсюда  ,
,  и
и


Таким образом,
 (3)
(3)
Найдем значение постоянной интегрирования  , используя начальное условие
, используя начальное условие  при
при  . Учитывая, что
. Учитывая, что  , получаем
, получаем

 и
и 
Подставим значение  в уравнение (3)
в уравнение (3)
 (4)
(4)
Интегрируя обе части уравнения (4) по переменной  , получим
, получим
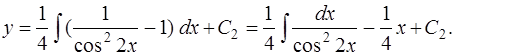
Для вычисления интеграла вновь сделаем замену переменной  и
и  .
.
Тогда

и, следовательно,

Найдем значение постоянной интегрирования  , используя второе начальное условие
, используя второе начальное условие  при
при  . Учитывая, что
. Учитывая, что  , получаем
, получаем
 и
и 
Отсюда искомое частное решение уравнения (1), удовлетворяющее начальным условиям (2), запишется в виде

Ответ. Решением задачи Коши (1),(2) является функция  определенная на интервале
определенная на интервале 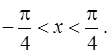
В задачах 4 и 5 даны линейные дифференциальные уравнения второго порядка с постоянными коэффициентами и со специальной правой частью.
Уравнение вида
 (1)
(1)
где  и
и  – вещественные числа, а
– вещественные числа, а  – функция непрерывная на некотором промежутке, называется линейным уравнением второго порядка с постоянными коэффициентами.
– функция непрерывная на некотором промежутке, называется линейным уравнением второго порядка с постоянными коэффициентами.
Функция
 (2)
(2)
называется функцией специального вида.
Комплексные числа  будем называть контрольными числами.
будем называть контрольными числами.


–многочлены степени  и
и  .
.
Функция специального вида (2) определена при всех 
Уравнение (1) называется неоднородным, если функция  не равна тождественно нулю. Если же
не равна тождественно нулю. Если же  то уравнение (1) принимает вид
то уравнение (1) принимает вид
 (3)
(3)
и называется однородным.
Если левые части однородного и неоднородного уравнений совпадают, то в этом случае однородное уравнение называется соответствующим данному неоднородному.
Имеет место следующее утверждение (см. [2], [4] и [5]).
Дата добавления: 2018-10-26; просмотров: 163; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
