Примерный вариант контрольной работы № 4
По интегральному исчислению в случае функции одной переменной
1. Вычислить следующие интегралы:
а) 
б) 
в) 
2. Вычислить площадь фигуры, ограниченной линиями  и
и 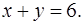
3. Вычислить объём тела, полученного вращением вокруг оси  плоской фигуры, ограниченной линиями
плоской фигуры, ограниченной линиями 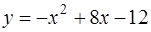 и
и 
4. Вычислить несобственный интеграл (или доказать его расходимость) 
Перед выполнением контрольной работы № 4 полезно ознакомиться с учебными пособиями [6] и [7], которые содержат необходимый теоретический материал и решения большого количества примеров. Задачи 2 и 3 взяты из учебного пособия [7].
Решение задачи № 1
В этой задаче требуется вычислить неопределенные интегралы, то есть найти функции, производные от которых равны подынтегральным функциям, стоящим в этих интегралах.
Основой вычисления неопределенных интегралов являются: таблица неопределенных интегралов основных элементарных функций; свойства неопределенных интегралов; теорема о замене переменной и формула интегрирования по частям (см. [1], [2] и [6]).
Решение примера а)
Представим данный интеграл в виде суммы двух интегралов

и воспользуемся теоремой о замене переменной для вычисления интегралов  и
и  .
.
В интеграле

сделаем замену переменной 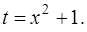 Тогда
Тогда 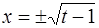 и, вспоминая определение дифференциала функции, находим, что
и, вспоминая определение дифференциала функции, находим, что
|
|
|

В результате интеграл  преобразуется к виду
преобразуется к виду

где  – произвольная постоянная.
– произвольная постоянная.
В данном случае переход в подынтегральном выражении от переменной  к переменной
к переменной 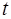 можно осуществить проще.
можно осуществить проще.
Так как в интеграле  имеется выражение
имеется выражение 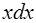 , то после выбора подстановки
, то после выбора подстановки  сразу вычислим дифференциал
сразу вычислим дифференциал
 . Откуда
. Откуда 
В результате интеграл  вновь преобразуется к виду
вновь преобразуется к виду

в последнем выражении необходимо подставить вместо  , то есть
, то есть

При определенном навыке использование теоремы о замене переменной при вычислении интеграла  можно оформить следующим образом.
можно оформить следующим образом.
Используя определение дифференциала функции и основные правила вычисления дифференциалов, преобразуем выражение

Подставляя это выражение в интеграл  , получаем
, получаем

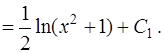

Здесь выражение  рассматривается как единый символ.
рассматривается как единый символ.
Этот способ оформления принято называть способом подведения части подынтегральной функции под знак дифференциала.
Замечание. Для проверки правильности полученного результата нужно убедиться, что производная найденной функции совпадает с подынтегральной функцией.


В интеграле  сделаем замену
сделаем замену  .
.
Тогда
|
|
|

и интеграл  преобразуется к виду
преобразуется к виду


где  – произвольная постоянная интегрирования.
– произвольная постоянная интегрирования.
Если воспользоваться способом подведения части подынтегральной функции под знак дифференциала, то, учитывая, что

получаем
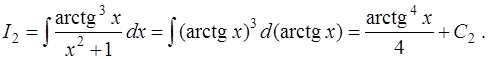
Здесь выражение  воспринимается как единый символ.
воспринимается как единый символ.
Ещё раз отметим, что, по существу, способ подведения части подынтегральной функции под знак дифференциала – это специфическая форма применения теоремы о замене переменной в неопределенном интеграле.
Ответ примера а) :  где
где  – новое обозначение для произвольной постоянной интегрирования.
– новое обозначение для произвольной постоянной интегрирования.
Решение примера б)
Для вычисления интеграла

воспользуемся теоремой о замене переменной и формулой интегрирования по частям.
Сначала сделаем замену переменной  Тогда
Тогда


и интеграл приводится к виду

К этому результату можно прийти и другим способом. После выбора подстановки  вычислим дифференциал
вычислим дифференциал 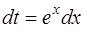 и перегруппируем функции, стоящие в подынтегральном выражении, следующим образом:
и перегруппируем функции, стоящие в подынтегральном выражении, следующим образом:

Для вычисления интеграла  применим формулу интегрирования по частям.
применим формулу интегрирования по частям.
Пусть 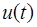 и
и  – две непрерывно дифференцируемые функции на некотором промежутке. Тогда имеет место формула
– две непрерывно дифференцируемые функции на некотором промежутке. Тогда имеет место формула
|
|
|

которая называется формулой интегрирования по частям.
Напомним, что  и
и 
В нашем случае положим

Тогда
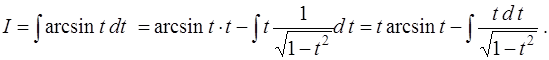
Интеграл  вычислим с помощью подстановки
вычислим с помощью подстановки 
Тогда  ,
,  и в результате получаем
и в результате получаем


Таким образом,


Ответ примера б) : 
Решение примера в)
В этом примере используются методы интегрирования тригонометрических функций (см. [1], [2] и [6]).
Для вычисления интеграла  применим следующие тригонометрические формулы
применим следующие тригонометрические формулы
 и
и 
Тогда


Последний интеграл  вычислим с помощью замены переменной
вычислим с помощью замены переменной 
Отсюда  и
и  В результате получаем
В результате получаем
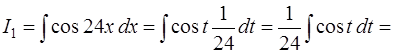

Ответ примера в): 
Решение задачи № 2
В этой задаче нужно вычислить площадь фигуры, ограниченной линиями 
Построим заданную фигуру (см. рис. 3). Найдем точки пересечения указанных в условии линий (параболы и прямой). Решим для этого систему уравнений

Она равносильна системе
 откуда
откуда 
Уравнение  задает прямую, которая проходит через две найденные точки c координатами
задает прямую, которая проходит через две найденные точки c координатами  и
и  .
.
Уравнение параболы 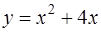 приведём к каноническому виду, выделяя полный квадрат по переменной
приведём к каноническому виду, выделяя полный квадрат по переменной  :
: 

Тогда каноническое уравнение параболы имеет вид
|
|
|

из которого видно, что парабола имеет осью симметрии вертикальную прямую  , вершину в точке
, вершину в точке  и ветви параболы направлены вверх (в направлении оси
и ветви параболы направлены вверх (в направлении оси  ).
).
Для того, чтобы найти площадь построенной фигуры, рекомендуют сначала составить выражение бесконечно малого элемента искомой площади, а затем проинтегрировать полученный результат в пределах изменения аргумента (см. [7]).
Обозначим бесконечно малый элемент площади через  .
.
Он равен площади прямоугольника, заштрихованного на рис. 3, со сторонами  и
и  , т.е.
, т.е.

Так как  и
и  , то
, то


Искомую площадь получаем, проинтегрировав полученный результат в пределах изменения переменной  от
от  до
до 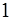 .
.
Тогда


Решение задачи № 4
В данной задаче нужно вычислить объём тела, полученного вращением вокруг оси  плоской фигуры, ограниченной параболой
плоской фигуры, ограниченной параболой  и прямой
и прямой 
Чтобы построить параболу, ее уравнение
 (1)
(1)
приведём к каноническому виду, выделяя полный квадрат по переменной  :
:
 ,
,
 . (2)
. (2)
Следовательно, парабола имеет ось симметрии  , вершину в точке
, вершину в точке  . Ветви параболы направлены вниз (в направлении, противоположном положительному направлению оси
. Ветви параболы направлены вниз (в направлении, противоположном положительному направлению оси  ). Кривая пересекает ось
). Кривая пересекает ось  в точках
в точках  и
и  . Заданная фигура заштрихована на рис. 4 (а). Вращая её вокруг оси
. Заданная фигура заштрихована на рис. 4 (а). Вращая её вокруг оси  , получим тело с полостью.
, получим тело с полостью.


Найдем объем  тела вращения. Для этого составим выражение бесконечно малого элемента объема
тела вращения. Для этого составим выражение бесконечно малого элемента объема  , а затем проинтегрируем полученный результат в пределах изменения аргумента
, а затем проинтегрируем полученный результат в пределах изменения аргумента
(см. [7]).
Бесконечно малый элемент искомого объема  равен объему кольцевого цилиндра с внешним радиусом
равен объему кольцевого цилиндра с внешним радиусом 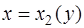 , внутренним радиусом
, внутренним радиусом 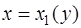 и высотой
и высотой  (см. рис. 4 (б), на котором выделен затененный цилиндр):
(см. рис. 4 (б), на котором выделен затененный цилиндр):
 (3)
(3)
Рассечём тело вращения плоскостью, перпендикулярной оси  . В сечении получим кольцо (рис. 4 (б)), которое является основанием нашего бесконечно тонкого кольцевого цилиндра. Чтобы определить внутренний
. В сечении получим кольцо (рис. 4 (б)), которое является основанием нашего бесконечно тонкого кольцевого цилиндра. Чтобы определить внутренний  и внешний
и внешний  радиусы этого кольца, вернемся к уравнению параболы. Из уравнения (2) найдём
радиусы этого кольца, вернемся к уравнению параболы. Из уравнения (2) найдём
 ,
,
следовательно,

Очевидно, что первая функция задает внешний радиус кольца, а вторая – внутренний, т.е.
 и
и 
Найдём бесконечно малый элемент искомого объёма по формуле (3):

 .
.
Для вычисления объёма тела вращения проинтегрируем полученный результат по переменной  . Тогда
. Тогда

Для вычисления интеграла сделаем подстановку  и используем теорему о замене переменной.
и используем теорему о замене переменной.
Найдем пределы интегрирования по переменной  : если
: если  , то
, то  если
если  , то
, то 
Так как  то
то  и в результате получаем
и в результате получаем

Решение задачи № 4
В этой задаче требуется исследовать интеграл 
Данный интеграл является несобственным, так как промежуток интегрирования  бесконечный. Напомним определение несобственного интеграла по бесконечному промежутку.
бесконечный. Напомним определение несобственного интеграла по бесконечному промежутку.
Пусть функция  определена при всех
определена при всех  и интегрируема на каждом конечном промежутке
и интегрируема на каждом конечном промежутке  . Рассмотрим предел
. Рассмотрим предел
 (1)
(1)
Его называют несобственным интегралом по бесконечному промежутку и обозначают символом
 . (2)
. (2)
Таким образом,

Если предел (1) существует и конечен, то говорят, что интеграл (2) существует или сходится. Если же рассматриваемый предел (1) не существует или бесконечен, то говорят, что несобственный интеграл (2) не существует или расходится.
В нашем случае


Для вычисления интеграла используем теорему о замене переменной в определенном интеграле, сделав подстановку 
Найдем пределы интегрирования по переменной  : если
: если 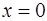 , то
, то 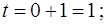 если
если  , то
, то 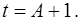
Так как  то
то  и в результате получаем
и в результате получаем

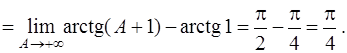
Следовательно, данный интеграл сходится и равен 
Контрольная работа № 3
Дата добавления: 2018-10-26; просмотров: 258; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
