Логические парадоксы – примеры и проблемы
Nbsp;
Тарасенко В.
Фрактальная логика
Линия состоит из множества точек; плоскость - из бесконечного множества линий; книга - из бесконечного множества плоскостей; сверхкнига - из бесконечного множества книг. Нет, решительно не так. Не таким more geometrico должен начинаться рассказ. Сейчас любой вымысел сопровождается заверениями в его истинности, но мой рассказ и в самом деле - чистая правда.
Х.Л. Борхес Книга песка
Содержание
Глава 1 Исторические предпосылки фрактальной логики
1.1 Математические “монстры” - примеры и проблемы
1.2 Логические парадоксы – примеры и проблемы
1.3 “Монстры” и парадоксы – неслучайные совпадения.
1.4 Исторический очерк фрактальной геометрии
1.5 Принцип дополнительности фрактальной геометрии
1.6 Парадоксы как фракталы. Фрактальная логика: обратная связь как модель “монстров” и парадоксов
1.7 Парадокс лжеца: логический формализм через понятие обратной связи.
| |
Глава 2 Логические ряды и логические фракталы
2.1 Определение логического ряда. Виды рядов.
2.2 Процедуры генерации логических рядов с помощью обратных связей. Прямая и обратная задача генерации логического ряда.
2.3 Операции с логическими рядами
2.4 Кортежи, масштабы и инварианты логических рядов. Самоподобие. Определение регулярного логического фрактала.
|
|
|
2.5 Формализм масштабного преобразования. Определение преобразованных логических фракталов.
2.6 Монады. Монадология.
2.7 Тезис о построении логического фрактала через два типа обратных связей
2.8 Количественные характеристики логических фракталов
Послесловие: проблемы и задачи фрактальной логики
Глава 1 Исторические предпосылки фрактальной логики
Математические “монстры” - примеры и проблемы
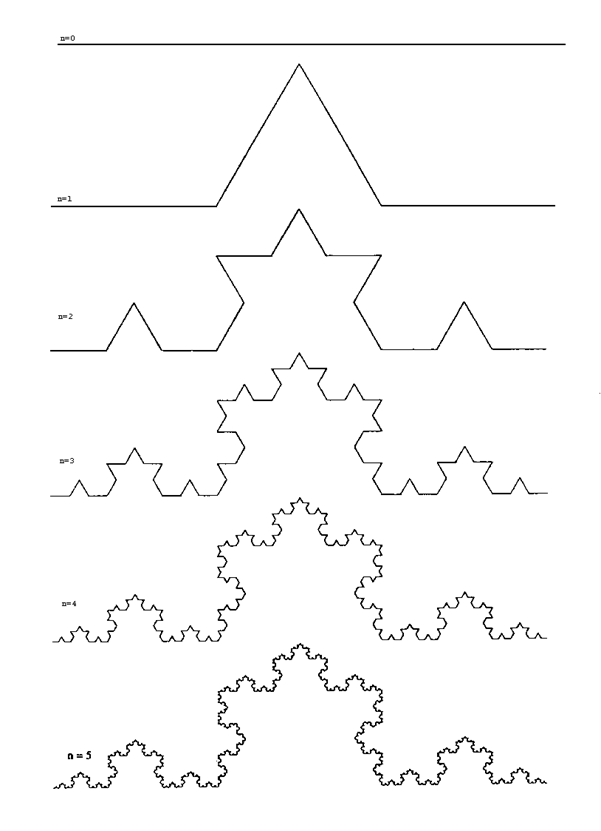
Рассмотрим построение триадной кривой, которую впервые исследовал в 1904 году шведский математик Хельге фон Кох (рисунок 1.1.1).
Возьмем прямолинейный отрезок длины 1. Назовем его затравкой. Разобьем затравку на три равные части длиной в 1/3, отбросим среднюю часть, и заменим ее ломаной из двух звеньев длиной 1/3 таким образом, чтобы средняя часть оказалась основанием равностороннего треугольника со стороной 1/3. Мы получили ломаную, состоящую из четырех звеньев с общей длиной 4/3 – так называемое первое поколение.
Для того чтобы перейти к следующему поколению кривой Коха, надо у каждого звена аналогично отбросить и заменить среднюю часть.
Соответственно, длина второго поколения будет равна 16/9, третьего – 64/27 и так далее.
Если продолжить этот процесс до бесконечности, то в результате получится триадная кривая Коха.
|
|
|
Рассмотрим свойства этой кривой.
Во-первых, эта кривая не имеет длины – как мы убедились, с увеличением числа поколений ее длина стремится к бесконечности.
Во-вторых, к этой кривой невозможно построить касательную – каждая ее точка является точкой перегиба (особой точкой или сингулярностью), в которой производная не существует - эта кривая не гладкая.
Длина и гладкость – фундаментальные свойства кривых, которые изучаются как евклидовой геометрией, так и неевклидовыми геометриями типа геометрий Лобачевского или Римана. На основании этих свойств развиваются методы анализа и преобразования геометрических фигур.
К триадной кривой Коха традиционные методы геометрического анализа оказались неприменимы. Поэтому, кривая Коха оказалась чудовищем – “монстром” среди гладких обитателей традиционных геометрий.
Одним из первых, кто досконально начал изучать “монстров” был Карл Вейерштрасс. Вслед за Бернардом Больцано, опубликовавшем в 1851 году книгу "Парадоксы бесконечности", он привел пример функции, графиком которой была негладкая кривая, обратив внимание на то, что понятие “непрерывная функция” и “непрерывная функция имеющая в каждой точке производную” не являются тождественными.
|
|
|
18 июля 1872 года в докладе Берлинской академии наук Вейерштрасс доложил пример негладкой непрерывной функции. Данная функция задается рядом:
W(x) =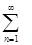 
аn cos (bnpx),
a<1, b>1, ab>1.
График этой функции (рис. 1.1.2) самоподобен, то есть, инвариантен (неизменен) при определенных преобразованиях координат (растяжения по абциссам в b раз и в 1/a раз по ординатам). В малом масштабе дублируются детали крупного масштаба, в результате этого можно говорить, что это функция никогда не сводится на малом отрезке к линии - она непрерывна, но не имеет дифференциала и производной. Функция имеет очень сложную “пилообразную” структуру - причем на “пилы” большего масштаба до бесконечности накладываются “пилы” меньшего.
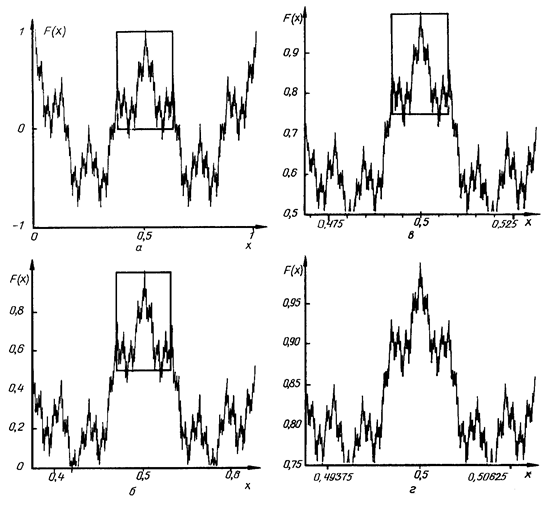
Рис 1.1.2 Функция Вейерштрасса при a=0,5 b=4 на различных масштабах: иллюстрация самоподобия[1]
Пример Вейерштрасса получил широкий отклик и потряс математиков. “Как интуиция может обмануть нас до такой степени?” - восклицал Пуанкаре. Бурбаки так описывает период появления “монстров”:
“...примеры кривых, не имеющих касательных, построенные Больцано и Вейерштрассом, положили начало патологическим явлениям в математике. В течение целого века мы видели столько чудовищ такого рода, что почувствовали некоторое пресыщение, и чтобы нас действительно удивить, надо было бы показать нам нагромождение самых нелепых уродств. У большинства математиков XIX в. чувство отвращения сменилось состоянием растерянности... надо было винить грубый и несовершенный характер нашей геометрической интуиции, и вполне понятно, что после этого она с полным правом была дискредитирована как средство доказательства”.
|
|
|
“Монстры” составили своеобразную альтернативу объектам и методам евклидовой геометрии. До конца XX века эта альтернатива носила скорее негативный, чем позитивный оттенок. “Монстры” не были другой геометрией, это были скорее “темные” и “запретные” зоны геометрического анализа в которых традиционные методы не работали.
Логические парадоксы – примеры и проблемы
"Из них же самих один стихотворец сказал: "Критяне всегда лжецы, злые звери, утробы ленивые". Свидетельство это справедливо".
Послание к Титу святого апостола Павла. Глава 1. Стих 12-13.
Как известно, логика оперирует с высказываниями – записанными с помощью знаков суждениями естественного или искусственного языка, которые имеют значения – сформулированные для данного высказывания логические содержания. Набор значений конечен. В случае классической двузначной логики этот набор - истина и ложь. Одно высказывание не может одновременно иметь несколько значений.
Высказывания можно формализовать – то есть записать на формальном языке и сформулировать логику высказываний – набор процедур и операций, которые преобразуют одни высказывания в другие или изменяют значения высказываний.
На этом предположении строится традиционная формальная логика, устанавливающая процедуры и операции над высказываниями.
Рассмотрим суждение естественного языка “Я лгу”. Преобразуем его в высказывание логики. Для этого проанализируем его содержание и интерпретируем логические значения.
Если мы предположим, что содержание высказывания “Я лгу” истинно, то его содержание указывает на то, что это высказывание ложно, следовательно, это высказывание является ложным, и его значение – ложь.
Если мы предположим, что содержание высказывания “Я лгу” ложно, то суждение “Я лгу” неверно. Следовательно, я говорю истину, и это высказывание является истинным. Его значение – истина.
Таким образом, одно и то же высказывание обладает двумя значениями одновременно.
Высказывание “Я лгу” – широко известный с древних времен пример семантического парадокса, иллюстрирующего противоречивость интерпретаций высказываний.
Одним из первых исследователей парадоксов был Зенон Элейский, занявший место в истории философии благодаря рассмотрению четырех парадоксов движения.
Рис.1.2.1 Зенон Элейский (430-495 до н.э.) и иллюстрация знаментитого парадокса "Ахилл и черепаха". Всего Зенонм было придумано более 40 апорий, направленных против бесконечности и движения.
В своих парадоксах Зенон пытался показать, что из определенного положения можно получить суждения, противоречащие друг другу. Следовательно, необходимо подвергнуть критике это положение.
Анализ парадоксов – любимая тема логических исследований XIX-XX веков, из которой выросло множество интересных работ по философии, основаниям математики, логическим теориям, искусственному интеллекту.
Парадоксы оказали колоссальное воздействие на литературу и беллетристику ХIХ-ХХ веков. Здесь можно упомянуть имена Л. Кэррола, Х.Л. Борхеса, Б. Касареса, Х. Кортасара, У. Эко, М. Павича.
Самой яркой работой на эту тему, на мой взгляд, является книга Дагласа Хофштадтера "Гёдель, Ешер, Бах"[2]. Главные герои книги – персонажи Зенона – Ахилл и Черепаха, постоянно попадают в бесконечные и парадоксальные ситуации. Между их диалогами обсуждаются проблемы логики, геометрии, биологии, нейрофизиологии, музыки и дзен-буддизма.
Кроме семантических парадоксов популярной темой исследований являлся анализ теоретико-множественных парадоксов, самым известным из которых был парадокс Рассела. Этот парадокс фиксировал противоречивость фундаментальной категории логики – категории множества.
Рис. 1.2.2 Бертран Артур Уильям Рассел (1872-1970). Портрет и шарж с формулировкой знаменитого парадокса. Рассел - автор огромного количества книг по философии, логике, основаниям математики. Нобелевскую премию получил по литературе.
Так же как и “монстры”, поражающие математиков, парадоксы поражали логиков. Они не вписывались в традиционные процедуры логического анализа и наводили на мысль о том, что в основаниях логики не всё благополучно.
1.3 “Монстры” и парадоксы – неслучайные совпадения.
Сопоставив историю исследований геометрических “монстров” и логических парадоксов, можно увидеть ряд удивительных совпадений.
Совпадения исторические.
Если начинать отсчет с мифических времен, то первым известным нам местом встречи монстров и парадоксов будет остров Крит.
"Все критяне лжецы" – сказал один критянин" – формулировка древнейшего парадокса.
Лжецы критяне, еще и потому, что якобы у них был выстроен лабиринт – топологический аналог геометрического "монстра" и дом мифического монстра Минотавра – чудовища с головой быка и туловищем человека. Минотавр живет в архитектурном «монстре». Первооткрывателем (или первостроителем) этого геометрического – архитектурного "монстра" следует признать Дедала – строителя лабиринта.
Случайно или нет совпадение места лабиринта и места рождения парадокса лжеца? Сказать сложно. Лично меня это совпадение удивляет и поражает. Когда совмещаешь эти вещи, то охватывает ощущение резонанса, соприкосновения с какой-то тайной зашифрованной в этом совпадении. Может быть, тайной рождения европейской культуры и цивилизации, европейского "линейного" мышления из "нелинейного" мифа. Я вернусь к этой теме в конце книги.
Мысленно перенесемся в другую эпоху и возьмем в качестве отправной точки 1903 год. В этом году Бертран Рассел пишет письмо Готлобу Фреге, впервые описывающее его знаменитый парадокс. Именно в этом году шведский математик Хельге фон Кох строит свои кривые и публикует их в следующем – 1904 году.
За тринадцать лет до этого Давид Гильберт в Кенигсберге исследует и обращает внимание научного сообщества на очередного “монстра” - кривую, построенную в 80 годах XIX века итальянским математиком и логиком Джузеппе Пеано. Приблизительно в это же время – в начале 90 годов, Георг Кантор исследует парадоксы в определении понятия “мощность множества”.
В 1912 году - через девять лет после 1903 года, поляк Вацлав Серпинский пополняет “монструарий” новыми фигурами - своими “салфетками” и треугольниками. На время перед первой мировой войной приходится расцвет полемики вокруг теоретико-множественных парадоксов в сообществе логиков.
В двадцатых-тридцатых годах ХХ века русский инженер адмирал А. Крылов применил функции без производных для моделирования процесса колебаний корабля: "монстры" постепенно стали приобретать физический смысл.
|
Рис 1.3.4 Фрагмент публикации Х. Коха "Une mйthode gйomйtrique йlйmentaire pour l'йtude de certaines questions de la thйorie des courbes planes", Acta Mathematica 30 (1906 г.),145-174
1.3.5 Давид Гильберт (1862 – 1943)
Великий немецкий математик, оставивший крупный вклад в теории инвариантов, основаниях геометрии, в логических основаниях математики. Его исследования "монстров" тесно переплетались с поисками непротиворечивых оснований геометрии.
1.3.6 Публикация Д. Гильберта (1890), анализирующая работы Пеано
1.3.7 Вацлав Францижек Серпинский (1882 - 1969)
Основные труды Вацлава Серпинского связаны с теорией множеств и ее приложением к топологии. Кроме этого, на русском языке известны работы Серпинского по теории чисел и арифметике.
1.3.8 Построение треугольника Серпинского
Рис. 1.3.9 Алексей Николаевич Крылов (1863-1945)
Всемирно известный кораблестроитель. Разработал схемы расчетов основных характеристик корабля – остойчивости и плавучести. Создал теорию килевой качки, заложил основы строительной механики, динамики и вибрации кораблей.
Совпадения биографические.
Георг Кантор – пример математика и логика, который в своем творчестве обращался как к анализу парадоксов, так и к построению и исследованию “монстров” причем на одном и том же примере. В 1883 году Кантор публикует свою работу “Ьber unendliche, lineare Punktmannigfaltigkeiten”, в котором демонстрирует пример построения “монстра” – множества точек, называемого сейчас множеством Кантора. Это множество образовано в результате бесконечного итерационного процесса, похожего на процесс построения кривой Коха (рис. 1.3.11). Кантор последовательно отбрасывал из отрезка единичной длины сначала среднюю часть, а потом средние части всех оставшихся фрагментов. Проделав эту процедуру бесконечное число раз, великий логик рассмотрел свойства получившегося множества точек – так называемой канторовой пыли. Кантор показал, парадоксальность этого “монстра”. Мощность получившегося множества точек оказалась равной мощности множества точек на отрезке.
В этом примере встретились парадокс и “монстр” – “монстр” оказался иллюстрацией парадоксального понятия мощности множества, воплощением непонятной бесконечности. Кантор пытается понять бесконечность и строит концепцию для ее описания.
Рис.1.3.10 Георг Фердинанд Кантор (1845-1918)
По выражению Гильберта, развив теорию множеств, Кантор построил рай для математиков. Первым ввел в математику понятие актуальной бесконечности, сопоставив ей математические объекты – трансфинитные числа. Построил теорию трансфинитных чисел, связав ее с теорией множеств. Ввел понятия мощности множества и подобия множеств.
Рис. 1.3.11 Построение канторовой пыли
Рис 1.3.12 Первая страница работы Кантора “Ьber unendliche, lineare Punktmannigfaltigkeiten” (1883)
Не случайным, с точки зрения изучения биографических совпадений, оказывается увлечение логикой Бернарда Больцано. В 1837 году Больцано пишет книгу "Попытка нового понимания логики", в которой он попытался ввести новую неформализованную "Про-Лейбницевскую" логику.
Попытки поиска оснований логики предпринимал и Джузеппе Пеано – автор кривой Пеано, исследовавший в 80-90 годах XIX века понятия числа. Пеано интересовался рекурсивными схемами – процедурами, с помощью которых можно определить понятие числа.
Работы Пеано оказали влияние на Бертрана Рассела, его взгляды периода "Принципов математики".
Совпадения социальные.
И “монстры” и парадоксы – это контрпримеры, противоречащие существующим на данный момент парадигмам в сообществе ученых, частные случаи, разрушающие хорошо выстроенные научные представления.
Есть совпадения в отношении научного сообщества к “монстрам” и парадоксам. Удивление, испуг, растерянность, заменялись запретами на их применение и попытками создать новую теорию, свободную от “монстров” и парадоксов – описать логически корректные и непротиворечивые основания математики.
Этот процесс был проанализирован Имре Лакатосом в его книге «Доказательства и опровержения». Лакатос назвал его “monster barring” - процессом “исключения монстров” - как некоторой позитивистской программы ухода от парадоксальности при исследовании геометрических и логико-математических объектов, построенных путем бесконечных рекуррентных процедур.
Книга «Принципы математики» Б. Рассела и А. Уайтхеда с этой точки зрения предстает как попытка исключения монстров, попытка найти непротиворечивые первые принципы, основания математики, свободные от рекурсий и бесконечных кругов, заселяющих логику "монстрами". Попытка, на взгляд Лакатоса, неудачная[3].
Совпадения операциональные: дискретность процедур.
Построение “монстров” и парадоксов можно представить как набор дискретных операций-алгоритмов, напоминающих рецепт. Сначала договариваются о каких-то правилах игры, а потом описываются конечные мыслительные или геометрические операции, исполнение которых приводит к тому, что появляется “монстр” или парадокс.
Совпадения самодостраивания и цикличности.
И “монстры” и парадоксы есть результат применения процедур к одному и тому же объекту и изменений этого объекта, исходя из состояния этого объекта. Парадокс – это самореферентное суждение, суждение о суждении. «Монстр» - самореферентная рекуррентная процедура.
В случае с парадоксами суждение начинает бегать по кругу – от “Высказывание истинно, значит оно ложно” к “Высказывание ложно, значит, оно истинно”. Мысль зацикливается и не может остановиться. При этом, суждение пытается обосновать себя самого – объектом анализа суждения становится само суждение, рождается новое значение, разрушающее присутствие старого значения. Это и есть “самодостраивание”: зацикливаясь, мыслительная процедура, выстраивает сама себя и рождает парадокс.
Аналогичный процесс запускается и при построении “монстров”. Фигуры Коха, Пеано или Серпинского не есть выстроенные объекты, а есть процессы самодостраивания – процессы бесконечных изменений одного и того же объекта.
“Монстр” есть выстраивание - циклический, постоянно возвращающийся процесс изменения. Если процесс итераций остановить, то “монстр” тут же превратится в обычную ломаную линию с конечным количеством особых точек.
Совпадения бесконечности.
Суждение, попав в логический круг, начинает вертеться в нем – значения не фиксируется, и меняется бесконечное число раз по циклу: “Суждение истинно значит ложно, суждение ложно значит истинно”.
Так же, до бесконечности, продолжается построение “монстра”.
Бесконечность присутствует как в изменении значений парадоксального высказывания, так и в итерациях “монстров”.
Бесконечность сводит с ума борцов с монстрами, являясь символом нелогичности и иррациональности.
Концептуальные совпадения
Есть несколько научных и философских концепций, обращающихся одновременно и к математическим монстрам, и к логическим парадоксам.
Во-первых, это теория хаоса и концепция сложности (complexity), синергетическая парадигма, которые приводят парадоксы в качестве результата "линейного" мышления. «Монстры» в этих концепциях - формы нового, "нелинейного" мира.
Во-вторых, это концепция автопоэзиса, бурно развиваемая сейчас философами, биологами и социологами, основателями которой считаются чилийские биологи и эпистемологи Умберто Матурана и Франциско Варела[4]. Франциско Варела в своих работах приводил монстры и парадоксы в качестве моделей саморазвивающихся, самодостраивающихся автопоэтических систем[5].
Многие статьи У. Матураны и Ф. Варелы присутствуют в ИНТЕРНЕТ. В качестве отправной точки можно сходить на сервер www.synergetic.ru, где присутствуют обзоры и библиография работ.
Наша задача состоит в том, чтобы выстроить совпадения математических "монстров" и логических парадоксов на концептуальном поле фрактальной геометрии.
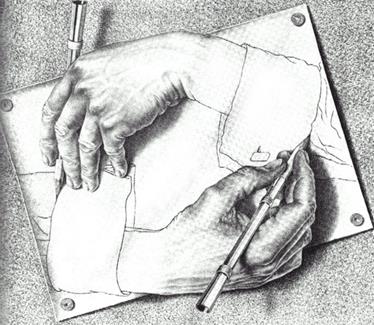
Рис 1.3.15 Иллюстрация бесконечного самодостраивания и цикличности: метафора автопоэзиса. М. Эшер. Руки.
1.4 Исторический очерк фрактальной геометрии
…( и что этот образ? не явь и не сон,
не заболеванье и не исцеленье,
а с криком летящая над колесом
мгновенная ласточка одушевленья)
тогда он и скажет себе: - Чудеса!
Не я ли раздвинул тяжелые вещи,
чтоб это дышало и было как сад,
как музыка около смысла и речи,
и было псалтырью, толкующей мне
о том, что никто, как она, не свободен, -
словами, которых не ищут в уме
делами, которых нигде не находят...
Ольга Седакова "Последний читатель"
"Почему геометрию часто называют холодной и сухой? Одна из причин заключается в ее неспособности описать форму облака, горы, дерева или берега моря. Облака - это не сферы, горы - не конусы, линии берега - это не окружности, и кора не является гладкой, и молния не распространяется по прямой. Природа демонстрирует нам не просто более высокую степень, а совсем другой уровень сложности. Число различных масштабов длин в структурах всегда бесконечно.
Существование этих структур бросает нам вызов в виде трудной задачи изучения тех форм, которые Евклид отбросил как бесформенные - задачи исследования морфологии аморфного. Математики, однако, пренебрегли этим вызовом и предпочли все больше и больше отдаляться от природы, изобретая теории, которые не соответствуют ничему из того, что можно увидеть или почувствовать."
Этими, ставшими уже популярными, словами американский математик Бенуа Мандельброт начинает свой всемирно известный бестселлер “The Fractal Geometry of Nature”[6].
Фрактальная геометрия, по Мандельброту это и есть настоящая геометрия природы, отличающаяся от традиционных геометрий, уводящих человека в царство безжизненных абстракций. Природа аморфна и причудлива.
Фрактал - форма природного хаоса, форма аморфного, форма бесформенного, приближающая взгляд и ум человека к природе.
Термин "фрактал" предложен Мандельбротом. Вот что пишет он сам по этому поводу в разделе “Фрактал” и другие неологизмы” во введении к своей книге “Фрактальная геометрия природы”[7]:
"Я создал термин фрактал от латинского прилагательного fractus. Соответствующий латинский глагол frangere означает "разрывать, прерывать": создавать нерегулярные фрагменты. Это, следовательно, имеет (подходящее для нас!) значение дополнительное к термину "фрагментированный" (как и к фракция ( fraction ), рефракция ( refraction )), fractus также "нерегулярный", оба значения сохраняются в термине fragment.
Правильнее поизносить - frac'tal - с ударением таким же, как и в слове fraction.
Сочетание “фрактальное множество” (fractal set) будет определена строго, но сочетание “природный фрактал” (nature fractal) будет подано свободно - для определения природных примеров, которые полезно репрезентировать с помощью фрактальных множеств. Например, броуновская кривая - это фрактальное множество, а физическое броуновское движение - это природный фрактал.
(Поскольку алгебра происходит от Арабского jabara = “связывающего вместе”, фрактал и алгебра стоят в этимологических оппозициях!)
Обычно, в моих путешествиях по вновь открытой или заново определенной территории, я часто перемещался под влиянием права на присваивание имени поворотным пунктам этой территории. Как правило, тщательно созданный неологизм представляется более лучшим, чем добавление новый морщина к уже затасканному термину.”
Мандельброт рассматривает математические аналоги природных форм и уточняет представление о фракталах – особых геометрических множествах, форма которых принципиально отличается от традиционных геометрических форм типа точки, линии и плоскости.
В качестве примера фракталов Мандельброт рассмотрел множества Жюлиа Мандельброта на комплексной плоскости.
В основе построения этих множеств лежит рекуррентная процедура - процесс итерации z®f(z,c), где z -комплексная переменная, c - комплексная константа, f - нелинейная функция.
Если x и y - координаты плоскости, то переменная z=x+iy, константа c=p+iq, а, например, нелинейную функцию можно выбрать такую: f(z,c)=z*z+c.
Тогда если c=0, то все точки z делятся на три класса:
1.|z|<1 => аттрактор точки z - это точка (0,0),
2.|z|=1 => точка z останется на окружности радиуса 1,
3.|z|>1 => аттрактор точки z - бесконечность,
Если c - не нуль, то возникает аттрактор, отличный от нуля.
Аттракторы - это центры притяжения, которые ведут борьбу за влияние на плоскости; любая начальная точка либо в течение процесса приходит к тому или иному аттрактору, либо лежит на границе и не может принять определенного решения. С изменениями параметров меняются и области влияния аттракторов, а вместе с ними и границы.
Множества Жюлиа и Мандельброта строятся рекурсивно при помощи различных функций F и G, позволяющих перейти от k-той точки на плоскости к (k+1)-ой точке по следующему закону:
x(k+1)=F(x(k), y(k),p),
y(k+1)=G(x(k), y(k),q),
где p и q - параметры, которые считаются постоянными в течение каждой итерации (x(0),y(0))->(x(1),y(1))->...->(x(k),y(k))->... В качестве функций F и G можно рассматривать различные нелинейные функции. Если плоскость, состоящая из всех пар (x,y), рассматривается при фиксированных p и q, то получаются так называемые множества Жюлиа. Если, напротив, фиксируется начальная пара значений (x,y) и прослеживается ее судьба при различных значениях параметров p и q, то получаются изображения, называемые множествами Мандельброта.
Вот что писал великий английский физик и математик Роджер Пенроуз по поводу фрактального множества Мандельброта:
“Доводилось ли вам когда-нибудь видеть картины, нарисованные компьютером, - объекты, известные под названием множеств Мандельброта? Впечатление такое, как будто вы отправляетесь в путешествие в какой-то далекий мир. Вы включаете свое чувствительное устройство, видите невероятно сложную конфигурацию с множеством всевозможных деталей и пытаетесь понять, что это такое. Вы можете вообразить, что перед вами какой-то необыкновенный ландшафт или, быть может, живое существо, облепленное со всех сторон крохотными детенышами, очень похожими на породившее их создание, но всё же несколько отличающееся от него. Весьма искусная и впечатляющая картина!
И всё же, даже глядя на уравнения, никто не имел ни малейшего представления о том, что они могут порождать структуру такого типа. А ведь эти ландшафты - не плод чьего-то разыгравшегося воображения: все видят одну и ту же картину.
Вы исследуете нечто с помощью компьютера, но это ничем не отличается от исследования, проводимого с помощью обычной экспериментальной техники.”
Мандельброт демонстрирует методологию описания множеств, полученных с помощью рекуррентных процедур.
В качестве качественного инварианта описания он применяет понятие самоподобия, подразумевающее подобие фрагмента множества, полученного бесконечной рекуррентной процедурой, всему множеству.
Рис. 1.4.1 Бенуа Мандельброт (род. 1924)
Автор термина "фрактал" и основоположник фрактальной геометрии.
|
а) б)
в) г)
д) е) Рис 1.4.2 а)-е) Фрагменты множества Мандельброта при различных масштабах. Фрагмент в рамке показан на следующем (по буквенному обозначению) рисунке. Фрагмент в е) напоминает по форме а).
|
Для количественного описания фрактальных множеств Мандельброт предложил использовать понятие размерности фрактального множества.
В обычном понимании размерность геометрического множества есть число измерений, с помощью которых можно задать положение точки на геометрическом объекте.
В свое время бурные дискуссии вызвал переход в “многомерие” - от плоскостей с размерностью два и евклидовых пространств с размерностью три, к менее представляемым n-мерным абстракциям. Достаточно сложно себе представить четырех, пяти или шестимерное пространство.
Сходная ситуация, на наш взгляд, складывается и в связи с освоением концепции фрактала.
Переход от «линейного мышления» к «фрактальному» сопряжен с введением новых интерпретаций размерности - числа измерений предметов.
Фрактальная геометрия заставляет мыслить в понятиях “дробномерия” - дробных измерений, или даже “дробномирия”.
Вот что пишут Ю.А.Данилов и Б.Б.Кадомцев в известной статье "Что такое синергетика?"[8]:
Мандельброт предложил использовать в качестве меры «нерегулярности» (изрезанности, извилистости и т. п.) определение размерности, предложенное Безиковичем и Хаусдорфом. Фракталь (неологизм Мандельброта) - это геометрический объект с дробной размерностью Безиковича-Хаусдорфа...
...Размерность Безиковича-Хаусдорфа всегда не меньше евклидовой и совпадает с последней для регулярных геометрических объектов (для кривых, поверхностей и тел, изучаемых в современном учебнике евклидовой геометрии). Разность между размерностью Безиковича-Хаусдорфа и евклидовой - «избыток размерности» - может служить мерой отличия геометрических образов от регулярных. Например, плоская траектория броуновской частицы имеет размерность но Безиковичу-Хаусдорфу больше 1, но меньше 2: эта траектория уже не обычная гладкая кривая, но еще не плоская фигура....
...Под фракталом, подразумевался некий сильно изрезанный, геометрический объект, который являлся, например уже не точкой, но еще не гладкой линией, или уже не линией, но еще не плоскостью.”
Мандельброт специально нашел такое определение размерности (размерности по Хаусдорфу и Безиковичу), которое бы в частном случае соответствовало нашим представлениям о классических целых размерностях, а в общем случае позволяло вводить и измерять фрактальные предметы.
Для уточнения понятия размерности рассмотрим множество S точек в некотором евклидовом пространстве.
Будем покрывать это множество по очереди отрезками прямой, квадратами, кубами. Для этого выберем функцию покрытия h(d) = g(d)dd, которая при d=1 соответствует прямолинейным отрезкам, при d=2 квадратам, при d=3 - кубам. g - это геометрический коэффициент равный в нашем случае единице.
Рассмотрим меру множества Md=Sh(d). Мера – это общее понятие для таких понятий как длина, площадь и объем, которая работает "в зазорах" между этими понятиями.
При d®0 мера Md равна нулю или бесконечности в зависимости от выбора d-размерности меры. Например, при покрытии фрагмента плоскости отрезками (d=1) мера равна бесконечности так как длина плоскости бесконечна - поверхность нельзя покрыть конечным числом отрезков, чья длина стремится к нулю. При покрытии фрагмента плоскости кубиками (d=3), мера стремится к нулю - объем плоскости равен нулю. Однако, при d=2 мера плоскости стремится к конечной величине. Этой мерой служит площадь исследуемого нами фрагмента плоскости.
При покрытии фигуры Коха (рис.1.1.1) отрезками (d=1), мера (длина фигуры) стремится к бесконечности. При покрытии фигуры Коха квадратами (d=2) мера (площадь фигуры) стремится к нулю. Этот факт дает основание предположить, что между d=1 и d=2 должно существовать значение d, при котором мера меняет свое значение с нуля на бесконечность.
Размерность Хаусдорфа-Безиковича D множества S есть критическая размерность, при которой мера Md меняет своё значение с нуля на бесконечность:
Md=Sg(d)dd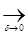 
0 при d>D; Md=Sg(d)dd 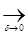¥ при d<D.
В случае с плоскостью, размерность Хаусдорфа-Безиковича равна двум. В случае фигуры Коха эта размерность не является целой и является фрактальной. Мера фигуры Коха не является длиной и площадью, а находится между ними.
Для определения размерности сложной фигуры на евклидовой плоскости (береговой линии, кластера), ее покрывают набором квадратов со стороной l®0, и при различных l подсчитывают число квадратов N(l). Далее ищется степенная функция меры таким образом, чтобы она была конечной при каком-то показателе степени. Для этого в двойных логарифмических координатах строится зависимость числа квадратов, покрывших фигуру, от длины сторон этих квадратов. Получается график, похожий на график зависимости длины береговой линии от функции выбранного шага (рис. 1.5.2). По углу наклона этого графика определяется фрактальная размерность.
Размерности можно вводить и по-другому. Будем покрывать изучаемое множество в p-мерном пространстве кубиками с ребром e. Кубику с номером i сопоставим вероятность Pi, с которой в него попадают точки множества. Далее можно ввести набор величин Dq называемых обобщенными размерностями, по формуле:
Dq = 
,
где суммирование ведется по всем кубикам покрытия.
При разных q возникают разные виды размерностей, характеризующих исследуемое множество - степень упорядоченности точек в пространстве.
Теория размерности – область математики, активно разрабатываемая в работах А. Н. Колмогорова, А. Реньи, Ф. Хаусдорфа.
1.4.3 Феликс Хаусдорф (1868 - 1942)
Автор оригинальных трудов по теории множеств, топологии, функциональному анализу. Предложил понятие меры и размерности, которое использовал Мандельброт для количественного описания фракталов. В 1942 году покончил жизнь самоубийством, узнав о предстоящей отправке своей семьи в гитлеровский концлагерь.
Рис. 1.4.4 Андрей Николаевич Колмогоров (1903 - 1987)
Великий советский математик. Получил фундаментальные результаты в теории множеств, теории меры, используемые в хаотической и фрактальной динамике.
Рис. 1.4.5 Альфред Реньи (1921 - 1970)
Внес большой вклад в теорию размерностей и теорию множеств. Во фрактальной геометрии и мультифрактальном анализе активно используется понятие обобщенной размерности, введенное Альфредом Реньи.
Дата добавления: 2018-10-26; просмотров: 424; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!