Производная степенной функции
Степени и корни
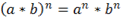
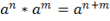
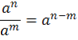
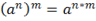
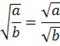
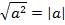
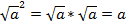, если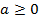 
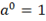
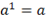
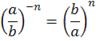
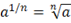
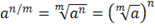
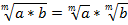
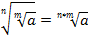
Решение квадратных уравнений
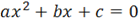
Если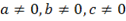 
, то квадратное уравнение полное, решается по формулам дискриминанта:
,
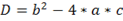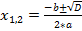если D>0, то 2 решения
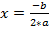если D=0, то 1 решение
Если D<0, то решений нет.
Если с=0: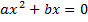 
, то квадратное уравнение неполное, решается разложением на множители левой части. Выносим Х за скобки:
,
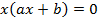произведение равно нулю, когда один из множителей равен нулю:
x=0 или ax+b=0.
Если b=0, то квадратное уравнение неполное:
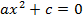
Для его решения выражаем 
:
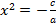, если 
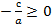, то решение существует, и находится:
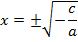
Формулы сокращенного умножения
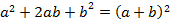
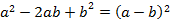
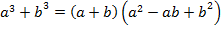
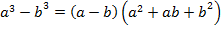
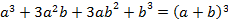
Тригонометрия
Простейшие формулы
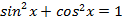
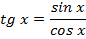
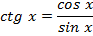
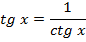
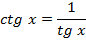
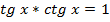
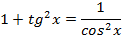
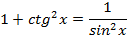
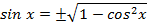
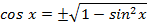
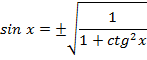
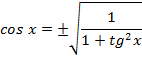
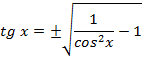
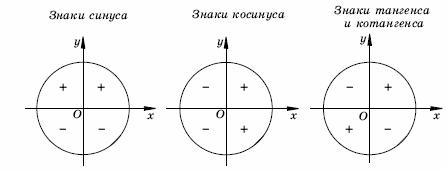
Знаки тригонометрических функций по четвертям
Тригонометр
Значения тригонометрических функций для углов первой четверти
| 0 |  ;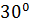 
|  ; 
|  ; 
|  ; 
| |
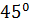
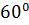
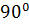
| Sin | 0 | 
| 
| 
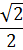
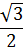
| 1 |
| cos | 1 |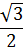
|
|
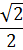
| 0 |
| tg | 0 |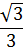 
| 1 |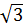 
| 
|
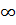
| ctg |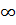
|
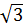
| 1 |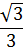
| 0 |
Формулы двойного аргумента
sin2x = 2sinx cosx
cos2x = cos2x - sin2x = 2cos2x - 1 = 1 - 2sin2x
Формулы сложения аргументов
sin(α+β)=sinαcosβ+cosαsinβ
cos(α+β)= сosα cosβ - sinα sinβ
sin(α-β)=sinαcosβ-cosαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
Формулы суммы тригонометрических функций
| sinα + sinβ | = 2sin | α + β | ∙ cos | α - β |
| 2 | 2 |
| cosα + cosβ | = 2cos | α + β | ∙ cos | α - β |
| 2 | 2 | |||
Формулы разности тригонометрических функций
| sinα - sinβ | = 2sin | α - β | ∙ cos | α + β |
| 2 | 2 |
| cosα - cosβ | = -2sin | α + β | ∙ sin | α - β |
| 2 | 2 |
(вместо заучивания формул приведения лучше освоить «лошадиное правило»)
Решение простейших тригонометрических уравнений
Уравнение вида sin x = a
Имеет решение только, если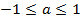 
Школьная форма записи (рекомендуется, если надо записать только ответ в такой форме и далее ничего с ним не делать и никак не использовать):
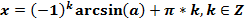
Альтернативная форма записи (рекомендуется во всех остальных случаях):
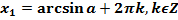
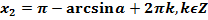
Значения для арксинусов берем из таблицы
(если значение нетабличное, но удовлетворяет условию существования решения, записываем просто: arcsin(правая часть уравнения)):
| a | arcsin a | |||
| град. | рад. | |||
| – 1 | – 90° | –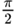 
| ||
– 
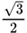
| – 60° | –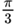 
| ||
– 
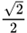
| – 45° | –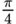 
| ||
– 
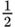
| – 30° | –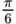 
| ||
| 0 | 0° | 0 | ||
|
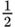
| 30° |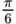
| ||
|
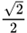
| 45° |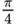 
| ||
|
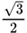
| 60° |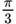 
| ||
| 1 | 90° |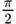 
| ||
Примечание: помни, что: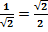 
Формулы исключения:
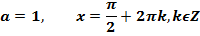
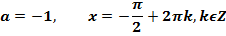
Уравнение вида cos x = a
Имеет решение только, если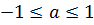 
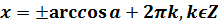
Значения арккосинусов берем из таблицы
(если значение нетабличное, но удовлетворяет условию существования решения, записываем просто: arccos (правая часть уравнения)):
| a | arccos a | |||
| град. | рад. | |||
| – 1 | 180° | π | ||
– 
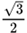
| 150° |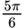 
| ||
– 
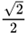
| 135° |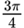 
| ||
– 
| 120° | 
| ||
| 0 | 90° | 
| ||
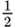
| 60° |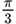 
| ||
| 45° |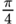 
| ||
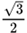
| 30° |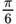 
| ||
| 1 | 0° | 0 | ||
Примечание: помни, что: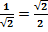
Формулы исключения:
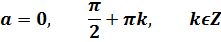
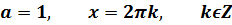
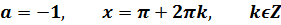
Уравнение вида tg x = a
Имеет решение при любом значении a
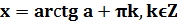
Значения арктангенсов берем из таблицы (если значение нетабличное, записываем просто: arctg (правая часть уравнения)):
| a | arctg a | |||
| град. | рад. | |||
| – ∞ | – 90° | –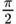 
| ||
– 
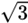
| – 60° | –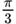 
| ||
| – 1 | – 45° | –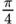 
| ||
– 
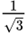
| – 30° | –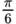 
| ||
| 0 | 0° | 0 | ||
|
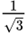
| 30° |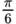
| ||
| 1 | 45° |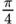
| ||
|
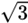
| 60° |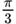
| ||
| + ∞ | 90° |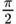
| ||
Примечание: помни, что: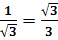 
Уравнение вида ctg x = a
Имеет решение при любом значении a
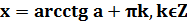
Значения арктангенсов берем из таблицы (если значение нетабличное, записываем просто: arcctg (правая часть уравнения)):
| a | arcctg a | |||
| град. | рад. | |||
| – ∞ | 180° | π | ||
| –
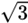
| 150° |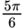 
| ||
| – 1 | 135° |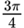 
| ||
| –
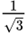
| 120° |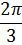 
| ||
| 0 | 90° |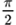 
| ||
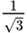
| 60° |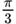
| ||
| 1 | 45° |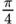
| ||
|
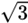
| 30° |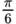
| ||
| + ∞ | 0° | 0 | ||
Примечание: помни, что: 
Основные логарифмические формулы
loga 1 = 0
loga a = 1
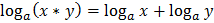
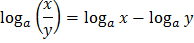
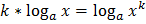
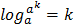
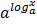=x
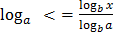- формула перехода к новому основанию
– натуральный логарифм, логарифм по основанию е (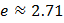 
)
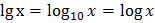– десятичный логарифм, логарифм по основанию 10
Производные. Основные формулы
Производная от константы
c ′ = 0, где c = const
Производная степенной функции
(xn )′ = n · xn – 1
(x )′ =1
Дата добавления: 2018-10-26; просмотров: 306; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!