Формалистское и интуитивистское обоснование математики
Перед тем как обратиться к острому методологическому противостоянию «формализма» и «интуиционизма», посмотрим на его исторические предпосылки. Это имеет для нас не только историческое, но и систематическое значение. Кажется, многих недоразумений в борьбе противостоящих направлений можно было бы избежать, если бы представители обоих лагерей яснее сознавали, что обсуждаемая ими проблема имеет долгую предысторию в логике и в философии. Уже у Аристотеля мы находим замечание, указывающее на то, что сущность геометрических дефиниций следует искать не в простом прояснении понятий, но в объяснении, включающем в себя теорему существования и доказательство существования. Значение слова «треугольник» предполагается геометром, но он доказывает, что имеется треугольник87. Понятие геометрической «конструкции» в античной философской и математической теории также было теснейшим образом связано с проблемой доказательства существования88. «Возрождение» математического способа мышления, происходившее в XVI— XVII вв., начинается именно с этого пункта. Спиноза и Гоббс, Чирнгауз и Лейбниц работали в одном и том же направлении: для всех них проблема генетической или, как они ее называли, «каузальной» дефиниции обретала далеко выходящее за пределы математики систематически-философское значение89. Методологические проницательность и мастерство Лейбница позволили ему обобщить все эти попытки и указать их место в целостном строении логики. Борьба между «номинализмом» и «реализмом», проходившая сквозь всю средневековую логику, принимает теперь новую форму: она как бы освобождается от пустых спекуляций и переходит в область конкретной работы точной науки. Гоббс пытался показать, что истинность и всеобщность основных математических понятий представляет собой лишь словесные истинность и всеобщность. Они имеют свое основание, по Гоббсу, не в вещи, но в слове; они покоятся на согласии относительно языковых знаков. На это Лейбниц возражает, что сам знак, если он имеет значение, должен быть связан с определенными объективными условиями. Математические символы и характеристики не могут образовываться произвольно и соединяться по одному лишь субъективному хотению, но они подчиняются определенным нормам связности, предписываемым им необходимостью вещей. Эти «вещи», на которые они должны постоянно ориентироваться (и внутреннюю логику которых они должны выражать), не следует мыслить как эмпирические «вещи», но как наличие определенных отношений, подпадающих под чистые идеи. В них находят свое основание и свою внутреннюю меру все математические понятия и знаки. Соединение характеристик должно соответствовать объективным отношениям идей90. «Ars characteristica est ars ita formandi atque ordinandi characteres, ut referant cogitationes, seu ut eam
|
|
|
286
|
|
|
inter se habeant relationem, quam cogitationes inter se habeant. Expressio est aggregatum characterum rem quae exprimitur repraesentantium. Lex expressionum haec est: ut ex quarum rerum ideis componitur rei exprimendae idea, ex illarum rerum characteribus componatur rei expressio»91. Тем самым однозначно устанавливается связь математической «формулы» и положения вещей. Формула обладает сигнификативной функцией лишь в силу своей направленности на положение вещей; поэтому она должна улавливать все сущностные черты этого положения вещей, четко и точно их выражать.
Построение мира математических знаков, создание и соединение единичных «характеров» с самого начала подпадает у Лейбница под одно ограничивающее условие: требуется достоверно установить «возможность» комбинируемого нами предмета. Не всякая связь элементов мышления и соответствующих им знаков представляет собой возможный объект мышления. Ведь встречаются такие элементы, которые, при попытке синтетического их объединения, не определяют и не детерминируют друг друга в этом синтезе, но вместо этого снимают друг друга. Не каждая фактически проводимая комбинация знаков соответствует «в себе» возможной, логически определенной и обоснованной структуре. Такое «основание» (fundamentum in re) должно особым образом полагаться и доказываться для любого понятийного образования. Дефиниция не дана тем самым как готовая и завершенная, обозначающая свой предмет одним лишь указанием отличительного признака или суммы таких признаков. В подобном случае возникает опасность того, что эта сумма состоит из взаимно уничтожающих друг друга компонентов. Эта опасность особенно усиливается, когда мы имеем дело с бесконечным многообразием. Мы всегда можем столкнуться со случаем, когда вполне допустимые и надежные в области конечного способы образования понятий приводят нас к определениям, противоречащим структурному принципу многообразного. Например, мы всегда можем указать «самое большое» число в конечном ряду чисел, но при перенесении на бесконечное множество понятие «наибольшего» включает в себя противоречие. С аналогичной ситуацией мы имеем дело в случае таких понятийных образований, как «наименьшая дробь» или «наименьшая скорость».
|
|
|
Лейбниц не останавливается на отдельных примерах понятий с взаимоисключающими элементами, но он использует их для выведения общего следствия. Любое понятие, с чьей помощью мы хотим обозначить или определить математический объект только за счет наименования привходящего единичного свойства, оказывается ненадежным. Простое указание на характерные признаки еще не гарантирует того, что им нечто соответствует в области содержания мышления. Например, если мы определяем круг как такую кривую на плоскости, которая, при данной длине линии, включает в себя максимум поверхности, то остается открытым вопрос: «имеется» ли такая кривая (с учетом предпосылок нашей геометрии), а если она имеется, то выполняется ли поставленное условие только кривой такого рода? В первом случае не определяется вообще никакая геометрическая форма; во втором случае она не определяется совершенно и однозначно. От сомнений мы избавимся в этом случае, только указав на способ построения (modus generandi) окружности, строго
|
|
|
287
дедуктивно показывая, что этот способ с необходимостью включает в себя заданное вместе с ним искомое свойство. Только тогда дефиниция, ранее имевшая лишь номинальный характер, превращается в настоящую «реальную дефиницию», т. е. такую, при которой предмет строится из конститутивных элементов. Однако, по Лейбницу, в согласованности и внутренней последовательности этого построения мы удостоверяемся только благодаря тому, что каждому совершаемому шагу мышления соответствует аналогичная операция со знаками. Когда каждой простой «идее» отвечает простой знак и установлены некие общие правила соединения знаков, то тем самым мы получаем символический язык с присущими ему законами. Нарушение этих законов, происходящее при образовании «невозможных» предметных понятий, тогда неизбежно обнаруживается в самой знаковой форме, и мы способны различать и распознавать скрытое логическое противоречие по непосредственным чувственно воспринимаемым симптомам. Принадлежащее миру чистых понятий отношение улавливается в образах: мы словно принуждаем мысль выйти из ее внутренней мастерской и прямо явиться перед нами в ее переплетениях и сочетаниях92.
Эта теория математической дефиниции и математического предмета устанавливает четко определенное и строгое отношение между «чувственностью» и «разумом». Две эти области ясно различаются: они не смешиваются и нигде друг в друга не переходят. Никакое математическое содержание как таковое не проистекает из чувственности, ибо последняя лишена характерного признака, конститутивного принципа математического. Чтобы считаться математическим, это содержание должно улавливаться отчетливо, т. е. оно должно строиться из простых базисных элементов познания — точно так же, как любое число можно однозначно представить как произведение простых чисел. Чувственные переживания не поддаются такому полному анализу: мы вынуждены останавливаться на целостностях, которые далее не разлагаются на конститутивные моменты и определяющие их «основания», но улавливаются нами лишь как «смутные». Из этого разделения «отчетливого» и «смутного» познания прямо следует то, что для Лейбница ни один истинно математический объект не может иметь своим основанием чувственность. Это относится не только к числу, но не менее строго утверждается относительно геометрической протяженности. Она также никоим образом не есть данность восприятия, но является идеей чистого рассудка (une ideve de l'entendement pur)93. Но даже после объявления рассудка истоком всей математики Лейбниц убежден в том, что человеческое познание укореняется и становится на твердую почву в области «интеллигибельных» математических предметов, когда оно прибегает к помощи чувственных знаков. В основе любого человеческого познания лежат первоначальные интуиции разума, но познание овладевает ими и сохраняет их только за счет того, что они улавливаются в образах, в символах. Интуитивное всегда остается первым «по сущности»,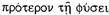 
; символическое незаменимо как «первое для нас», как 
. Наш конечный рассудок нуждается в образах, и он непременно заблудился бы в лабиринте мысли, если бы не та нить Ариадны, которую дает ему универсальная характеристика. В чисто логическом порядке, в порядке «предметов», ин-
288
туитивное всегда образует истинный фундамент; но мы способны достичь его только посредством чувственности, проходя через промежуточный слой символического94.
Это простое и ясное отношение между математическим «разумом» и «чувственностью» усложняется вместе с переходом от Лейбница к Канту. В одном пункте кантовское учение о математике, впрочем, является прямым продолжением лейбницевского: Кант также делает конструируемость основных математических понятий необходимым условием их истинности и значимости. Этот взгляд становится у Канта центральным для учения о математическом методе еще в работах докритического периода. Ни одно математическое понятие не получить с помощью простой «абстракции» от данного; оно всегда включает в себя свободный акт соединения, акт «синтеза». Доказательство «возможности» такого синтеза является и необходимым, и достаточным условием истинности математического предмета. «Конус может вообще обозначать что угодно, но в математике он возникает из произвольного представления о прямоугольном треугольнике, вращающемся вокруг одной из своих сторон. Определение здесь, как и во всех других случаях, возникает явно посредством синтеза»95. В конечном счете всякая математическая демонстрация опирается на конструкцию. Философское познание есть разумное познание в понятиях; математическое познание заключается в конструировании понятий. Однако, полагая момент конструирования важнейшим признаком математического образования понятий, Кант осуществляет иное, чем Лейбниц, расчленение того познания, которое обосновывается этим конструированием. Разделительная линия проходит в другой части системы в целом. Для Лейбница речь шла о том, что чисто разумное познание четко отличается от чувственного познания по своему оправданию, хотя оба они тесно связаны друг с другом с помощью «универсальной характеристики» в их применении. Математическое и логическое мышление находятся по одну сторону: они принадлежат миру чистого рассудка, intellectus ipse. Они вместе противостоят миру восприятия, простых «истин факта», но это отличие нигде не становится противоречием, истинным конфликтом между ними. Основной метафизический принцип философии Лейбница есть принцип «предустановленной гармонии», распространяющийся также на отношение разума и опыта. Истину чистого разума не получить из опыта, из рассмотрения единичных чувственных примеров, но каждая истина такого рода без всяких ограничений значима для опыта. Между логикой и математикой, с одной стороны, и эмпирико-физическим познанием — с другой, никогда не возникает раскол — в системе Лейбница нет места проблеме применимости математики.
Но именно эта проблема заостряется Кантом, и именно она придает окончательную форму его «критическому» учению. Он отбрасывает догматическую трактовку «предустановленной гармонии» и ставит вопрос об условиях возможности согласованности априорных понятий и эмпирических фактов. Ответ на этот вопрос гласит, что и эмпирический предмет, будучи предметом, не просто дан, но включает в себя момент математической конструкции. Эмпирическая предметность реализуется только на основании эмпирического порядка, а он возможен лишь благодаря чистому чувственному созерцанию пространства и времени. Это понятие
289
чистого созерцания отходит как от «сенсуализации» познания Локком, так и от его «интеллектуализации» Лейбницем. Математическое не обладает теперь особым логическим достоинством; его значение, его quid juris, полностью выявляется его участием в построении эмпирического познания. Без этой постоянной связи, без учета такого участия учение о «чистом пространстве» и «чистом времени» есть лишь «увлеченность призраками». Кант заходит столь далеко, что заявляет: «Все математические понятия сами по себе не знания, если только не предполагать, что существуют вещи, которые могут представляться нам только сообразно с формой этого чистого чувственного созерцания»96. Истинность математических идей оказывается теснейшим образом связанной с их эмпирическим исполнением. Методика конструктивного построения тем самым отвоевывает себе новую область: она в известной степени входит в царство опытного познания. Однако это имеет одновременно и то следствие, что, в сравнении с теорией познания Лейбница, существенно увеличивается дистанция между логическим и математическим познанием. Не соотносясь с чистыми формами созерцания, пространством и временем, мышление становится совокупностью аналитических суждений, хотя и не содержащих в себе противоречий, но не имеющих права притязать на какую бы то ни было плодотворную роль в познании в целом.
Это показывает, что требование «конструируемости» обладает в кантовской системе двояким значением. С одной стороны, им утверждается тот же самый принцип, который мы уже обнаруживали работающим в лейбницевском учении о «генетической дефиниции»: все «данное» должно быть понято и выведено из «порождающего правила». С другой стороны, «дать дефиницию» понятия для Канта означает: непосредственно представить это понятие в созерцании, т. е. уловить его в пространственной или временной схеме. «Смысл» математических понятий связывается теперь с этой формой схематизации. Поэтому «чистая чувственность» занимает в целостном строении математики совсем иное место, чем у Лейбница. Из простого средства представления, каковым чувственность была у Лейбница, она превращается в самостоятельное основание познания: созерцание обретает фундирующую и легитимирующую ценность. Для Лейбница относимая к объективной связи идей область интуитивного познания отделялась от области символического познания, где мы имели дело не с самими идеями, но с представляющими их знаками. Интуиция для него не образует противостоящую логическому инстанцию, но она включает в себя логическое и математическое как свои особые формы. Напротив, для Канта граница проходит не между интуитивным и символическим мышлением, но между «дискурсивным» понятием и «чистым созерцанием», причем содержание математического находит свое основание только в последнем.
Если посмотреть на это методологическое расхождение с точки зрения современной математики, то следует сказать, что она пошла здесь по пути, проложенному Лейбницем, а не Кантом. Этому поспособствовало в первую очередь открытие неэвклидовой геометрии. Благодаря полученным таким образом новым проблемам математика все более делалась «гипотетико-дедуктивной системой», истинность которой заключалась исключительно в ее внутренней логической согласованности и последова-
290
тельности, а основанием ее не могли быть какие бы то ни было материальные суждения созерцания. Математика прибегает к созерцанию не с целью положительного доказательства или обоснования, но пользуется им лишь для конкретной репрезентации общих систем отношений, созданных чистым мышлением. Она показывает, что таких репрезентаций имеется бесконечно много, что определенная система «аксиом» реализуется не в какой-то единичной области данных созерцания, но может реализовываться самым различным образом. Ею не оспаривается разнообразие репрезентаций, но это разнообразие перестало быть математически значимым фактом. С математической точки зрения, все многообразие областей созерцания означает лишь один объект и одну форму: все они «изоморфны» друг другу, поскольку для всех них равно значимо отношение R', R'' и т.д., причем, согласно новому воззрению, ставшему общепринятым в XIX-XX вв., именно значимость чистых отношений конституирует математическую форму как таковую97. Уже один из основоположников современной «символической логики», Джордж Буль, определял понятие «формальной науки» именно в том смысле, который получил полное подтверждение в развитии «абстрактной» математики. Он отмечал, что значимость процесса анализа зависит не от интерпретации используемых символов, а от законов их соединения.
Тем удивительнее, на первый взгляд, могло показаться, что все трудности, заключающиеся в понятии и в проблеме «созерцания», заявили о себе в последние десятилетия в самой математике и обрели в ней все возрастающий объем. Борьба в ней сегодня приняла форму кризиса, а отношение математики и логики вновь стало неоднозначным и спорным. По одну сторону стоят те, кто не только обосновывает чистую математику логикой, но желает целиком свести первую ко второй и принципиально оспаривает всякую возможность их разграничения98. По другую сторону стоят те, кто энергично подчеркивает собственные права и смысл математического: не только «предмет» математики становится у них независимым от логики, но они решаются напасть даже на фундаментальные принципы «классической» логики, вроде «закона исключенного третьего». С этой точки зрения логика никак не является фундаментом всякого мышления, поскольку имеются совершенно автономные и не выводимые из логики акты мышления. Логика не закладывает подлинные основания истинности, но она получает все то, что обладает значением и истиной от другой инстанции — от достоверности изначальной математической интуиции.
Для Брауэра, представляющего это воззрение в самой резкой форме, в начале всякого мышления лежит числовое мышление: элементарные правила логики были абстрагированы из теории числа, из арифметики. Поначалу как математика, так и логика имели дело с конечными множествами. Они выдвигали правила для таких множеств и допускали только те процессы, которые можно было привести к определенному «завершению», к окончательному решению. Но стоило преодолеть эти ограничения и продвинуться к концепциям, включающим в себя понятие бесконечного, как мы столкнулись с совершенно новой проблемой, к которой не применимы имеющиеся инструменты. По мнению Брауэра, современный анализ безуспешно пытался совладать с этой проблемой: чем даль-.
291
ше он шел, тем больше запутывался в парадоксах и противоречиях. Спасением от этих противоречий будет не выработка новых инструментов, но критическое ограничение возможных объектов мышления. Теория множеств приобретет непротиворечивую форму только после того, как она оставит попытки искусственного выхода мышления за его собственные границы, но сознательно ограничит себя конечными процессами". Современная математика сталкивается здесь с подлинной методологической дилеммой. Каким бы ни было ее решение, от чего-то математике придется отказываться. Если она желает сохранить за собой прежнюю славу «очевидности», то это, кажется, может быть достигнуто только за счет возврата к первоистоку этой очевидности, к фундаментальной интуиции целого числа. Но в то же самое время этот возврат возможен лишь за счет значительных интеллектуальных жертв: математике грозит утрата обширных и плодоносных областей, которые шаг за шагом отвоевывались классическим анализом. В рамках самой математики окончательного завершения этой борьбы пока не видно100. Каким бы оно ни было, с точки зрения чистой теории познания, уже сам факт этой борьбы делает явной важную и плодотворную проблему; демонстрируемое подвижное равновесие отчетливо показывает теоретику познания природу различных интеллектуальных сил, участвовавших в построении современной математики и становлении ее нынешней формы.
Дата добавления: 2018-09-20; просмотров: 247; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!