Тема. Средние величины в статистическом анализе
Как правило, многие признаки единиц статистических совокупностей различны по своему значению, например, заработная плата рабочих одной профессии какого-либо предприятия не одинакова за один и тот же период времени, различны урожайность сельскохозяйственных культур в хозяйствах района и цены на рынке на одинаковую продукцию и т.д. Поэтому, чтобы определить значение признака, характерное для всей изучаемой совокупности единиц, прибегают к расчету средних величин.
Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности.
Вычисление среднего — один из распространенных приемов обобщения; средний показатель отражает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц. В каждом явлении и его развитии имеет место сочетание случайности и необходимости. При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются, поэтому можно абстрагироваться от несущественных особенностей явления, от количественных значений признака в каждом конкретном случае. В способности абстрагироваться от случайности отдельных значений, колебаний и заключена научная ценность средних как обобщающих характеристик совокупностей.
|
|
|
Там, где возникает потребность обобщения, расчет таких характеристик приводит к замене множества различных индивидуальных значений признака средним показателем, характеризующим всю совокупность явлений, что позволяет выявить закономерности, присущие массовым общественным явлениям, незаметные в единичных явлениях.
Средняя отражает характерный, типичный, реальный уровень изучаемых явлений, характеризует эти уровни и их изменения во времени и в пространстве.
Средняя — это сводная характеристика закономерностей процесса в тех условиях, в которых он протекает.
Однако для того, чтобы средний показатель был действительно типизирующим, он должен определяться не для любых совокупностей, а только для совокупностей, состоящих из качественно однородных единиц. Это является основным условием научно обоснованного использования средних.
Средние, полученные для неоднородных совокупностей, будут искажать характер изучаемого общественного явления, фальсифицировать его, или будут бессмысленными. Так, если рассчитать средний уровень доходов служащих какого-либо района, то получится фиктивный средний показатель, поскольку для его исчисления использована неоднородная совокупность, включающая в себя служащих предприятий различных типов (государственных, совместных, арендных, акционерных), а также органов государственного управления, сферы науки, культуры, образования и т.п. В таких случаях метод средних используется в сочетании с методом группировок, позволяющим выделить однородные группы, по которым и исчисляются типические групповые средние.
|
|
|
Групповые средние позволяют избежать "огульных" средних, обеспечивают сравнение уровней отдельных групп с общим уровнем по совокупности, выявление имеющихся различий и т.д.
Однако нельзя сводить роль средних только к характеристике типических значений признаков в однородных по данному признаку совокупностях. На практике современная статистика использует так называемые системные средние, обобщающие неоднородные явления (характеристики государства, единой народно-хозяйственной системы: например, средний национальный доход на душу населения, средняя урожайность зерновых по всей стране, средний реальный доход на душу населения, среднее потребление продуктов питания на душу населения, производительность общественного труда).
|
|
|
В современных условиях развития рыночных отношений в экономике средние служат инструментом изучения объективных закономерностей социально-экономических явлений. Однако в экономическом анализе нельзя ограничиваться лишь средними показателями, так как за общими благоприятными средними могут скрываться и крупные серьезные недостатки в деятельности отдельных хозяйствующих субъектов, и ростки нового, прогрессивного. Так, например, распределение населения по доходу позволяет выявлять формирование новых социальных групп. Поэтому наряду со средними статистическими данными необходимо учитывать особенности отдельных единиц совокупности.
Средняя должна исчисляться для совокупности, состоящей из достаточно большого числа единиц, так как в этом случае согласно закону больших чисел взаимопогашаются случайные, индивидуальные различия между единицами, и они не оказывают существенного влияния на среднее значение, что способствует проявлению основного, существенного, присущего всей массе. Если основываться на средней из небольшой группы данных, то можно сделать неправильные выводы, поскольку такой средний показатель будет отражать значительное влияние индивидуальных особенностей, т.е. случайных моментов, не характерных для изучаемой совокупности в целом.
|
|
|
Каждая средняя характеризует изучаемую совокупность по какому-либо одному признаку, но для характеристики любой совокупности, описания ее типических черт и качественных особенностей нужна система средних показателей. Поэтому в практике отечественной статистики для изучения социально-экономических явлений, как правило, исчисляется система средних показателей. Так, например, показатели средней заработной платы оцениваются совместно с показателями средней выработки, фондовооруженности и энерговооруженности труда, степенью механизации и автоматизации работ и др.
Средняя должна вычисляться с учетом экономического содержания исследуемого показателя. Поэтому для конкретного показателя, используемого в социально-экономическом анализе, можно исчислить только одно истинное значение средней на базе научного способа расчета.
Виды средних и способы их вычисления
Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. В каждом конкретном случае применяется одна из средних величин: арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т.д.
Средняя арифметическая
Наиболее распространенным видом средних является средняя арифметическая. Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Для общественных явлений характерна аддитивность (суммарность) объемов варьирующего признака, этим определяется область применения средней арифметической и объясняется ее распространенность как обобщающего показателя. Так, например, общий фонд заработной платы — это сумма заработных плат всех работников, валовой сбор урожая — сумма произведенной продукции со всей посевной площади.
Чтобы исчислить среднюю арифметическую, нужно сумму всех значений признаков разделить на их число.
Средняя арифметическая применяется в форме простой средней и взвешенной средней. Исходной, определяющей формой, служит простая средняя.
X Средняя арифметическая простая равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений (она применяется в тех случаях, когда имеются несгруппированные индивидуальные значения признака):
,
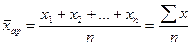где х1, x2, ..., хn - индивидуальные значения варьирующего признака (варианты);
п - число единиц совокупности.
Средняя из вариантов, которые повторяются различное число раз, или, как говорят, имеют различный вес, называется взвешенной. В качестве весов выступают численности единиц в разных группах совокупности (в группу объединяют одинаковые варианты).
Х Средняя арифметическая взвешенная — средняя сгруппированных величин х1, x2, ..., хn — вычисляется по формуле:
,
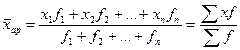где 
- веса (частоты повторения одинаковых признаков);
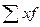- сумма произведений величины признаков на их частоты;
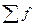- общая численность единиц совокупности.
Например, имеются данные о размере взносов учредителей
Таблица 1
| Размер взноса каждого учредителя, тыс. руб. х | Число учредителей, чел. f | хf |
| 60 80 90 100 | 3 4 3 5 | 180 320 270 500 |
| Итого: | 15 | 1270 |
По формуле вычислим среднюю арифметическую взвешенную:
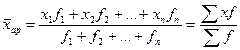
ХАР = (180 + 320 + 270 + 500) / 15 = 1270 / 15 = 84,7 тыс. руб.
Если значения признака заданы в виде интервальных рядов (“от - до”), то при расчете средней арифметической величины в качестве значений признаков принимают середины этих интервалов, в результате чего получается дискретный ряд.
Например, рассмотрим следующий пример:
Таблица 2
| Исходные данные | Расчетные значения | ||
| Группы работников по оплате труда, руб. | Число работников, чел. f | Середина интервала, руб. х | хf |
| До 1000 1000 - 1200 1200 - 1400 1400 - 1600 1600 - 1800 1800 и более | 5 15 20 30 16 14 | 900 1100 1300 1500 1700 1900 | 4 500 16500 26000 45000 27200 26600 |
| Итого | 100 | 145 800 | |
Первый столбец является интервальным рядом, от него перейдем к дискретному путем замены интервальных значений их средними значениями (простая средняя между верхней и нижней границами каждого интервала). При этом величины открытых интервалов (первый и последний) условно приравниваются к интервалам, примыкающим к ним.
После того как найдены середины интервалов, вычисления делают так же - варианты умножают на частоты (веса) и сумму произведений делят на сумму частот (весов), руб.:
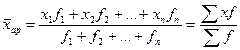
ХАР = 145 800 / 100 = 1458.
Итак средний уровень оплаты труда работников составляет 1458 руб. в месяц.
Средняя гармоническая
При расчете средних показателей помимо средней арифметической могут использоваться и другие виды средних. Однако любая средняя величина должна вычисляться так, чтобы при замене ею каждого варианта осредняемого признака не изменялся итоговый, обобщающий, или, как его принято называть, определяющий показатель, который связан с осредняемым показателем (например, при замене фактических скоростей на отдельных отрезках пути их средней скоростью не должно измениться общее расстояние, пройденное транспортным средством за одно и то же время; при замене фактических заработных плат отдельных работников предприятия средней заработной платой не должен измениться фонд заработной платы). Следовательно, в каждом конкретном случае в зависимости от характера имеющихся данных существует только одно истинное среднее значение показателя, адекватное свойствам и сущности изучаемого социально-экономического явления.
Вид средней определяется характером взаимосвязи определяющего показателя с осредняемым.
Средняя арифметическая, как было показано выше, применяется в тех случаях, когда известны варианты варьирующего признака х и их частоты f.
Когда статистическая информация не содержит частот f по отдельным вариантам х совокупности, а представлена как их произведение хf, применяется формула средней гармонической взвешенной. Чтобы исчислить среднюю, обозначим xf = w, откуда f = w/x. Теперь преобразуем формулу средней арифметической таким образом, чтобы по имеющимся данным х и w можно было исчислить среднюю. В формулу средней арифметической взвешенной (5.4) вместо xf подставим w, вместо f - отношение w/x и получим формулу средней гармонической взвешенной:
,
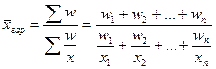Из формулы видно, что средняя гармоническая - средняя взвешенная из варьирующих обратных значений признака. Она является преобразованной формой арифметической средней и тождественна ей. Вместо гармонической всегда можно рассчитать среднюю арифметическую, но для этого сначала нужно определить веса отдельных значений признака, скрытые в весах средней гармонической.
Таким образом, средняя гармоническая применяется тогда, когда неизвестны действительные веса f, а известно w = хf, т.е. в тех случаях, когда средняя предназначается для расчета сумм слагаемых, обратно пропорциональных величине данного признака, когда суммированию подлежат не сами варианты, а обратные им величины.
Исчисление средней гармонической взвешенной по формуле освобождает от необходимости предварительного расчета весов, поскольку эта операция заложена в саму формулу.
Например, по данным таблицы определим среднюю цену 1 кг яблок:
Таблица 3
| Номер магазина | Исходные данные | |
| Цена яблок, руб./кг, | Выручка от реализ, руб., | |
| 1 2 3 | 17 20 24 | 3060 2800 1920 |
| 7780 | ||
Среднюю цену 1 кг яблок по трем магазинам исчислим по формуле средней гармонической взвешенной:
ХГАР = (3060+2800+1920) / (3060/17+2800/20+1920/24) = 7780 / 400 = 19,45
Средняя геометрическая
Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню
каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста.
Средняя геометрическая исчисляется извлечением корня степени и из произведений отдельных значений — вариантов признака х:
,
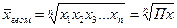где n — число вариантов; П — знак произведения.
Наиболее широкое применение средняя геометрическая получила для определения средних темпов изменения в рядах динамики, а также в рядах распределения.
Использование средней геометрической показано в гл. 7.
Средняя квадратическая и средняя кубическая
В ряде случаев в экономической практике возникает потребность расчета среднего размера признака, выраженного в квадратных или кубических единицах измерения. Тогда применяется средняя квадратическая и средняя кубическая. Формулы для расчета средней квадратической:
X средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:
,
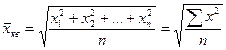X средняя квадратическая взвешенная
,
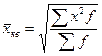где f — веса.
Формулы для расчета средней кубической аналогичны:
X средняя кубическая простая
,
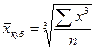X средняя кубическая взвешенная
,
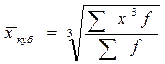Средние квадратическая и кубическая имеют ограниченное применение в практике статистики. Широко пользуется статистика средней квадратической, но не из самих вариантов х, и из их отклонений от средней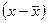 
при расчете показателей вариации).
Структурные средние
Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.
Х Мода m 0 — значение случайной величины, встречающееся с наибольшей вероятностью в дискретном вариационном ряду — вариант, имеющий наибольшую частоту.
Например, в таблице 4
Таблица 4
| Размер взноса каждого учредителя, тыс. руб. | Число учредителей, чел. |
| 60 80 90 100 | 3 4 3 5 |
| Итого: | 15 |
наибольшей частотой является число 5, этой частоте соответствует модальное значение признака, т.е. размер взноса учредителей. Мода свидетельствует, что в данном примере больше всего учредителей которые внесли по 100 тыс. руб.
В интервальных рядах распределения с равными интервалами мода вычисляется по формуле:
,
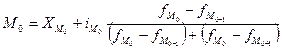где xm0 — нижняя граница модального интервала; iM0 — модальный интервал; fM0 , fM0-1 , fM0+1 - частоты в модальном, предыдущем и следующем за модальным интервалах (соответственно).
Пример. Модальный интервал определяется по наибольшей частоте.
Таблица 5
| Группы предприятий по стоимости ОПФ, млн. руб. | Число предприятий |
| 14 -16 16 -18 18 -20 20 -22 22 - 24 | 2 6 10 4 3 |
| Итого: | 25 |
По данным таблицы рассчитаем моду, млн. руб.:
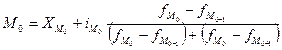
Мо= 18 + 2 х [ (10-6) / (10-6+10-4)] = 18,8
Итак модальным значением стоимости ОПФ предприятий региона является стоимость, равная 18,8 млн. руб.
X Медиана М e - это вариант, который находится в середине вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части — со значениями признака меньше медианы и со значениями признака больше медианы. Чтобы найти медиану, необходимо отыскать значение признака, которое находится в середине упорядоченного ряда. В ранжированных рядах несгруппированных данных нахождение медианы сводится к отысканию порядкового номера медианы.
В случае четного объема ряда медиана равна средней из двух вариантов, находящихся в середине ряда.
В интервальных рядах распределения медианное значение (поскольку оно делит всю совокупность на две равные по численности части) оказывается в каком-то из интервалов признака х. Этот интервал характерен тем, что его кумулятивная частота (накопленная сумма частот) равна или превышает полусумму всех частот ряда. Значение медианы вычисляется линейной интерполяцией по формуле:
,
где XMe — нижняя граница медианного интервала; iMe — медианный интервал; åf/2 - половина от общего числа наблюдений; SМe - сумма наблюдений, накопленная до начала медианного интервала; fMe - число наблюдений в медианном интервале.
Пример. Рассчитаем медиану по данным таблицы 6
Таблица 6
| Группы предприятий по стоимости ОПФ, млн. руб. | Число предприятий |
| 14 -16 16 -18 18 -20 20 -22 22 - 24 | 2 6 10 4 3 |
| Итого: | 25 |
Прежде всего найдем медианный интервал, он должен превышать половину суммы всех частот (25:2=12,5), возьмем первый интервал 14-16, его частота равна 2, 2 меньше 12,5 (неподходит); возьмем второй интервал 16-18, его накопленная частота равна 2+6=8, 8 меньше 12,5, третий интервал 18-20, его накопленная частота 2+6+10 = 18, 18 превышает 12,5. Нижняя граница интервала 18 млн. руб., его частота 10, частота накопленная до него, равна 8.
Подставив данные в формулу, найдем значение медиан, млн. руб.
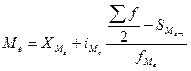
Ме = 18 + 2 х [(25/2 - 8) / 10] = 18,9
Полученный результат говорит о том, что из 25 предприятий региона 12 предприятий имеют стоимость ОПФ менее 18 млн. руб., а 12 предприятий - более.
Тема: Вариационный анализ
Вариация — это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.
Вариация возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Таким образом, величина каждого варианта объективна.
Исследование вариации в статистике имеет большое значение, помогает познать сущность изучаемого явления. Особенно актуально оно в период формирования многоукладной экономики. Измерение вариации, выяснение ее причины, выявление влияния отдельных факторов дает важную информацию для принятия научно обоснованных управленческих решений.
Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывает строения совокупности, которое весьма существенно для ее познания. Средняя не показывает, как располагаются около нее варианты осредняемого признака, сосредоточены ли они вблизи средней или значительно отклоняются от нее. Средняя величина признака в двух совокупностях может быть одинаковой, но в одном случае все индивидуальные значения отличаются от нее мало, а в другом — эти отличия велики, т.е. в одном случае вариация признака мала, а в другом — велика, это имеет весьма важное значение для характеристики надежности средней величины.
Чем больше варианты отдельных единиц совокупности различаются между собой, тем больше они отличаются от своей средней, и наоборот, — чем меньше варианты отличаются друг от друга, тем меньше они отличаются от средней, которая в таком случае будет более реально представлять всю совокупность. Вот почему ограничиваться вычислением одной средней в ряде случаев нельзя. Нужны и другие показатели, характеризующие отклонения отдельных значений от общей средней.
Поэтому возникает необходимость измерять вариацию признака в совокупностях. Для этой цели в статистике применяют ряд обобщающих показателей.
X К показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, коэффициент вариации.
X Самым элементарным показателем вариации признака является размах вариации R, представляющий собой разность между максимальным и минимальным значениями признака:
R= хmax - хmin
Однако размах вариации показывает лишь крайние отклонения признака и не отражает отклонений всех вариантов в ряду. При изучении вариации нельзя ограничиваться только определением ее размаха. Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и даёт обобщённую характеристику. Простейший показатель такого типа — среднее линейное отклонение.
X Среднее линейное отклонение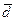 
представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической (при этом всегда предполагают, что среднюю вычитают из варианта: 
.
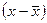Среднее линейное отклонение:
• для несгруппированных данных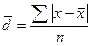 
,
где п - число членов ряда;
• для сгруппированных данных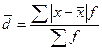 
,
где åf — сумма частот вариационного ряда.
X Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных):
• простая дисперсия для несгруппированных данных
;
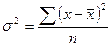• взвешенная дисперсия для вариационного ряда
,
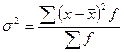Формула применяется при наличии у вариантов своих весов (или частот вариационного ряда).
Формулу для расчета дисперсии можно преобразовать,
учитывая, что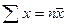 
:
,
т.е. дисперсия равна разности средней из квадратов вариантов и квадрата их средней.
Используя второе свойство дисперсии, разделив все варианты на величину интервала, получим следующую формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:
,
где s - дисперсия, исчисленная по способу моментов;
i - величина интервала;
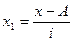- новые (преобразованные) значения вариантов
(А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой);
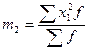- момент второго порядка;
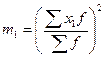- квадрат момента первого порядка.
Дисперсия имеет большое значение в экономическом анализе. В математической статистике важную роль для характеристики качества статистических оценок играет их дисперсия. Ниже, в частности, будет показано разложение дисперсии на соответствующие элементы, позволяющие оценить влияние различных факторов, обуславливающих вариацию признака; использование дисперсии для построения показателей тесноты корреляционной связи при оценке результатов выборочных наблюдений.
X Среднее квадратическое отклонение s равно корню квадратному из дисперсии:
· для несгруппированных данных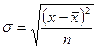 
,
• для вариационного ряда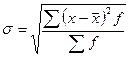 
,
Среднее квадратическое отклонение - это обобщающая характеристика размеров вариации признака в совокупности; оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения; является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, поэтому экономически хорошо интерпретируется.
Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:
,
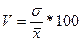Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33 %.
Пример. Рассмотрим расчет различными способами показателей вариации на примере данных таблицы 7
Таблица 7
| Группы п/тий по объему т/о, млн. руб | Число предприятий |
| f | |
| 170-190 | 10 |
| 190-210 | 20 |
| 210-230 | 50 |
| 230-250 | 20 |
| Итого | 100 |
Рассчитаем дисперсию по трем, приведенным выше формулам.
1. 
2. 
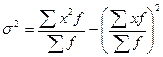
3. 
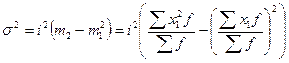
Исчислим средний объем товарооборота, млн. руб.:
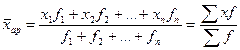
ХАР = 21 600 / 100 = 216
Далее строим вспомогательную таблицу и делаем расчеты
| Группы п/тий по объему т/о, млн. руб | Число предпри- ятий | Середи-ны интерва-лов |
Расчетные значения | |||||||
| f | x | f x | (x-x) | (x-x)2 | (x-x)2f | x2 f | x1 | x1 f | x12f | |
| 170-190 | 10 | 180 | 1 800 | - 36 | 1 296 | 12 960 | 324 000 | - 2 | - 20 | 40 |
| 190-210 | 20 | 200 | 4 000 | - 16 | 256 | 5 120 | 800 000 | - 2 | - 20 | 20 |
| 210-230 | 50 | 220 | 11 000 | 4 | 16 | 800 | 2 420 000 | 0 | 0 | 0 |
| 230-250 | 20 | 240 | 4 800 | 24 | 576 | 11 520 | 1 152 000 | 1 | 20 | 20 |
| Итого | 100 | - | 21 600 | - | - | 30 400 | 4 696 000 | - | - 20 | 80 |
Взяв расчетные данные из таблицы, подставляем их в наши формулы (1,2,3)
1. = 30 400 / 100 = 304
2. 
= 4 696 000/100 – (216)2 = 304
3. 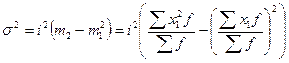= 202 х (80/100 – (-20/100)2) = 304
где А = 50 центральный вариант с наибольшей частотой
i = 20 - величина интервала данного ряда
Определим коэффициент вариации, %
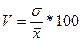= 17,44 / 216 х 100 = 8
Таким образом предприятия достаточно однородны по товарообороту, поскольку вариация признака составляет лишь 8%.
Теперь выполним расчет дисперсии по разным формулам:
Тема. Анализ рядов динамики
Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, т. е. их динамика. Эта задача решается при помощи анализа рядов динамики (или временных рядов).
Ряд динамики (или динамический ряд) представляет собой ряд расположенных в хронологической последовательности числовых значений статистического показателя, характеризующих изменение общественных явлений во времени.
В каждом ряду динамики имеются два основных элемента: время t и конкретное значение показателя (уровень ряда) у.
Уровни ряда — это показатели, числовые значения которых составляют динамический ряд. Время — это моменты или периоды, к которым относятся уровни.
Построение и анализ рядов динамики позволяют выявить и измерить закономерности развития общественных явлений во времени. Эти закономерности не проявляются четко на каждом конкретном уровне, а лишь в тенденции, в достаточно длительной динамике. На основную закономерность динамики накладываются другие, прежде всего случайные, иногда сезонные влияния. Выявление основной тенденции в изменении уровней, именуемой трендом, является одной из главных задач анализа рядов динамики.
По времени, отраженному в динамических рядах, они разделяются на моментные и интервальные.
Моментным рядом динамики называется такой ряд, уровни которого характеризуют состояние явления на определенные даты (моменты времени).
Поскольку в каждом последующем уровне содержится полностью или частично значение предыдущего уровня, суммировать уровни моментного ряда не следует, так как это приводит к повторному счету.
Интервальным (периодическим) рядом динамики называется такой ряд, уровни которого характеризуют размер явления за конкретный период времени (год, квартал, месяц).
Значения уровней интервального ряда в отличие от уровней моментного ряда не содержатся в предыдущих или последующих показателях, их можно просуммировать, что позволяет получать ряды динамики более укрупненных периодов. Например, суммирование уровней добычи нефти за каждый год по данным, приведенным выше, позволяет определить ее добычу за все восемь лет в целом и в среднем за год.
Интервальный ряд, где последовательные уровни могут суммироваться, можно представить как ряд с нарастающими итогами. При построении таких рядов производится последовательное суммирование смежных уровней. Этим достигается суммарное обобщение результата развития изучаемого явления с начала отчетного периода (месяца, квартала, года и т.д.).
Уровни в динамическом ряду, могут быть представлены абсолютными, средними или относительными величинами. Так, в рассмотренных рядах динамики уровни выражены абсолютными статистическими величинами. Средними величинами могут выражаться уровни, характеризующие динамику средней реальной заработной платы в промышленности, динамику урожайности зерновых культур (ц/га). Относительными величинами характеризуются, например, динамика доли городского и сельского населения (%) и уровня безработицы.
По расстоянию между уровнями ряды динамики подразделяются на ряды с равностоящими и неравностоящими уровнями по времени.
Если в рядах динамики прерывающиеся или неравномерные интервалы времени, то такие ряды являются неравностоящими.
Ряды динамики могут быть изображены графически. Графическое изображение позволяет наглядно представить развитие явления во времени и способствует проведению анализа уровней. Наиболее распространенным видом графического изображения для аналитических целей является линейная диаграмма, которая строится в прямоугольной системе координат: на оси абсцисс отмечается время, а на оси ординат — уровни ряда
Наряду с линейной диаграммой для графического изображения рядов динамики в целях популяризации широко используются столбиковая диаграмма, секторная диаграмма и другие виды диаграмм (фигурные, квадратные, полосовые и т.п.).
Правила построения рядов динамики
При построений динамических рядов необходимо соблюдать определенные правила: основным условием для получения правильных выводов при анализе рядов динамики и прогнозировании его уровней является сопоставимость уровней динамического ряда между собой.
Статистические данные должны быть сопоставимы по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета и др.
Сопоставимость по территории предполагает одни и те же границы территории. Вопрос о том, является ли это требование непременным условием сопоставимости уровней динамического ряда, может решаться по-разному, в зависимости от целей исследования. Так, при характеристике роста экономической мощи страны следует использовать данные в имеющихся границах территории, а при изучении темпов экономического развития следует брать данные по территории в одних и тех же границах. Объясняемся это тем, что изменение границ влияет на численность населения, объем продукции.
Сопоставимость по кругу охватываемых объектов означает сравнение совокупностей с равным числом элементов.
При этом нужно иметь в виду, что сопоставляемые показатели динамического ряда должны быть однородны по экономическому содержанию и границам объекта, который они характеризуют (однородность может быть обеспечена одинаковой полнотой охвата разных частей явления). Несопоставимость может возникнуть вследствие перехода ряда объектов (например, предприятий отрасли) из одного подчинения в другое. Однако сопоставимость не нарушается, если в отрасли в строй введены новые предприятия или отдельные предприятия прекратили работу.
Сопоставимость по времени регистрации для интервальных рядов обеспечивается равенством периодов времени, за которые приводятся данные. Нельзя, например, при изучении ритмичности работы предприятия сравнивать данные об удельном весе продукции по определенным декадам, так как число рабочих дней отдельных декад может оказаться существенно различным, что приводит к различиям в объеме выпуска продукции. Это относится и к рядам внутригодовой динамики с месячными, квартальными уровнями. Для приведения таких рядов динамики к сопоставимому виду исчисляют среднедневные показатели по декадам, месяцам, кварталам, которые затем сопоставляют, сравнивают.
Для моментных рядов динамики показатели следует приводить на одну и ту же дату.
Сопоставимость по ценам. При проведении к сопоставимому виду продукции, измеренной в стоимостных (ценностных) показателях, трудность заключается в том, что, во-первых, с течением времени происходит непрерывное изменение цен, а во-вторых, существует несколько видов цен. Для характеристики изменения объема продукции должно быть устранено (элиминировано) влияние изменения цен. Поэтому на практике количество продукции, произведенной в разные периоды, оценивают в ценах одного и того же базисного периода, которые называют неизменными, или сопоставимыми ценами.
Сопоставимость по методологии расчета. При определении уровней динамического ряда необходимо использовать единую методологию их расчета.
Нередко статистические данные выражаются в различных единицах измерения. С этим часто приходится сталкиваться при учете продукции в натуральном выражении. Например, данные о количестве произведённого молока могут быть выражены в литрах и килограммах. Для того чтобы обеспечить сравнимость такого ряда данных, необходимо выразить их в одних и тех же единицах измерения, т. е. или только в литрах, или только в килограммах (то же для валового сбора зерна — пуды и тонны).
Вполне очевидна несопоставимость денежных единиц разных стран, несопоставимость денежных единиц внутри одной страны за разные периоды времени (при изменении курса валюты).
Могут быть и другие причины несопоставимости уровней радов динамики.
Рассмотренные примеры показывают, что часто приходится иметь дело с такими несопоставимыми данными, которые могут быть приведены к сопоставимому виду дополнительными расчетами.
В ряде случаев несопоставимость может быть устранена путем обработки радов динамики приемом, который носит название смыкание рядов динамики. Этот прием позволяет преодолеть несопоставимость данных, возникающую вследствие изменения во времени круга охватываемых объектов или методологии расчета показателей, и получить единый сравнимый рад за весь период времени.
Таким образом, прежде чем анализировать динамические рады, следует убедиться в сопоставимости их уровней и, если сопоставимость отсутствует, добиться ее дополнительными расчетами, когда это возможно.
Показатели анализа ряда динамики
При изучении динамики общественных явлений возникает проблема описания интенсивности изменения и расчета средних показателей динамики.
Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней, к таким показателям относятся: абсолютный, прирост, темп роста, темп прироста, абсолютное значение одного процента прироста.
Система средних показателей включает средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста.
Показатели анализа динамики могут вычисляться на постоянной и переменных базах сравнения. При этом принято называть сравниваемый уровень отчетным, а уровень, с которым производится сравнение, — базисным.
Для расчета показателей анализа динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень, с которого начинается какой-то новый этап развития явления. Исчисляемые при этом показатели называются базисными.
Для расчета показателей анализа динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели анализа динамики называются цепными.
Важнейшим статистическим показателем анализа динамики является абсолютный прирост (сокращение), т.е. абсолютное изменение, характеризующее увеличение или уменьшение уровня ряда за определенный промежуток времени. Абсолютный прирост с переменной базой называют скоростью роста.
Абсолютный прирост (цепной): Dуц =уi - yi-1
Абсолютный прирост (базисный): Dyб = уi - y0
где уi — уровень сравниваемого периода;
yi-1 — уровень предшествующего периода;
y0 — уровень базисного периода
Для оценки интенсивности, т. е. относительного изменения уровня динамического ряда за какой-либо период времени исчисляют темпы роста (снижения).
Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному.
Показатель интенсивности изменения уровня ряда, выраженный в долях единицы, называется коэффициентом роста, а в процентах — темпом роста. Эти показатели интенсивности изменения отличаются только единицами измерения.
Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число.
Коэффициент роста (цепной)
Коэффициент роста (базисный)
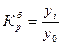
Темп роста (цепной):
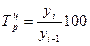
Темп роста (базисный):
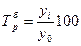
Относительную оценку скорости измерения уровня ряда в единицу времени дают показатели темпа прироста (сокращения).
Темп прироста (сокращения) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения, и вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения.
Темп прироста может быть положительным, отрицательным или равным нулю, выражается он в процентах и долях единицы (коэффициенты прироста).
Темп прироста (цепной):
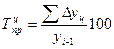
Темп прироста (базисный):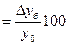 
Темп прироста (сокращения) можно получить и из темпа роста, выраженного в процентах, если из него вычесть 100%. Коэффициент прироста получается вычитанием единицы из коэффициента роста:
Тпр = Тр-100 Кпр = Кр-1
При анализе динамики развития следует также знать, какие абсолютные значения скрываются за темпами роста и прироста. Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что при снижении (замедлении) темпов прироста абсолютный прирост не всегда уменьшается, в отдельных случаях он может возрастать. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением (содержанием) одного процента прироста и рассчитывают как отношение абсолютного прироста к темпу прироста за тот же период времени, %:
,
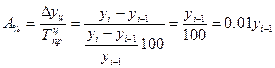Абсолютное значение одного процента прироста равно сотой части предыдущего (или базисного) уровня. Оно показывает, какое абсолютное значение скрывается за относительным показателем - одним процентом прироста.
В тех случаях, когда сравнение производится с отдалением периода времени, принятого за базу сравнения, рассчитывают так называемые пункты роста, которые представляют собой разность базисных темпов роста, %, двух смежных периодов.
В отличие от темпов прироста, которые нельзя ни суммировать, ни перемножать, пункты роста можно суммировать, в результате получаем темп прироста соответствующего периода по сравнению с базисным.
Для более глубокого понимания характера явления необходимо показатели динамики анализировать комплексно, совместно.
Для обобщающей характеристики динамики исследуемого явления определяют средние показатели: средние уровни ряда и средние показатели изменения уровней ряда.
Обобщающий показатель скорости изменения уровней во времени — средний абсолютный прирост (убыль), представляющий собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. По цепным данным об абсолютных приростах за ряд лет можно рассчитать средний абсолютный прирост как среднюю арифметическую простую:
,
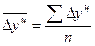где n - число цепных абсолютных приростов (Dуц) в изучаемом периоде.
Средний абсолютный прирост определим через накопленный (базисный) абсолютный прирост (Dуб). Для случая равных интервалов применим следующую формулу:
,
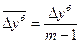где m - число уровней ряда динамики в изучаемом периоде, включая базисный.
Сводной обобщающей характеристикой интенсивности. изменения уровней ряда динамики служит средний темп роста (снижения), показывающий, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.
Средний темп роста (снижения) - обобщенная характеристика индивидуальных темпов роста ряда динамики. Поскольку средний темп роста представляет собой средний коэффициент роста, выраженный в процентах (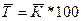 
), то для равностоящих рядов динамики расчеты по средней геометрической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по «цепному способу»):
,
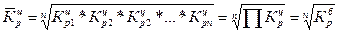где n - число цепных коэффициентов роста;
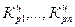- цепные коэффициенты роста; 
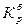- базисный коэффициент роста за весь период.
Если известны уровни динамического ряда, то расчет среднего коэффициента роста упрощается. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляется базисный коэффициент роста. Базисный коэффициент, как известно, получается непосредственно как частное от деления уровня последнего периода уn на уровень базисного периода у0.
Тогда формула для расчета среднего коэффициента роста для равностоящих рядов динамики (по «базисному способу»):
,
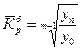где т — число уровней ряда динамики в изучаемом периоде, включая базисный.
Средние темпы прироста (сокращения) рассчитываются на основе средних темпов роста, вычитанием из последних 100 %. Соответственно при исчислении средних коэффициентов прироста из значений коэффициентов роста вычитается единица:
.
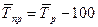
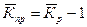где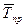 
— средний темп прироста, 
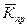— средний коэффициент прироста
Если уровни ряда динамики снижаются, то средний темп роста будет меньше 100%, а средний темп прироста - отрицательной величиной. Отрицательный темп прироста представляет собой средний темп сокращения и характеризует среднюю относительную скорость снижения уровня.
Пример. Используя данные таблицы, вычислим базисные и цепные: абсолютный прирост; темпы роста, темпы прироста, А%, пункты роста.
Основные показатели динамики товарооборота магазина в 2012 - 2016 гг.
Таблица 8
| Показатель | 2012 | 2013 | 2014 | 2015 | 2016 |
| Товарооборот, тыс.руб., у | 957 | 876 | 900 | 937 | 970 |
| 1. Абсолютный прирост, тыс.руб. yц = уi - yi-1 уб = уi - у0 2. Коэффициент роста КРЦ = уi / уi-1 КРБ= уi / у0 3. Темп роста, % ТРЦ = уi / уi-1 х 100 ТРБ= уi / у0 х 100 4. Темп прироста (сокращения), % ТПРЦ = ТРЦ - 100% ТПРБ = ТРБ -100% 5. Темп наращивания ТН = уЦ / у0 6. А%=уi-1 / 100 | - - - - - - - - - - | 876-957=-81 876-957=-81 876/957=0,915 876/957=0,915 0,915х100=91,5 0,915х100=91,5 91,5-100=-8,5 91,5-100=-8,5 -81/957=-0,085 9,57 | 900-876=24 900-957=-57 900/876=1,03 900/957=0,94 1,03х100=103 0,94х100=94 103-100=3 94-100=-6 24/957=0,025 8,76 | 937-900=37 937-957=-20 937/900=1,04 937/957=0,979 104 97,9 4 -2,1 0,039 9 | 33 13 1,04 1,01 104 101 4 1 0,034 9,37 |
Для обобщающей характеристики динамики исследуемого явления определяют средние показатели, которые рассчитываются по приведенным выше формулам.
Методы анализа основной тенденции развития в рядах динамики
Основной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления.
Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний.
Задача состоит в том, чтобы выявить общую тенденцию в изменении уровней ряда, освобожденную от действия различных случайных факторов.. На практике наиболее распространенными методами статистического изучения тренда являются: укрупнение интервалов, сглаживание скользящей средней, аналитическое выравнивание.
Метод укрупнения интервалов , основан на укрупнении периодов времени, к которым относятся уровни ряда динамики. Например, имеются данные о реализации радиоприемников в магазинах города, шт.
Таблица 9
| Период времени | Кол-во, проданных радиоприемников, шт. |
| Январь Февраль Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь | 3662 3096 2956 3805 3364 2946 3803 3812 3921 4442 3824 3976 |
По таким данным затруднительно сделать вывод об основной тенденции продажи радиоприемников. Решение задачи упрощается, если укрупнить интервалы, т.е. месячные уровни объединить в квартальные, из чего получим:
| Период времени | Кол-во, проданных радиоприемников, шт. |
| 1 квартал 2 квартал 3 квартал 4 квартал | 9714 10 115 11 536 12 242 |
После укрупнения интервалов основная тенденция роста продажи радиоприемников стала очевидной.
Выявление основной тенденции может осуществляться также методом скользящей средней.
Выявление основной тенденции может осуществляться также методом скользящей (подвижной) средней. Сущность его заключается в том, что исчисляется средний уровень из определенного числа, обычно нечетного (3, 5, 7 и т.д.), первых по счету уровней ряда, затем - из такого же числа уровней, но начиная со второго по счету, далее - начиная с третьего и т.д. Таким образом, средняя как бы «скользит» по ряду динамики, передвигаясь на один срок.
Сглаженный ряд урожайности по трехлетиям короче фактического на один член ряда в начале и в конце, по пятилетиям - на два члена в начале и конце ряда. Он меньше, чем фактический подвержен колебаниям из-за случайных причин, и четче, в виде некоторой плавной линии на графике, выражает основную тенденцию роста урожайности за изучаемый период, связанную с действием долговременно существующих причин и условий развития.
Недостатком сглаживания ряда является «укорачивание» сглаженного ряда по сравнению с фактическим, а, следовательно, потеря информации.
Пример. Расчет трехлетней скользящей средней о численности населения РФ за 2004-2013гг сделаем в таблице.
Таблица 10. Исходные данные и результаты расчета трехлетней скользящей средней, млн.чел.
| Год | Численность населения РФ, млн.чел | Трехлетняя скользящая средняя |
| 2004 | 144,3 | - |
| 2005 | 143,8 | (144,3+143,8+143,2) / 3=143,7 |
| 2006 | 143,2 | (143,8+143,2+142,8) / 3=143,3 |
| 2007 | 142,8 | 142,9 |
| 2008 | 142,8 | 142,8 |
| 2009 | 142,7 | 142,8 |
| 2010 | 142,8 | 142,8 |
| 2011 | 142,9 | 142,9 |
| 2012 | 143,0 | 143,1 |
| 2013 | 143,3 | - |
Дата добавления: 2018-09-20; просмотров: 3995; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!