Покажите, что НЛО оценка параметров линейной регрессионной модели является несмещенной.

НЛО является оценка

Имеем = ;

= поскольку действует предположение A1: .

Недостатки и достоинства максимальной парной сопряженности как меры измерения мультиколлинеарности.

. В качестве показателя мультиколлинеарности может выступать величина .Достоинства: максимальный коэффициент сопряженности не несет на себе эффекта масштаба. Существенный недостаток: она ориентирована только на парную коллинеарность. (три вектора могут быть коллинеарны, а попарно нет). Поэтому даже если 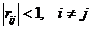возможна строгая (= 0) в 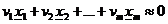мультиколлинеарность.

Оценивание параметров в модели регрессии при наличии линейных ограничений. Проверка общей линейной гипотезы.

Пусть модель имеет вид:

, где 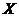- матрица ранга . Предположим, что мы хотим найти оценки параметра , минимизируя , при наличии линейных ограничений , где - известная матрица, а - известный вектор .

Применим метод множителей Лагранжа. Рассмотрим выражение: , где - вектор множителей Лагранжа. Решим уравнения:

(2.1)

(2.2)

Решения уравнений (2.1) и (2.2) обозначим через и 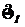. Тогда из (2.2) получаем:

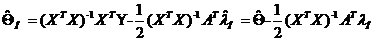, а из (2.1): .

Поскольку матрица - п.п.о., то матрица будет п.п.о. ранга . Следовательно

Окончательно подставляя в (2.3):

. (2.4)

Общая линейная гипотеза.

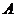Пусть мы хотим проверить гипотезу H: , где - известная матрица, - известный вектор. Обозначим: и , где 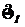нами вычислен в виде (2.4). Таким образом - минимальное значение при ограничениях .

Теорема 2.3.

3. Если гипотеза H верна, то статистика

(2.5) имеет распределение гипотеза H принимается если , где - критическая точка.

4. Если , то статистика принимает вид:

, где - симметричная и идемпотентная матрица и ,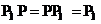

Частный случай: проверка значимости параметра H: или H: , где - вектор-строка, в которой на j-ом месте стоит 1, на остальных местах – нули. Обозначим - j-ый диагональный элемент.

Тогда: имеет при гипотезе H распределение .

Оценивание параметров в условиях мультиколлинеарности. Метод главных компонент.

Первой главной компонентой исследуемой системы показателей 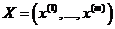называется такая нормировано-центрированная линейная комбинация этих показателей, которая среди всех прочих нормировано-центрированных линейных комбинаций переменных обладает наибольшей дисперсией.

k-ой главной компонентой исследуемой системы показателей 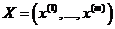называется такая нормировано-центрированная линейная комбинация этих показателей, которая не коррелированна с k-1 предыдущими главными компонентами и среди всех прочих нормировано-центрированных и некоррелированных с предыдущими k-1 главными компонентами линейных комбинаций переменных обладает наибольшей дисперсией.

Метод состоит в следующих преобразованиях и операциях:

1. Перейдем к центрированным наблюдениям 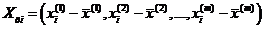, где и - количество факторов. Тогда

2. Уравнение регрессии по 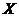в терминах центрированных переменных и примет вид , так что свободный член из исходного уравнения может быть выражен в виде , где и .

3. Определяем и упорядочиваем по убыванию собственные числа и соответствующие им собственные векторы матрицы .

4. Составляется матрица коэффициентов преобразования

, в которой -ый собственный вектор играет роль -ой строки. Отметим, что из построения следует, что матрица ортогональна, т.е. и .

5. С помощью матрицы переходим к вектору главных компонент

. Соответственно -ое наблюдение вектора главных компонент определяется соотношением , а матрица наблюдений главных компонент – соотношением

Отметим, что из построения следует:

и соответственно .

6. Возвращаемся к задаче регрессии и анализируем следующее:

В соответствии с основными соотношениями метода наименьших квадратов получаем:

С учетом того, что можно сделать вывод, что оценки взаимно некоррелированы и .

7. Обычно используют не все главные компоненты, а выбирают некоторые из них по определенному правилу. Обозначим множество индексов тех главных компонент, для которых выполняется следующее. Критерий информативности метода главных компонент может быть представлен в виде

, где - собственные числа ковариационной матрицы вектора 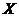, расположенные в порядке убывания. В множество поместим те индексы, которые не изменяют информативность при увеличении параметра .

8. Оценки для параметров получаются с учетом вышесказанных соотношений: и .

Вариант 5.

Методы оценивания параметров линейных регрессионных моделей.

Вычисление точечных оценок.

Наилучшие линейные оценки (НЛО) – оценки, обладающие свойствами состоятельности, несмещенности и эффективности (т.е. имеющие наименьшие дисперсии).

Вычисление оценок методом наименьших квадратов (МНК), который предполагает минимизацию суммы квадратов отклонений наблюдаемых значений отклика от их предсказанных значений.

Оценивание параметров регрессии по (ММП) методу максимального правдоподобия с помощью функции правдоподобия.

Доверительное оценивание.

Оценивание при наличии линейных ограничений.

Оценивание параметров регрессии в условиях повторных наблюдений.

Оценивание параметров регрессии в условиях мультиколлинеарности.

Для чего используется процедура Хилдрета Лу?

Для оценивания параметров модели при неизвестном .

Какие меры измерения эффекта мультиколлинеарности свободны от влияния масштаба.

Максимальная парная сопряженность: В качестве меры мультиколлинеарности выступает величина .

К каким последствиям приводят те или иные ошибки спецификации модели.

Ошибка перебора регрессоров или их недобора:

Точность оценивания при переборе теряется. Матрица ковариаций МНК оценки 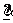для истинной модели равна , а матрица ковариаций оценки равна:

. (*)

Матрица F неотрицательно определена, так как , где - симметричная идемпотентная, а значит, и неотрицательно определённая матрица. Неотрицательная определённость F влечёт неотрицательную определённость второго слагаемого в (*), то есть . В случае же недобора оценка МНК является смещённой и несостоятельной.

Если наблюдений не очень много, то какой критерий качества моделей целесообразно использовать при выборе модели оптимальной сложности.

Когда исходная выборка не очень велика можно применить критерий скользящего контроля (прогноза). Из выборки объема n удаляется i-ый элемент , а по остальным (n-1) элементам строится оценка коэффициентов, которую мы обозначим . Затем определяется квадрат ошибки в i-ой точке , не использованной при оценке . Эта процедура повторяется n раз для каждого i=1,2,…,n, и результат усредняется.

Найдите оценку неизвестной дисперсии наблюдения по методу ММП.

Пусть - случайная выборка c известной функцией плотности, характеризующейся параметром . Функция правдоподобия наблюдаемых при заданных (или 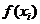) есть

Для упрощения возьмем (непрерывное преобразование не меняет экстремальные свойства функции)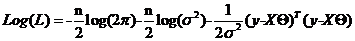

с неизвестными параметрами и . Для получения ММП оценок для необходимо решить.

Получили оценку для , т.е. , которая является смещенной однако она является сходящейся и асимптотически не смещенной при ® ¥.

Покажите, что Ридж оценка параметров линейной регрессионной модели является линейным преобразованием МНК оценки.

Выбор наилучшей модели. «Недобор» и «перебор» регрессоров. Показать выкладками.

Пусть параметрическое множество определяется функцией следующего вида , (4.1), где 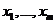- полный набор всех возможных регрессоров, содержащий такие функции как сами независимые переменные, квадраты, смешанные произведения, а так же все другие функции, которые кажутся подходящими. И пусть , причём в этом случае некоторые в (4.1) равны нулю. Другими словами, накрывает с перебором по числу ненулевых компонент в разложении (4.1). Вопрос состоит в том, какие именно регрессоры из 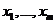следует включить в модель для получения наилучшей аппроксимации .

Случай перебора:

Пусть истинная модель есть , , (4.2) или , , . Вектор - неизвестные истинные параметры. Мы предполагаем, что

, (4.3) или , , .

МНК оценкой вектора в (4.3) является оценка , .

Докажем, что несмещённо оценивает . Другими словами, что , .

Обозначим . Тогда по формуле обращения блочных матриц

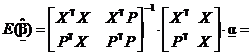
что доказывает несмещённость .

Можно показать, что оценка остаётся также и состоятельной оценкой для .

Случай недобора.

Пусть истинное уравнение (4.2), а мы оцениваем регрессию (4.5)

или , ,

Другими словами, , …, входят в регрессию (4.5), а остальные переменных , …, в регрессии отсутствуют.

Докажем, что тогда используемая оценка (4.6)

в общем случае является смещённой.

Действительно, ,

где и - подвекторы вектора размерности k и соответственно.

Перемножая, получим

Оценка будет несмещённой, когда матрицы W и V ортогональны, то есть .

Можно показать также, что МНК оценка в случае недобора является несостоятельной.

Несмещенное оценивание неизвестной дисперсии. Ошибки наблюдения.

Пусть модель объекта подчиняется следующему уравнению наблюдения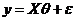

где y - вектор ненаблюдаемого незашумленного выхода объекта,

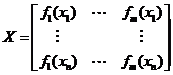- pасшиpенная матрица плана, соответствующая истинному набору pегpессоpов, - вектор ненаблюдаемых случайных ошибок измерения, относительно которых выполнены предположения: A1: ; A2: ;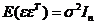

где 0− вектоp, состоящий из нулей, − неизвестная дисперсия наблюдения.

В критерии скользящего контроля определяется квадрат ошибки в i-ой точке , и результат усредняется , где . По величине можно найти оценку для неизвестной дисперсии наблюдения . Известно, что . Поэтому несмещенная оценка для будет вычисляться по формуле .

Вариант 6.

Что понимается под термином «структура» модели?
Общий вид модели, класс функций, к которым принадлежит модель.

Опишите в общих чертах многорядный комбинаторный алгоритм.
На первом шаге выбирается некоторое число лучших моделей, состоящих из одного регрессора. На втором этапе к этим моделям добавляются различные регрессоры по одному, и отбираются модели с двумя аргументами, улучшающие величину критерия, и т.д. до его ухудшения или до построения полной модели.

На последнем шаге можно из оставшихся лучших моделей выбрать одну по другому критерию. В алгоритме также можно эффективно использовать процедуру выметания.

В каких целях используется тест Дарбина-Уотсона?
Для проверки данных на наличие автокорреляции
Перечислите критерии качества моделей, основанные на использовании одной выборки.
MSEP-критерий, AEV-критерий, Множественный критерий корреляции.
Что такое «счетчик Гарсайда» и для чего он используется?
Это название последовательности выметаний для процедуры построения всех возможных моделей. Эта последовательность состоит из членов.
Как проверить значимость параметра линейной регрессионной модели?
Проверка осуществляется с помощью общей линейной гипотезы, гипотеза имеет вид . При справедливой гипотезе статистика , где , имеет распределение .

7. Проверка структурных изменений.
Пусть имеется две выборки ( - наблюдений) и ( - наблюдений). Нулевая гипотеза против альтернативы

Объединяя вместе две регрессии, получим: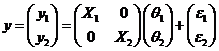

В нульгипотезе система ограничений на параметры будет:

F- статистика: , где – оценки вектора ошибок наблюдения с ограничением _.Важным специальным случаем является ситуация когда одна из выборок мала для того чтобы оценить по ней все параметры, параметр n₂= n – n₁< m. Тогда 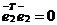. В этом случае соответствующая статистика имеет вид: .

Дата добавления: 2018-08-06; просмотров: 359; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 45

Мы поможем в написании ваших работ!